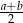Punkt 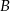 jest rzutem prostopadłym punktu
jest rzutem prostopadłym punktu 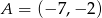 na prostą o równaniu
na prostą o równaniu 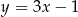 . Wskaż równanie prostej
. Wskaż równanie prostej 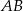 .
.
A) 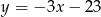 B)
B) 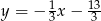 C)
C) 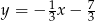 D)
D) 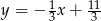
/Szkoła średnia/Zadania testowe/Geometria
Punkty 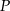 i
i 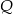 są środkami boków
są środkami boków 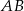 i
i 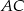 trójkąta
trójkąta 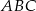 . Bok
. Bok 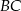 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu 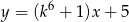 , a punkty
, a punkty 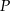 i
i 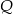 leżą na prostej
leżą na prostej 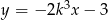 . Wynika stąd, że
. Wynika stąd, że
A) 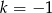 B)
B) 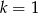 C)
C) 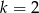 D)
D) 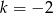
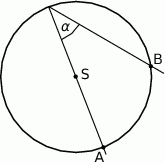
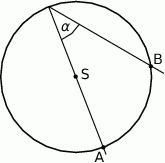
Na rysunku przedstawiono okrąg o środku 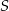 i kąt wpisany o mierze
i kąt wpisany o mierze 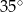 .
.
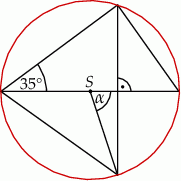
Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 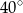 B)
B) 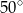 C)
C) 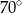 D)
D) 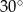
Środek okręgu o promieniu 10 jest oddalony od cięciwy 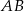 tego okręgu o 6. Długość tej cięciwy jest równa
tego okręgu o 6. Długość tej cięciwy jest równa
A) 10 B) 12 C) 14 D) 16
Środek okręgu o promieniu 5 jest oddalony od cięciwy 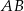 tego okręgu o 3. Długość tej cięciwy jest równa
tego okręgu o 3. Długość tej cięciwy jest równa
A) 5 B) 6 C) 7 D) 8
Przekątne trapezu 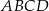 , w którym
, w którym 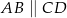 przecinają się w punkcie
przecinają się w punkcie 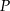 w ten sposób, że
w ten sposób, że 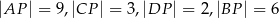 oraz
oraz 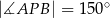 . Pole tego trapezu jest równe
. Pole tego trapezu jest równe
A) 32 B) 24 C) 18 D) 16
Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem 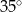 . Miara kąta rozwarcia stożka jest równa
. Miara kąta rozwarcia stożka jest równa
A) 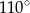 B)
B) 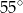 C)
C) 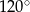 D)
D) 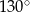
Punkty 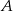 i
i 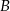 dzielą okrąg na dwa łuki, przy czym miary kątów wpisanych opartych na tych łukach różnią się o
dzielą okrąg na dwa łuki, przy czym miary kątów wpisanych opartych na tych łukach różnią się o 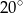 . Wynika stąd, że większy z tych katów ma miarę
. Wynika stąd, że większy z tych katów ma miarę
A) 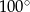 B)
B) 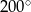 C)
C) 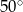 D)
D) 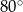
Wysokość trójkąta równobocznego o długości boku 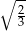 wynosi
wynosi
A) 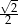 B)
B) 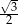 C)
C) 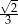 D)
D) 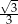
Pole koła opisanego na trójkącie równobocznym jest równe 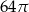 . Wysokość tego trójkąta ma długość
. Wysokość tego trójkąta ma długość
A) 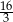 B) 16 C) 12 D) 24
B) 16 C) 12 D) 24
W kartezjańskim układzie współrzędnych 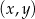 dane są proste
dane są proste 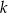 oraz
oraz 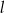 o równaniach
o równaniach
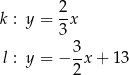
Proste 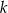 oraz
oraz 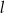
| A) są prostopadłe | B) nie są prostopadłe |
i przecinają się w punkcie 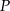 o współrzędnych
o współrzędnych
1. 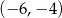 | 2. 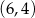 | 3. 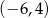 |
W kartezjańskim układzie współrzędnych 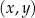 dane są proste
dane są proste 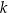 oraz
oraz 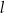 o równaniach
o równaniach
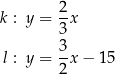
Proste 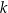 oraz
oraz 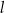
| A) są prostopadłe | B) nie są prostopadłe |
i przecinają się w punkcie 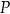 o współrzędnych
o współrzędnych
1. 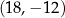 | 2. 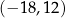 | 3. 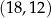 |
Dany jest trójkąt prostokątny (patrz rysunek).
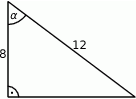
Wartość wyrażenia 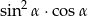 wynosi
wynosi
A) 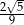 B)
B)  C)
C) 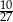 D)
D) 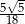
Dany jest trójkąt o bokach długości 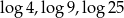 . Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
. Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
A) 2, 3, 5 B) 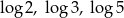 C)
C) 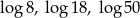 D) 4, 9, 25
D) 4, 9, 25
Stosunek długości trzech krawędzi prostopadłościanu o objętości 240 jest równy 2:3:5. Pole powierzchni tego prostopadłościanu jest równe:
A) 124 B) 248 C) 496 D) 62
Dany jest romb o boku długości  i dłuższej przekątnej długości
i dłuższej przekątnej długości 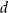 . Kąt rozwarty tego rombu ma miarę
. Kąt rozwarty tego rombu ma miarę 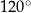 (zobacz rysunek).
(zobacz rysunek).
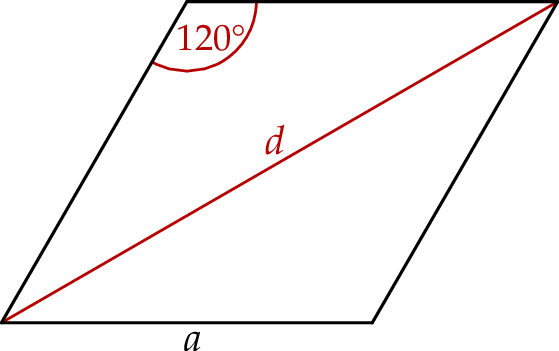
Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A–F. Pole tego rombu poprawnie określa wyrażenie
A) 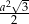 B)
B) 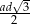 C)
C) 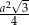
D) 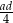 E)
E) 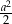 F)
F) 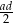
Które z poniższych zdań nie jest prawdziwe?
A) Na każdym prostokącie można opisać okrąg.
B) W każdy romb można wpisać okrąg.
C) Na każdym równoległoboku można opisać okrąg.
D) W każdy deltoid można wpisać okrąg.
Które z poniższych zdań nie jest prawdziwe?
A) W każdy romb można wpisać okrąg.
B) W każdy prostokąt można wpisać okrąg.
C) Na każdym prostokącie można opisać okrąg.
D) W każdy deltoid można wpisać okrąg.
Dany jest trapez 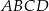 , w którym
, w którym 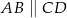 oraz przekątne
oraz przekątne 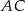 i
i 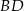 przecinają się w punkcie
przecinają się w punkcie 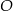 . Wysokość tego trapezu jest równa 12. Obwód trójkąta
. Wysokość tego trapezu jest równa 12. Obwód trójkąta 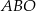 jest równy 39, a obwód trójkąta
jest równy 39, a obwód trójkąta 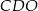 jest równy 13.
jest równy 13.
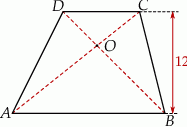
Wysokość trójkąta 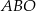 poprowadzona z punktu
poprowadzona z punktu 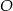 jest równa
jest równa
A) 3 B) 4 C) 9 D) 6
Dany jest trapez 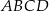 , w którym
, w którym 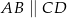 oraz przekątne
oraz przekątne 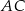 i
i 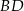 przecinają się w punkcie
przecinają się w punkcie 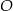 . Wysokość tego trapezu jest równa 15. Obwód trójkąta
. Wysokość tego trapezu jest równa 15. Obwód trójkąta 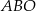 jest równy 42, a obwód trójkąta
jest równy 42, a obwód trójkąta 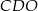 jest równy 14.
jest równy 14.
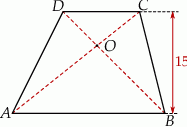
Wysokość trójkąta 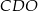 poprowadzona z punktu
poprowadzona z punktu 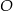 jest równa
jest równa
A) 3,75 B) 5 C) 6 D) 7,5
Punkt 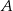 przesunięto o wektor
przesunięto o wektor ![[ 13 19] − 2 , 2](https://img.zadania.info/zad/7013744/HzadT1x.gif) i otrzymano punkt
i otrzymano punkt 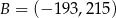 . Zatem
. Zatem
A) 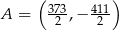 B)
B) 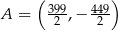 C)
C) 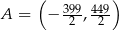 D)
D) 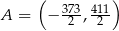
Dany jest okrąg o środku 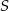 i promieniu
i promieniu  , długość łuku
, długość łuku 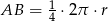 (patrz rysunek).
(patrz rysunek).
Miara kąta  jest równa
jest równa
A) 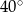 B)
B) 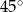 C)
C) 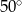 D)
D) 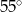
Dany jest okrąg o środku 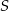 i promieniu
i promieniu  , długość łuku
, długość łuku 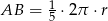 (patrz rysunek).
(patrz rysunek).
Miara kąta  jest równa
jest równa
A) 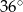 B)
B) 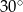 C)
C) 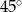 D)
D) 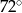
Boki równoległoboku mają długość 8 cm i 10 cm, a jego pole wynosi 40 cm. Kąt ostry równoległoboku ma miarę:
A) 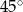 B)
B) 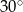 C)
C) 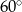 D)
D) 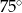
Boki równoległoboku mają długości: 6 cm i 10 cm, a jego pole wynosi 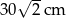 . Kąt ostry równoległoboku ma miarę:
. Kąt ostry równoległoboku ma miarę:
A) 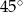 B)
B) 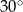 C)
C) 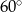 D)
D) 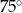
Długości podstaw trapezu wynoszą  oraz
oraz 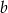 , gdzie
, gdzie 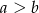 . Zatem odcinek, którego końcami są środki ramion trapezu, ma długość
. Zatem odcinek, którego końcami są środki ramion trapezu, ma długość
A) 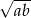 B)
B) 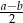 C)
C) 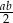 D)
D)