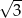Punkt 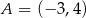 jest końcem odcinka
jest końcem odcinka 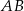 , a punkt
, a punkt 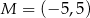 jest takim punktem tego odcinka, że
jest takim punktem tego odcinka, że 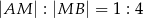 . Długość odcinka
. Długość odcinka 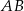 jest równa
jest równa
A) 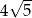 B)
B) 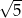 C)
C) 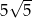 D)
D) 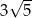
/Szkoła średnia/Zadania testowe/Geometria
Punkt 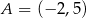 jest końcem odcinka
jest końcem odcinka 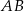 , a punkt
, a punkt 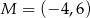 jest takim punktem tego odcinka, że
jest takim punktem tego odcinka, że 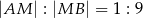 . Długość odcinka
. Długość odcinka 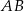 jest równa
jest równa
A) 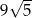 B)
B) 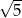 C)
C) 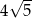 D)
D) 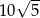
Punkty 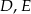 i
i 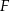 są środkami krawędzi
są środkami krawędzi 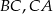 i
i 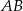 podstawy
podstawy 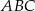 ostrosłupa trójkątnego
ostrosłupa trójkątnego 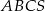 . Stosunek objętości ostrosłupa
. Stosunek objętości ostrosłupa 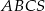 do objętości ostrosłupa
do objętości ostrosłupa 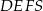 jest równy
jest równy
A) 4 B) 8 C) 3 D) 9
Dany jest sześciokąt foremny 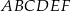 o polu równym
o polu równym 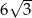 (zobacz rysunek).
(zobacz rysunek).
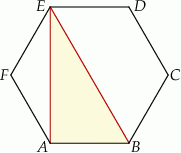
Długość odcinka 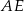 jest równa
jest równa
A) 2 B) 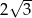 C)
C) 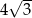 D) 4
D) 4
Długości boków trójkąta są liczbami całkowitymi. Jeden bok ma 7 cm, a drugi ma 2 cm. Trzeci bok tego trójkąta może mieć długość
A) 12 cm B) 9 cm C) 6 cm D) 3 cm
Długości boków trójkąta są liczbami całkowitymi. Jeden bok ma 4 cm, a drugi ma 9 cm. Trzeci bok tego trójkąta może mieć długość
A) 4 cm B) 5 cm C) 14 cm D) 9 cm
Punkty 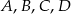 leżą na okręgu w podanej kolejności. Cięciwy
leżą na okręgu w podanej kolejności. Cięciwy 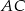 i
i 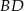 przecinają się w punkcie
przecinają się w punkcie 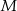 . Zatem
. Zatem
A) 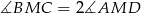 B)
B) 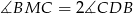 C)
C) 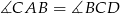 D)
D) 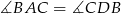
Punkty 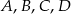 leżą na okręgu w podanej kolejności. Cięciwy
leżą na okręgu w podanej kolejności. Cięciwy 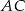 i
i 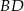 przecinają się w punkcie
przecinają się w punkcie 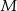 . Zatem
. Zatem
A) 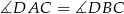 B)
B) 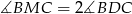 C)
C) 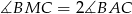 D)
D) 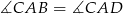
Punkty 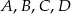 leżą na okręgu w podanej kolejności. Cięciwy
leżą na okręgu w podanej kolejności. Cięciwy 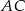 i
i 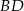 przecinają się w punkcie
przecinają się w punkcie 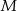 . Zatem
. Zatem
A) 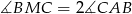 B)
B) 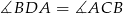 C)
C) 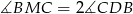 D)
D) 
Na końcowym ramieniu kąta  (rysunek) leży punkt
(rysunek) leży punkt 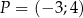 .
.
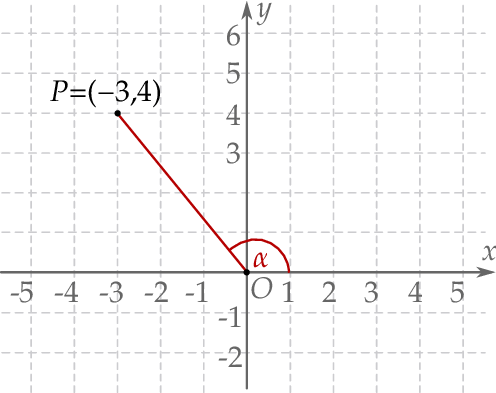
Wówczas
A) 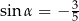 B)
B) 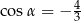 C)
C) 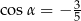 D)
D) 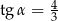
Punkt 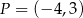 leży na końcowym ramieniu kąta
leży na końcowym ramieniu kąta  . Cosinus kąta
. Cosinus kąta  jest równy
jest równy
A)  B)
B) 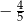 C)
C)  D)
D) 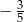
Punkty 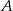 ,
, 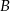 i
i 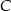 leżą na okręgu o środku
leżą na okręgu o środku 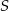 , a prosta
, a prosta 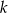 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 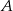 .
.
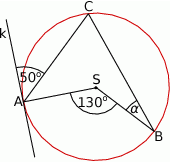
Zaznaczony na rysunku kąt  zawarty między promieniem
zawarty między promieniem 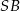 i cięciwą
i cięciwą 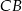 ma miarę
ma miarę
A) 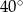 B)
B) 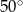 C)
C) 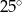 D)
D) 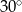
Dany jest ostrosłup, którego podstawą jest kwadrat o boku 5. Jedna z krawędzi bocznych tego ostrosłupa ma długość 9 i jest prostopadła do płaszczyzny podstawy. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Każda ze ścian bocznych ostrosłupa jest trójkątem prostokątnym. | P | F |
Cosinus kąta nachylenia najdłuższej krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy jest równy 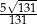 . . | P | F |
Jeżeli trójkąty 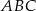 i
i 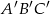 są podobne, a ich obwody są odpowiednio równe 25 cm i 50 cm, to skala podobieństwa trójkątów
są podobne, a ich obwody są odpowiednio równe 25 cm i 50 cm, to skala podobieństwa trójkątów 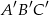 i
i 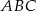 jest równa
jest równa
A) 2 B) 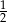 C)
C) 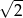 D)
D) 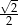
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 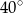 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 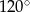 B)
B) 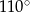 C)
C) 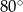 D)
D) 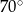
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 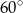 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 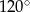 B)
B) 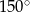 C)
C) 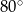 D)
D) 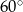
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 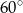 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 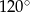 B)
B) 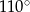 C)
C) 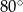 D)
D) 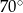
Trójkąt prostokątny 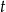 obrócono względem dłuższej przyprostokątnej i otrzymano stożek o polu powierzchni bocznej
obrócono względem dłuższej przyprostokątnej i otrzymano stożek o polu powierzchni bocznej 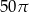 i kącie rozwarcia
i kącie rozwarcia 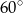 . Obwód trójkąta
. Obwód trójkąta 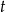 jest równy
jest równy
A) 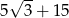 B)
B) 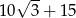 C)
C) 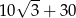 D)
D) 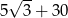
Przekrój osiowy walca jest kwadratem o boku długości 8. Pole powierzchni bocznej tego walca jest równe:
A) 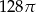 B)
B) 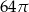 C)
C) 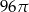 D)
D) 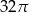
Przekrój osiowy walca jest kwadratem o przekątnej 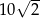 . Pole powierzchni bocznej tego walca jest równe:
. Pole powierzchni bocznej tego walca jest równe:
A) 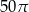 B)
B) 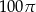 C)
C) 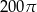 D)
D) 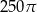
Pole równoległoboku o bokach długości 6 i 8 oraz kącie rozwartym 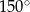 jest równe
jest równe
A) 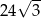 B) 48 C)
B) 48 C) 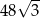 D) 24
D) 24
Boki równoległoboku mają długości 6 i 10, a kąt rozwarty między tymi bokami ma miarę 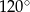 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 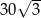 B) 30 C)
B) 30 C) 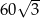 D) 60
D) 60
Dany jest równoległobok o bokach długości 3 i 4 oraz o kącie między nimi o mierze 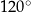 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 12 B) 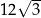 C) 6 D)
C) 6 D) 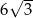
Pole równoległoboku o bokach długości 4 i 7 oraz kącie rozwartym 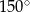 jest równe
jest równe
A) 14 B) 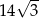 C)
C) 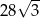 D) 28
D) 28
Pole równoległoboku o bokach długości 6 cm i 10 cm i kącie rozwartym o mierze 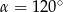 jest równe
jest równe
A) 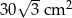 B)
B) 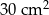 C)
C) 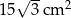 D)
D) 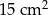
Różnica miar dwóch kątów rozwartych trapezu jest równa 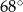 . Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
. Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
A) 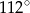 B)
B) 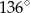 C)
C) 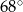 D)
D) 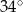
Pole trójkąta równobocznego wpisanego w koło o polu 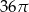 jest równe
jest równe
A) 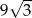 B) 81 C)
B) 81 C) 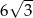 D)
D) 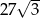
Dane są długości boków 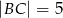 i
i 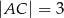 trójkąta prostokątnego
trójkąta prostokątnego 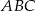 o kącie ostrym
o kącie ostrym 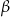 (zobacz rysunek).
(zobacz rysunek).
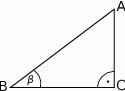
Wtedy
A) 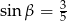 B)
B) 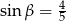 C)
C) 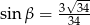 D)
D) 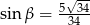
W trójkącie, przedstawionym na rysunku poniżej, sinus kąta ostrego  jest równy
jest równy
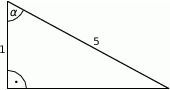
A) 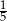 B)
B) 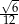 C)
C) 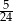 D)
D) 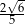
W trójkącie prostokątnym 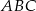 przyprostokątne mają długość
przyprostokątne mają długość 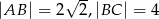 , a kąt
, a kąt 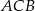 ma miarę
ma miarę  .
.
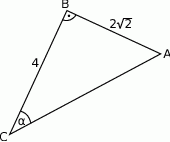
Zatem
A) 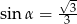 B)
B) 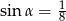 C)
C) 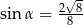 D)
D) 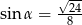
W trójkącie prostokątnym 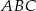 przyprostokątne mają długość
przyprostokątne mają długość 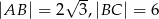 , a kąt
, a kąt 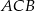 ma miarę
ma miarę  .
.
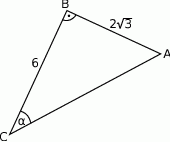
Zatem
A) 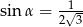 B)
B) 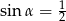 C)
C) 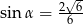 D)
D) 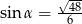
W trójkącie prostokątnym 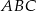 przyprostokątne mają długość
przyprostokątne mają długość 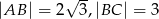 , a kąt
, a kąt 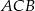 ma miarę
ma miarę  .
.
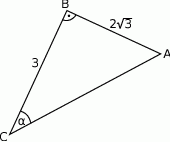
Zatem
A) 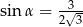 B)
B) 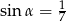 C)
C) 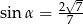 D)
D) 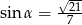
W trójkącie, przedstawionym na rysunku poniżej, cosinus kąta ostrego  jest równy
jest równy
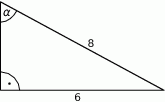
A)  B)
B)  C)
C) 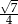 D)
D) 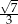
Dane są długości boków 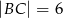 i
i 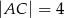 trójkąta prostokątnego
trójkąta prostokątnego 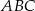 o kącie ostrym
o kącie ostrym 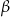 (zobacz rysunek).
(zobacz rysunek).
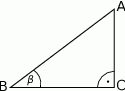
Wtedy
A) 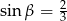 B)
B) 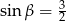 C)
C) 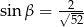 D)
D) 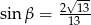
Dany jest prostopadłościan o krawędziach długości  ,
, 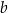 i
i  , gdzie
, gdzie 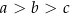 . Suma długości wszystkich krawędzi tego prostopadłościanu jest równa 116. Pole powierzchni całkowitej prostopadłościanu jest równe 552. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
. Suma długości wszystkich krawędzi tego prostopadłościanu jest równa 116. Pole powierzchni całkowitej prostopadłościanu jest równe 552. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Zależności między długościami krawędzi tego prostopadłościanu zapisano w układzie równań
A) 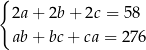 B)
B) 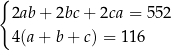 C)
C) 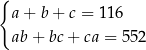
D) 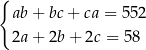 E)
E) 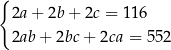 F)
F) 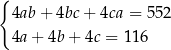
Pole trójkąta 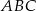 jest cztery razy mniejsze od pola trójkąta
jest cztery razy mniejsze od pola trójkąta 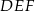 . Trójkąty te są podobne. Długość boku
. Trójkąty te są podobne. Długość boku 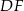 jest równa 16. Długość boku
jest równa 16. Długość boku 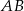 , odpowiadającego bokowi
, odpowiadającego bokowi 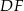 , jest równa
, jest równa
A) 64 B) 32 C) 4 D) 8
Trójkąty 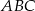 i
i 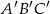 są podobne
są podobne 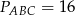 ,
, 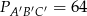 , wysokość
, wysokość 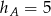 . Odpowiadająca jej wysokość w drugim trójkącie jest równa:
. Odpowiadająca jej wysokość w drugim trójkącie jest równa:
A) 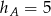 B)
B) 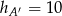 C)
C) 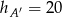 D) nie można określić
D) nie można określić
Pole trójkąta 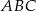 jest dziewięć razy mniejsze od pola trójkąta
jest dziewięć razy mniejsze od pola trójkąta 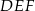 . Trójkąty te są podobne. Długość boku
. Trójkąty te są podobne. Długość boku 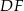 jest równa 9. Długość boku
jest równa 9. Długość boku 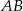 , odpowiadającego bokowi
, odpowiadającego bokowi 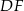 , jest równa
, jest równa
A) 81 B) 27 C) 3 D) 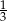
Pole trójkąta 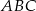 jest cztery razy większe od pola trójkąta
jest cztery razy większe od pola trójkąta 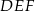 . Trójkąty te są podobne. Długość boku
. Trójkąty te są podobne. Długość boku 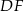 jest równa 16. Długość boku
jest równa 16. Długość boku 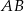 , odpowiadającego bokowi
, odpowiadającego bokowi 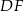 , jest równa
, jest równa
A) 64 B) 32 C) 4 D) 8
Przekrój osiowy stożka jest trójkątem o polu 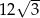 . Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem
. Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 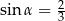 . Pole powierzchni bocznej tego stożka jest równe
. Pole powierzchni bocznej tego stożka jest równe
A) 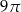 B)
B) 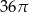 C)
C) 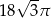 D)
D) 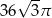
W trapezie prostokątnym kąt ostry ma miarę 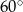 . Wysokość tego trapezu jest równa 3 cm. O ile centymetrów dłuższa jest jedna podstawa od drugiej?
. Wysokość tego trapezu jest równa 3 cm. O ile centymetrów dłuższa jest jedna podstawa od drugiej?
A) 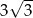 B) 6 C) 3 D)
B) 6 C) 3 D)