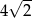Punkty 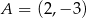 i
i 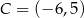 są wierzchołkami rombu
są wierzchołkami rombu 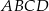 . Środkiem okręgu wpisanego w romb jest punkt
. Środkiem okręgu wpisanego w romb jest punkt
A) 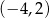 B)
B) 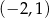 C)
C) 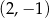 D)
D) 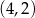
/Szkoła średnia/Zadania testowe/Geometria
Punkty 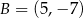 i
i 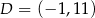 są wierzchołkami rombu
są wierzchołkami rombu 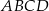 . Środkiem okręgu wpisanego w romb jest punkt
. Środkiem okręgu wpisanego w romb jest punkt
A) 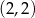 B)
B) 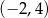 C)
C) 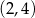 D)
D) 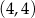
Punkty 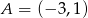 i
i 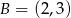 są kolejnymi wierzchołkami kwadratu. Obwód tego kwadratu jest równy
są kolejnymi wierzchołkami kwadratu. Obwód tego kwadratu jest równy
A) 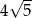 B)
B) 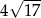 C)
C) 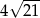 D)
D) 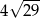
Punkty 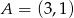 i
i 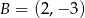 są kolejnymi wierzchołkami kwadratu. Obwód tego kwadratu jest równy
są kolejnymi wierzchołkami kwadratu. Obwód tego kwadratu jest równy
A) 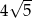 B)
B) 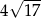 C)
C) 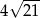 D)
D) 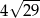
Dane są dwa okręgi o promieniach 12 i 17. Mniejszy okrąg przechodzi przez środek większego okręgu. Odległość między środkami tych okręgów jest równa
A) 5 B) 12 C) 17 D) 29
Dane są dwa okręgi o promieniach 10 i 15. Mniejszy okrąg przechodzi przez środek większego okręgu. Odległość między środkami tych okręgów jest równa
A) 2,5 B) 5 C) 10 D) 12,5
Dane są dwa okręgi o promieniach 10 i 18. Większy okrąg przechodzi przez środek mniejszego okręgu. Odległość między środkami tych okręgów jest równa
A) 18 B) 8 C) 10 D) 28
Dane są dwa okręgi o promieniach 12 i 17. Większy okrąg przechodzi przez środek mniejszego okręgu. Odległość między środkami tych okręgów jest równa
A) 5 B) 12 C) 17 D) 29
Kąty wewnętrzne przy wierzchołkach 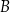 i
i 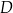 trapezu
trapezu 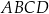 są równe odpowiednio
są równe odpowiednio 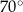 i
i 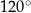 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 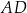 i
i 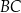 przecinają się pod kątem
przecinają się pod kątem
A) 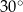 B)
B) 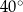 C)
C) 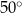 D)
D) 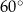
Kąty wewnętrzne przy wierzchołkach 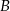 i
i 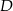 trapezu
trapezu 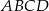 są równe odpowiednio
są równe odpowiednio 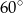 i
i 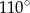 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 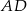 i
i 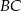 przecinają się pod kątem
przecinają się pod kątem
A) 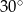 B)
B) 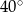 C)
C) 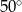 D)
D) 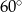
W okręgu o środku w punkcie 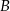 kąt środkowy
kąt środkowy  i kąt wpisany
i kąt wpisany 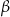 oparte są na tym samym łuku wyznaczonym przez punkty
oparte są na tym samym łuku wyznaczonym przez punkty 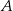 i
i 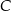 leżące na okręgu. Suma miar tych kątów jest równa kątowi prostemu. Wierzchołek kąta
leżące na okręgu. Suma miar tych kątów jest równa kątowi prostemu. Wierzchołek kąta 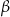 znajduje się w punkcie
znajduje się w punkcie 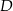 . Wynika stąd, że trójkąt
. Wynika stąd, że trójkąt
A) 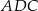 jest równoboczny B)
jest równoboczny B) 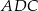 jest prostokątny
jest prostokątny
C) 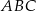 jest równoboczny D)
jest równoboczny D) 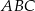 jest prostokątny
jest prostokątny
W okręgu o środku w punkcie 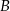 kąt środkowy
kąt środkowy  i kąt wpisany
i kąt wpisany 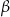 oparte są na tym samym łuku wyznaczonym przez punkty
oparte są na tym samym łuku wyznaczonym przez punkty 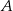 i
i 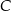 leżące na okręgu. Suma miar tych kątów jest równa
leżące na okręgu. Suma miar tych kątów jest równa 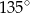 . Wierzchołek kąta
. Wierzchołek kąta 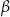 znajduje się w punkcie
znajduje się w punkcie 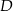 . Wynika stąd, że trójkąt
. Wynika stąd, że trójkąt
A) 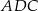 jest równoboczny B)
jest równoboczny B) 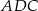 jest prostokątny
jest prostokątny
C) 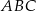 jest równoboczny D)
jest równoboczny D) 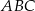 jest prostokątny
jest prostokątny
W okręgu o środku w punkcie 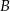 kąt środkowy
kąt środkowy  i kąt wpisany
i kąt wpisany 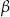 oparte są na tym samym łuku wyznaczonym przez punkty
oparte są na tym samym łuku wyznaczonym przez punkty 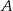 i
i 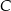 leżące na okręgu. Różnica miar tych kątów jest równa
leżące na okręgu. Różnica miar tych kątów jest równa 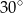 . Wierzchołek kąta
. Wierzchołek kąta 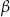 znajduje się w punkcie
znajduje się w punkcie 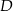 . Wynika stąd, że trójkąt
. Wynika stąd, że trójkąt
A) 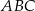 jest równoboczny B)
jest równoboczny B) 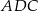 jest prostokątny
jest prostokątny
C) 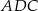 jest równoboczny D)
jest równoboczny D) 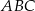 jest prostokątny
jest prostokątny
W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość 4, wysokość ostrosłupa ma długość 5. Ściana boczna jest nachylona do podstawy pod kątem  takim, że
takim, że
A) 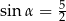 B)
B) 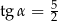 C)
C) 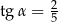 D)
D) 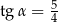
Podstawą ostrosłupa prawidłowego czworokątnego jest kwadrat o boku długości 4. Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod takim kątem  , że
, że 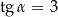 . Wysokość tego ostrosłupa jest równa
. Wysokość tego ostrosłupa jest równa
A) 3 B) 6 C) 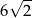 D) 12
D) 12
Odległość punktu 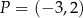 od prostej o równaniu
od prostej o równaniu 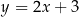 jest równa
jest równa
A) 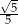 B)
B) 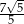 C)
C) 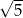 D) 5
D) 5
Odległość punktu 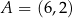 od prostej o równaniu
od prostej o równaniu 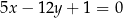 jest równa
jest równa
A) 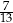 B)
B) 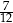 C)
C) 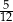 D)
D) 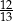
Punkty 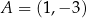 oraz
oraz 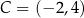 są końcami przekątnej
są końcami przekątnej 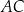 rombu
rombu 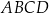 . Środek przekątnej
. Środek przekątnej 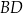 tego rombu ma współrzędne
tego rombu ma współrzędne
A) 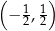 B)
B) 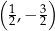 C)
C) 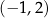 D)
D) 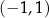
Bok 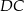 prostokąta
prostokąta 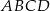 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 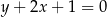 . Jedna z przekątnych tego prostokąta może być zawarta w prostej o równaniu
. Jedna z przekątnych tego prostokąta może być zawarta w prostej o równaniu
A) 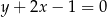 B)
B) 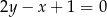 C)
C) 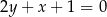 D)
D) 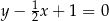
Stosunek pól dwóch kół jest równy 9. Wynika stąd, że promień większego koła jest większy od promienia mniejszego koła
A) o 9 B) o 3 C) 9 razy D) 3 razy
Stosunek pól dwóch kół jest równy 4. Wynika stąd, że promień większego koła jest większy od promienia mniejszego koła
A) o 4 B) 16 razy C) 2 razy D) 4 razy
Stosunek pól dwóch kół jest równy 16. Wynika stąd, że promień większego koła jest większy od promienia mniejszego koła
A) o 16 B) o 4 C) 4 razy D) 16 razy
Stosunek pól dwóch kół jest równy 9. Wynika stąd, że promień mniejszego koła jest mniejszy od promienia większego koła
A) 3 razy B) o 3 C) 9 razy D) o 9
Pięciokąt 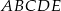 jest foremny. Wskaż trójkąt przystający do trójkąta
jest foremny. Wskaż trójkąt przystający do trójkąta 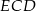
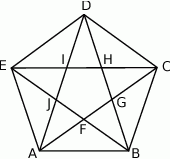
A) 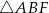 B)
B) 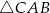 C)
C) 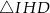 D)
D) 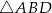
Pięciokąt 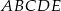 jest foremny. Wskaż trójkąt przystający do trójkąta
jest foremny. Wskaż trójkąt przystający do trójkąta 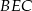
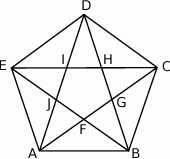
A) 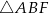 B)
B) 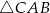 C)
C) 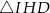 D)
D) 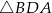
W trapezie prostokątnym krótsza podstawa i dłuższe ramię są równe i mają długość 8 cm. Kąt między dłuższym ramieniem i dłuższą podstawą ma miarę 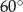 . Pole trapezu jest równe
. Pole trapezu jest równe
A) 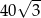 B)
B) 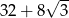 C) 40 D)
C) 40 D) 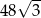
Punkty 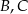 i
i 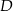 leżą na okręgu o środku
leżą na okręgu o środku 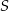 i promieniu
i promieniu  . Punkt
. Punkt 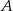 jest punktem wspólnym prostych
jest punktem wspólnym prostych 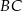 i
i 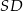 , a odcinki
, a odcinki 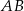 i
i 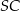 są równej długości. Miara kąta
są równej długości. Miara kąta 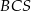 jest równa
jest równa 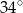 (zobacz rysunek). Wtedy
(zobacz rysunek). Wtedy
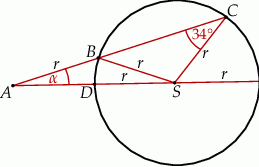
A) 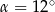 B)
B) 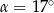 C)
C) 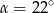 D)
D) 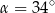
Punkty 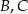 i
i 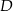 leżą na okręgu o środku
leżą na okręgu o środku 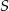 i promieniu
i promieniu  . Punkt
. Punkt 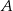 jest punktem wspólnym prostych
jest punktem wspólnym prostych 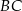 i
i 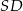 , a odcinki
, a odcinki 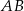 i
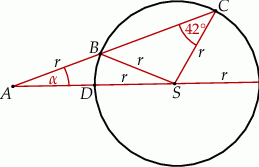
i 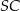 są równej długości. Miara kąta
są równej długości. Miara kąta 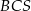 jest równa
jest równa 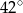 (zobacz rysunek). Wtedy
(zobacz rysunek). Wtedy
A) 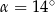 B)
B) 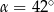 C)
C) 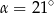 D)
D) 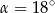
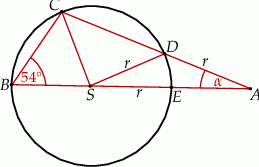
Punkty 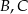 i
i 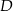 leżą na okręgu o środku
leżą na okręgu o środku 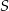 i promieniu
i promieniu  . Punkt
. Punkt 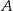 jest punktem wspólnym prostych
jest punktem wspólnym prostych 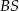 i
i 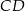 , a odcinki
, a odcinki 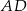 i
i 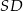 są równej długości. Miara kąta
są równej długości. Miara kąta 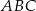 jest równa
jest równa 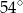 (zobacz rysunek). Wtedy
(zobacz rysunek). Wtedy
A) 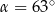 B)
B) 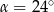 C)
C) 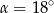 D)
D) 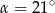
Pole trójkąta wyznaczonego przez wykresy funkcji 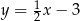 i
i 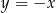 oraz oś
oraz oś 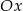 jest równe
jest równe
A) 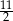 B)
B) 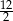 C)
C) 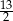 D)
D) 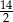
Pole trójkąta wyznaczonego przez wykresy funkcji 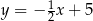 i
i 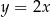 oraz oś
oraz oś 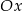 jest równe
jest równe
A) 20 B) 10 C) 32 D) 40
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 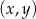 , dane są punkty
, dane są punkty 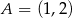 i
i 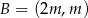 , gdzie
, gdzie 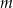 jest liczbą rzeczywistą, oraz prosta
jest liczbą rzeczywistą, oraz prosta 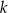 o równaniu
o równaniu 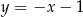 . Prosta przechodząca przez punkty
. Prosta przechodząca przez punkty 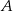 i
i 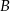 jest prostopadła do prostej
jest prostopadła do prostej 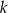 , gdy
, gdy
A) 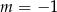 B)
B) 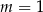 C)
C) 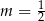 D)
D) 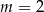
Kąt rozwarcia stożka ma miarę 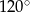 , a jego tworząca ma długość 10. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
, a jego tworząca ma długość 10. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
A) 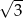 B)
B) 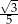 C) 5 D)
C) 5 D) 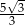
Kąt rozwarcia stożka ma miarę 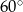 , a jego tworząca ma długość 8. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
, a jego tworząca ma długość 8. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
A) 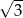 B)
B) 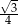 C)
C) 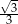 D)
D) 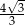
Kąt rozwarcia stożka ma miarę 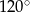 , a jego tworząca ma długość 12. Wówczas stosunek wysokości stożka do jego promienia podstawy jest równy
, a jego tworząca ma długość 12. Wówczas stosunek wysokości stożka do jego promienia podstawy jest równy
A) 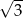 B)
B) 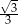 C)
C) 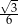 D)
D) 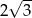
W graniastosłupie prawidłowym sześciokątnym 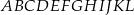 wierzchołki
wierzchołki 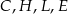 połączono odcinkami (tak jak na rysunku).
połączono odcinkami (tak jak na rysunku).
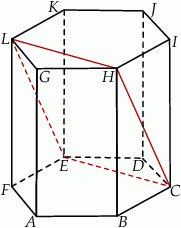
Wskaż kąt między bokiem 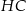 czworokąta
czworokąta 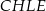 i płaszczyzną podstawy tego graniastosłupa.
i płaszczyzną podstawy tego graniastosłupa.
A) 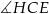 B)
B) 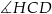 C)
C) 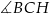 D)
D) 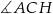
Liczba krawędzi graniastosłupa jest o 10 większa od liczby jego ścian. Ile wierzchołków ma ten graniastosłup?
A) 6 B) 18 C) 24 D) 12
Liczba krawędzi graniastosłupa jest o 8 większa od liczby jego ścian. Ile wierzchołków ma ten graniastosłup?
A) 5 B) 15 C) 10 D) 16
Liczba wszystkich krawędzi graniastosłupa jest o 10 większa od liczby wszystkich jego ścian bocznych. Stąd wynika, że podstawą tego graniastosłupa jest
A) czworokąt B) pięciokąt C) sześciokąt D) dziesięciokąt
Liczba wszystkich krawędzi graniastosłupa jest o 12 większa od liczby wszystkich jego ścian bocznych. Stąd wynika, że podstawą tego graniastosłupa jest
A) czworokąt B) pięciokąt C) sześciokąt D) dziesięciokąt
W trapezie prostokątnym podstawy mają długości 6 i 9. Która z liczb nie może być długością dłuższego ramienia trapezu?
A) 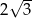 B)
B) 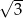 C)
C) 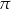 D)
D) 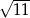
Kąt rozwarcia stożka ma miarę 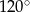 , a tworząca tego stożka ma długość 6. Promień podstawy stożka jest równy
, a tworząca tego stożka ma długość 6. Promień podstawy stożka jest równy
A) 3 B) 6 C) 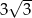 D)
D) 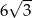
Kąt rozwarcia stożka ma miarę 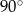 , a tworząca tego stożka ma długość 8. Promień podstawy stożka jest równy
, a tworząca tego stożka ma długość 8. Promień podstawy stożka jest równy
A) 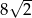 B) 4 C)
B) 4 C) 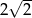 D)
D)