Dwa boki trójkąta 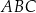 są zawarte w prostych
są zawarte w prostych 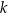 i
i 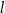 o równaniach
o równaniach
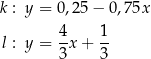
Trójkąt 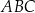
| A) jest prostokątny | B) nie jest prostokątny |
i jeden z jego wierzchołków może mieć współrzędne
1. 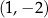 | 2. 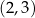 | 3.  |
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dwa boki trójkąta 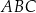 są zawarte w prostych
są zawarte w prostych 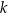 i
i 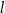 o równaniach
o równaniach
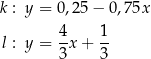
Trójkąt 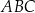
| A) jest prostokątny | B) nie jest prostokątny |
i jeden z jego wierzchołków może mieć współrzędne
1. 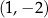 | 2. 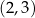 | 3.  |
W trójkącie równoramiennym o polu 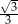 miara kąta przy podstawie jest równa
miara kąta przy podstawie jest równa 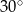 . Długość podstawy tego trójkąta jest liczbą
. Długość podstawy tego trójkąta jest liczbą
A) wymierną mniejszą od 2 B) niewymierną większą o 1
C) całkowitą większą od 1 D) niewymierną mniejszą od 2
W trójkącie równoramiennym o polu 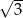 miara kąta przy podstawie jest równa
miara kąta przy podstawie jest równa 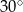 . Długość podstawy tego trójkąta jest liczbą
. Długość podstawy tego trójkąta jest liczbą
A) wymierną mniejszą od 3 B) niewymierną większą o 3
C) całkowitą większą od 3 D) niewymierną mniejszą od 3
W trójkącie równoramiennym o polu 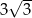 miara kąta przy podstawie jest równa
miara kąta przy podstawie jest równa 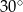 . Długość podstawy tego trójkąta jest liczbą
. Długość podstawy tego trójkąta jest liczbą
A) całkowitą większą od 4 B) niewymierną większą o 4
C) wymierną mniejszą od 4 D) niewymierną mniejszą od 4
Wysokość ściany bocznej ostrosłupa prawidłowego sześciokątnego jest 2 razy dłuższa od krawędzi jego podstawy. Stosunek pola powierzchni bocznej tego ostrosłupa do pola jego podstawy jest równy
A) 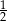 B)
B) 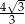 C) 1 D)
C) 1 D) 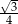
Wysokość ściany bocznej ostrosłupa prawidłowego sześciokątnego jest 3 razy dłuższa od krawędzi jego podstawy. Stosunek pola powierzchni bocznej tego ostrosłupa do pola jego podstawy jest równy
A) 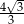 B)
B) 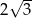 C)
C) 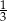 D)
D) 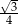
Punkty 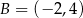 i
i 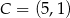 są dwoma sąsiednimi wierzchołkami kwadratu
są dwoma sąsiednimi wierzchołkami kwadratu 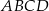 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 74 B) 58 C) 40 D) 29
Punkty 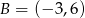 i
i 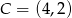 są dwoma sąsiednimi wierzchołkami kwadratu
są dwoma sąsiednimi wierzchołkami kwadratu 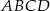 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 17 B) 113 C) 65 D) 29
Punkty 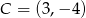 i
i 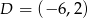 są dwoma sąsiednimi wierzchołkami kwadratu
są dwoma sąsiednimi wierzchołkami kwadratu 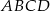 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 117 B) 85 C) 13 D) 45
Punkty 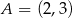 i
i 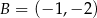 są sąsiednimi wierzchołkami kwadratu
są sąsiednimi wierzchołkami kwadratu 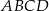 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 36 B) 30 C) 32 D) 34
Która z podanych prostych jest symetryczna do prostej 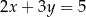 względem osi
względem osi 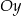 ?
?
A) 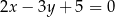 B)
B) 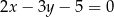 C)
C) 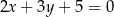 D)
D) 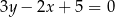
Która z podanych prostych jest symetryczna do prostej 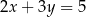 względem osi
względem osi 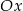 ?
?
A) 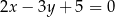 B)
B) 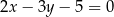 C)
C) 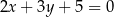 D)
D) 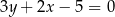
Na okręgu o równaniu 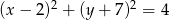 leży punkt
leży punkt
A) 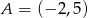 B)
B) 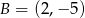 C)
C) 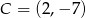 D)
D) 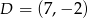
Do okręgu o równaniu 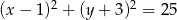 należy punkt
należy punkt
A) 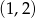 B)
B) 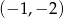 C)
C) 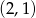 D)
D) 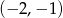
Na okręgu o równaniu 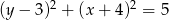 leży punkt
leży punkt
A) 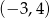 B)
B) 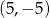 C)
C) 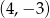 D)
D) 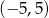
Pięć identycznych metalowych stożków o promieniu podstawy  przetopiono na jeden walec, którego wysokość jest równa
przetopiono na jeden walec, którego wysokość jest równa 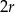 i jest dwa razy krótsza od jego promienia podstawy. Gdyby te same stożki przetopiono na kule o promieniu
i jest dwa razy krótsza od jego promienia podstawy. Gdyby te same stożki przetopiono na kule o promieniu  , to ile takich kul by otrzymano?
, to ile takich kul by otrzymano?
A) 32 B) 16 C) 8 D) 24
Wysokość 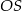 walca jest równa 2, a cosinus kąta
walca jest równa 2, a cosinus kąta 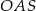 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy  .
.
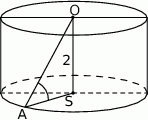
Pole powierzchni bocznej tego walca jest równe
A) 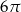 B)
B) 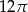 C)
C) 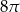 D)
D) 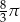
Jeżeli  oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
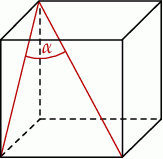
A) 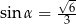 B)
B) 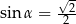 C)
C) 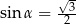 D)
D) 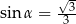
Dany jest sześcian  . Sinus kąta
. Sinus kąta  nachylenia przekątnej
nachylenia przekątnej 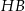 tego sześcianu do płaszczyzny podstawy
tego sześcianu do płaszczyzny podstawy  (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
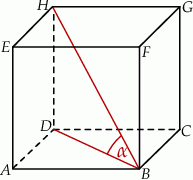
A) 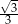 B)
B) 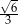 C)
C) 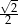 D)
D) 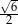
Jeżeli  oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
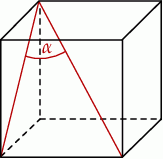
A) 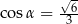 B)
B) 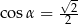 C)
C) 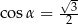 D)
D) 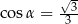
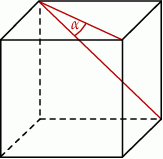
Jeżeli  oznacza miarę kąta między przekątnymi ścian sześcianu (zobacz rysunek), to
oznacza miarę kąta między przekątnymi ścian sześcianu (zobacz rysunek), to
A) 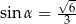 B)
B) 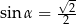 C)
C) 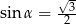 D)
D) 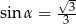
Zbiór punktów wspólnych kuli i prostej może być
A) zbiorem dwuelementowym B) zbiorem jednoelementowym C) okręgiem D) kołem
Zbiór punktów wspólnych kuli i płaszczyzny może być
A) zbiorem dwuelementowym B) okręgiem C) zbiorem jednoelementowym D) sferą
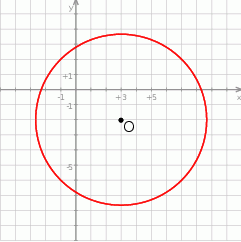
Punkt 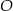 jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
A) 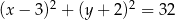 B)
B) 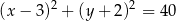
C) 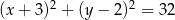 D)
D) 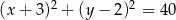
Prosta 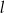 ma równanie
ma równanie 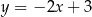 . Równaniem prostej prostopadłej do
. Równaniem prostej prostopadłej do 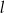 i przechodzącej przez punkt
i przechodzącej przez punkt 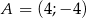 jest:
jest:
A) 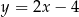 B)
B) 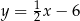 C)
C) 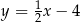 D)
D) 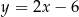
Punkt 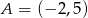 leży na prostej
leży na prostej 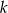 prostopadłej do prostej o równaniu
prostopadłej do prostej o równaniu 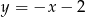 . Prosta
. Prosta 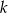 ma równanie
ma równanie
A) 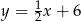 B)
B) 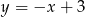 C)
C) 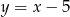 D)
D) 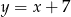
Prosta prostopadła do prostej o równaniu 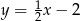 i przechodząca przez punkt
i przechodząca przez punkt 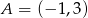 ma równanie
ma równanie
A) 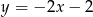 B)
B) 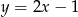 C)
C) 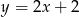 D)
D) 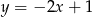
Na płaszczyźnie z układem współrzędnych proste 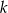 i
i 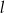 przecinają się pod kątem prostym w punkcie
przecinają się pod kątem prostym w punkcie 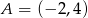 . Prosta
. Prosta 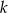 jest określona równaniem
jest określona równaniem 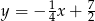 . Zatem prostą
. Zatem prostą 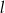 opisuje równanie
opisuje równanie
A) 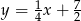 B)
B) 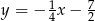 C)
C) 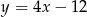 D)
D) 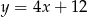
Dana jest prosta 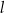 o równaniu
o równaniu 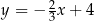 . Prosta
. Prosta 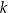 jest prostopadła do prostej
jest prostopadła do prostej 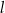 i przechodzi przez punkt
i przechodzi przez punkt 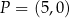 . Prosta
. Prosta 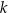 ma równanie
ma równanie
A) 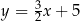 B)
B) 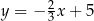 C)
C) 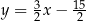 D)
D) 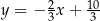
Prosta 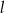 ma równanie
ma równanie 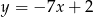 . Równanie prostej prostopadłej do
. Równanie prostej prostopadłej do 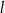 i przechodzącej przez punkt
i przechodzącej przez punkt 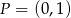 ma postać
ma postać
A) 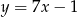 B)
B) 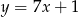 C)
C) 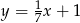 D)
D) 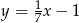
Na płaszczyźnie z układem współrzędnych proste 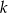 i
i 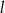 przecinają się pod kątem prostym w punkcie
przecinają się pod kątem prostym w punkcie 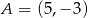 . Prosta
. Prosta 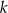 jest określona równaniem
jest określona równaniem 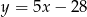 . Zatem prostą
. Zatem prostą 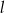 opisuje równanie
opisuje równanie
A) 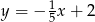 B)
B) 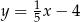 C)
C) 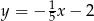 D)
D) 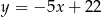
Równanie prostej prostopadłej do prostej 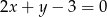 i przechodzącej przez punkt
i przechodzącej przez punkt 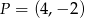 ma postać
ma postać
A) 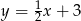 B)
B) 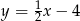 C)
C) 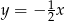 D)
D) 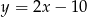
Punkt 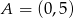 leży na prostej
leży na prostej 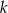 prostopadłej do prostej o równaniu
prostopadłej do prostej o równaniu 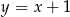 . Prosta
. Prosta 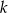 ma równanie
ma równanie
A) 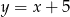 B)
B) 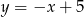 C)
C) 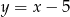 D)
D) 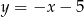
Prosta o równaniu 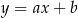 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 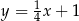 i przechodzi przez punkt
i przechodzi przez punkt 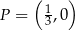 , gdy
, gdy
A) 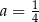 i
i 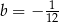 B)
B) 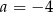 i
i 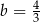
C) 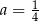 i
i 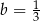 D)
D) 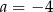 i
i 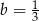
Prostą prostopadłą do prostej 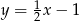 i przechodzącą przez punkt
i przechodzącą przez punkt 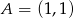 opisuje równanie:
opisuje równanie:
A) 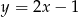 B)
B) 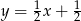 C)
C) 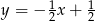 D)
D) 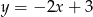
Prosta 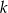 ma równanie
ma równanie 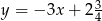 . Wskaż równanie prostej prostopadłej do prostej
. Wskaż równanie prostej prostopadłej do prostej 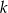 , przechodzącej przez punkt
, przechodzącej przez punkt 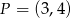 .
.
A) 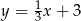 B)
B) 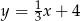 C)
C) 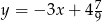 D)
D) 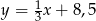
Prosta o równaniu 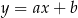 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 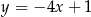 i przechodzi przez punkt
i przechodzi przez punkt 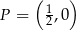 , gdy
, gdy
A) 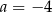 i
i 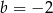 B)
B) 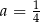 i
i 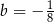
C) 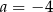 i
i 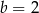 D)
D) 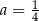 i
i 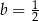
Dana jest prosta 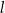 o równaniu
o równaniu 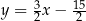 . Prosta
. Prosta 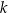 jest prostopadła do prostej
jest prostopadła do prostej 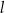 i przechodzi przez punkt
i przechodzi przez punkt 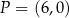 . Prosta
. Prosta 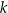 ma równanie
ma równanie
A) 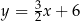 B)
B) 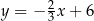 C)
C) 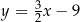 D)
D) 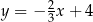
Dana jest prosta 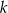 o równaniu
o równaniu 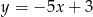 . Równanie prostej prostopadłej do prostej
. Równanie prostej prostopadłej do prostej 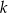 i przechodzącej przez punkt
i przechodzącej przez punkt 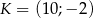 ma postać
ma postać
A) 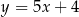 B)
B) 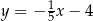 C)
C) 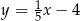 D)
D) 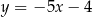
Prosta 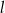 ma równanie
ma równanie 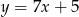 . Równanie prostej prostopadłej do
. Równanie prostej prostopadłej do  i przechodzącej przez punkt
i przechodzącej przez punkt 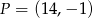 ma postać
ma postać
A) 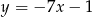 B)
B) 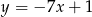 C)
C) 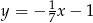 D)
D) 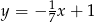
Na okręgu o środku w punkcie  leżą punkty
leżą punkty 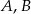 i
i 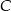 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 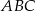 ma miarę
ma miarę 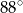 , a kąt
, a kąt 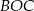 ma miarę o
ma miarę o 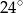 mniejszą od miary kąta
mniejszą od miary kąta 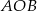 .
.
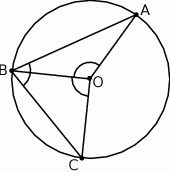
Kąt 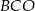 ma miarę
ma miarę
A) 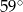 B)
B) 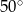 C)
C) 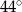 D)
D) 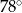
W trójkącie  dane są wierzchołki
dane są wierzchołki 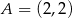 ,
, 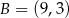 ,
, 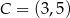 . Trójkąt
. Trójkąt 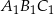 jest obrazem trójkąta
jest obrazem trójkąta 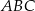 w jednokładności o środku
w jednokładności o środku 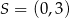 i skali
i skali 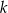 . Trójkąty te leżą po przeciwnych stronach osi rzędnych. Promień okręgu opisanego na trójkącie
. Trójkąty te leżą po przeciwnych stronach osi rzędnych. Promień okręgu opisanego na trójkącie 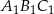 ma długość
ma długość 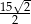 . Skala jednokładności
. Skala jednokładności 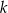 wynosi
wynosi
A) 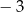 B)
B) 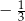 C)
C) 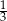 D) 3
D) 3
Ostrosłup ma 12 krawędzi. Liczba wszystkich wierzchołków tego ostrosłupa jest równa
A) 12 B) 9 C) 8 D) 7
Jeśli ostrosłup ma 50 krawędzi, to liczba jego ścian jest równa
A) 50 B) 26 C) 25 D) 22
Ostrosłup, który ma 12 krawędzi, ma
A) 6 ścian B) 7 ścian C) 8 ścian D) 9 ścian
Jeżeli ostrosłup ma 10 krawędzi, to liczba ścian bocznych jest równa
A) 5 B) 7 C) 8 D) 10
Przekątne trapezu  przecinają się w punkcie
przecinają się w punkcie 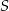 w ten sposób, że
w ten sposób, że 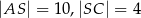 ,
, 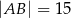 .
.
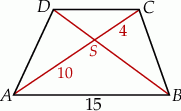
Długość odcinka  jest równa
jest równa
A) 4 B) 6 C) 8 D) 9
Miara kąta ostrego przecięcia prostych przedstawionych na rysunku wynosi
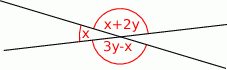
A) 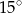 B)
B) 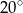 C)
C) 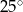 D)
D) 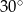
Miara kąta ostrego przecięcia prostych przedstawionych na rysunku wynosi
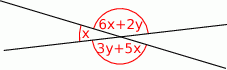
A) 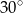 B)
B) 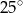 C)
C) 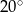 D)
D) 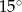
Miara kąta ostrego przecięcia prostych przedstawionych na rysunku wynosi
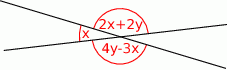
A) 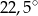 B)
B) 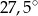 C)
C) 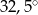 D)
D) 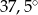
Przyprostokątna 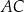 trójkąta prostokątnego
trójkąta prostokątnego 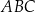 ma długość 8 oraz
ma długość 8 oraz 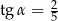 (zobacz rysunek).
(zobacz rysunek).
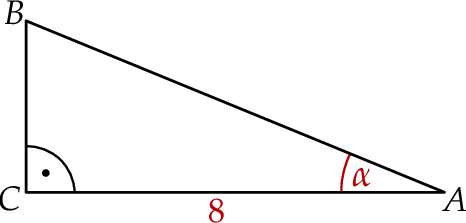
Pole tego trójkąta jest równe
A) 12 B) 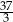 C)
C) 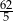 D)
D) 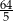
Przyprostokątna 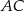 trójkąta prostokątnego
trójkąta prostokątnego 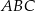 ma długość 14 oraz
ma długość 14 oraz 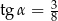 (zobacz rysunek).
(zobacz rysunek).
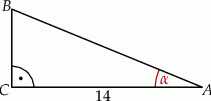
Pole tego trójkąta jest równe
A) 73,5 B) 36,75 C) 5,25 D) 37,3
Prosta o równaniu 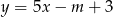 przechodzi przez punkt
przechodzi przez punkt 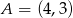 . Wtedy
. Wtedy
A) 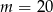 B)
B) 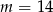 C)
C) 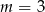 D)
D) 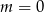
Prosta o równaniu 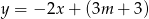 przecina w układzie współrzędnych oś
przecina w układzie współrzędnych oś 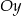 w punkcie
w punkcie 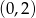 . Wtedy
. Wtedy
A) 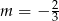 B)
B) 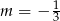 C)
C) 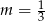 D)
D) 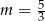
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 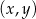 , dana jest prosta
, dana jest prosta 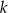 o równaniu
o równaniu 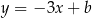 , przechodząca przez punkt
, przechodząca przez punkt 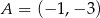 . Współczynnik
. Współczynnik 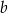 w równaniu tej prostej jest równy
w równaniu tej prostej jest równy
A) 0 B) 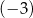 C)
C) 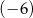 D)
D) 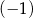
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 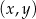 , dana jest prosta
, dana jest prosta  o równaniu
o równaniu 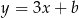 , przechodząca przez punkt
, przechodząca przez punkt 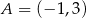 . Współczynnik
. Współczynnik 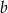 w równaniu tej prostej jest równy
w równaniu tej prostej jest równy
A) 0 B) 6 C) 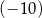 D) 8
D) 8
Punkt o współrzędnych 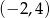 należy do prostej
należy do prostej 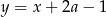 . Zatem
. Zatem
A) 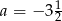 B)
B) 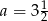 C)
C) 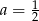 D)
D) 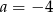
Prosta o równaniu 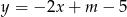 przechodzi przez punkt
przechodzi przez punkt 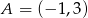 . Wtedy
. Wtedy
A) 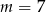 B)
B) 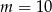 C)
C) 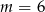 D)
D) 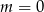
Prosta o równaniu 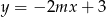 przechodzi przez punkt
przechodzi przez punkt 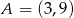 . Wtedy
. Wtedy
A) 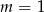 B)
B) 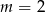 C)
C) 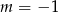 D)
D) 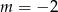
Prosta o równaniu 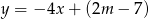 przechodzi przez punkt
przechodzi przez punkt 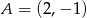 . Wtedy
. Wtedy
A) 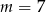 B)
B) 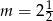 C)
C) 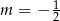 D)
D) 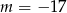
Prosta o równaniu 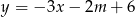 przechodzi przez punkt
przechodzi przez punkt 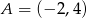 . Wtedy
. Wtedy
A) 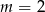 B)
B) 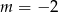 C)
C) 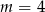 D)
D) 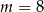
Prosta o równaniu 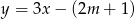 przecina w układzie współrzędnych oś
przecina w układzie współrzędnych oś 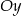 w punkcie
w punkcie 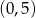 . Wtedy
. Wtedy
A) 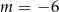 B)
B) 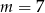 C)
C) 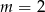 D)
D) 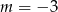
Dany jest sześcian 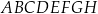 o krawędzi długości 5. Wewnątrz sześcianu znajduje się punkt
o krawędzi długości 5. Wewnątrz sześcianu znajduje się punkt  (zobacz rysunek).
(zobacz rysunek).
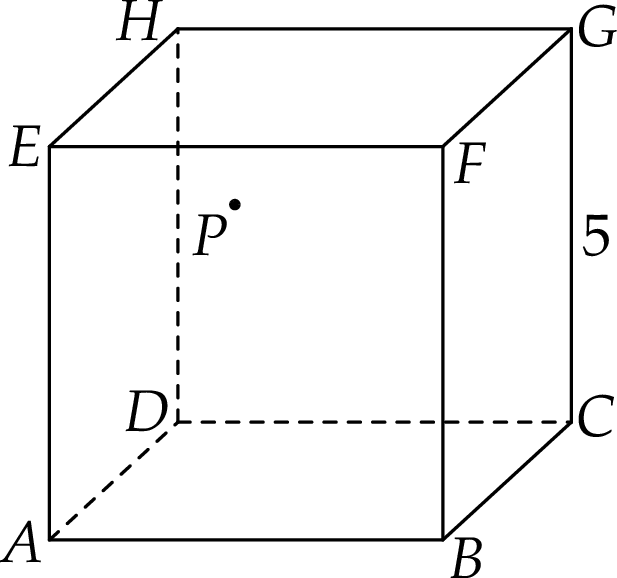
Suma odległości punktu  od wszystkich ścian sześcianu
od wszystkich ścian sześcianu  jest równa
jest równa
A) 15 B) 20 C) 25 D) 30
