Dany jest okrąg o środku w punkcie 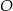 . Prosta
. Prosta 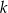 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 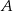 .
.
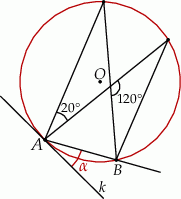
Miara kąta  jest równa
jest równa
A) 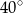 B)
B) 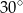 C)
C) 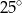 D)
D) 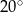
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest okrąg o środku w punkcie 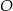 . Prosta
. Prosta 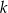 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 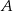 .
.

Miara kąta  jest równa
jest równa
A) 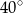 B)
B) 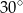 C)
C) 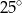 D)
D) 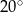
Dany jest okrąg o środku w punkcie 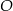 . Prosta
. Prosta 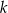 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 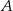 .
.
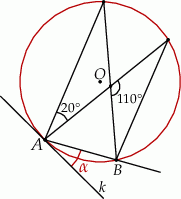
Miara kąta  jest równa
jest równa
A) 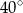 B)
B) 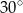 C)
C) 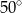 D)
D) 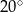
Przeciwległe wierzchołki kwadratu mają współrzędne 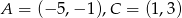 . Promień okręgu wpisanego w ten kwadrat jest równy
. Promień okręgu wpisanego w ten kwadrat jest równy
A) 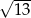 B)
B) 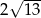 C)
C) 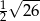 D)
D) 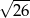
Przeciwległe wierzchołki kwadratu mają współrzędne 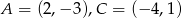 . Średnica okręgu wpisanego w ten kwadrat jest równa
. Średnica okręgu wpisanego w ten kwadrat jest równa
A) 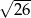 B)
B) 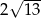 C)
C) 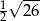 D)
D) 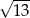
Przeciwległe wierzchołki kwadratu mają współrzędne 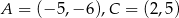 . Promień okręgu wpisanego w ten kwadrat jest równy
. Promień okręgu wpisanego w ten kwadrat jest równy
A) 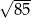 B)
B) 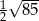 C)
C) 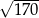 D)
D) 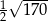
Przeciwległe wierzchołki kwadratu mają współrzędne 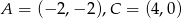 . Promień okręgu wpisanego w ten kwadrat jest równy
. Promień okręgu wpisanego w ten kwadrat jest równy
A) 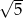 B)
B) 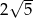 C)
C) 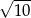 D)
D) 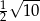
Z prostokąta  o polu 30 wycięto trójkąt
o polu 30 wycięto trójkąt  (tak jak na rysunku). Pole zacieniowanej figury jest równe
(tak jak na rysunku). Pole zacieniowanej figury jest równe
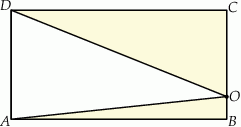
A) 7,5 B) 15 C) 20 D) 25
Z prostokąta  o polu 28 wycięto trójkąt
o polu 28 wycięto trójkąt 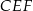 , przy czym punkty
, przy czym punkty 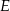 i
i 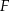 są środkami odpowiednio boków
są środkami odpowiednio boków 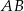 i
i  .
.
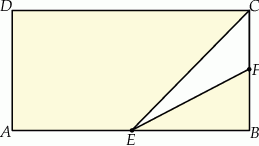
Pole zacieniowanej figury jest równe
A) 3,5 B) 21 C) 25 D) 24,5
Z trójkąta  o obwodzie 50 wycięto kwadrat
o obwodzie 50 wycięto kwadrat  o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
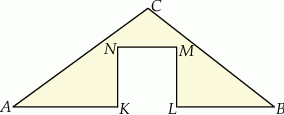
A) 64 B) 60 C) 75 D) 70
W kartezjańskim układzie współrzędnych 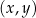 dana jest prosta
dana jest prosta  o równaniu
o równaniu 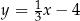 . Prosta o równaniu
. Prosta o równaniu 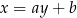 jest równoległa do prostej
jest równoległa do prostej 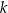 i przechodzi przez punkt
i przechodzi przez punkt 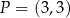 , gdy
, gdy
A) 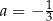 i
i 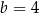 B)
B) 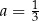 i
i 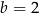 C)
C) 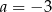 i
i 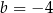 D)
D) 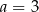 i
i 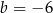
Powierzchnia boczna walca o objętości 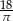 po rozwinięciu jest prostokątem, w którym przekątna tworzy z wysokością walca kąt o mierze
po rozwinięciu jest prostokątem, w którym przekątna tworzy z wysokością walca kąt o mierze 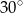 . Promień podstawy tego walca jest równy
. Promień podstawy tego walca jest równy
A) 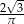 B)
B) 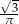 C)
C) 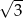 D)
D) 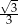
Krawędź podstawy ostrosłupa prawidłowego czworokątnego jest dwa razy dłuższa od jego wysokości. Kąt nachylenia ściany bocznej do podstawy ma miarę
A) 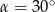 B)
B) 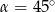 C)
C) 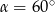 D)
D) 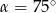
Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma ich miar jest równa 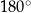 . Jaka jest miara kąta środkowego?
. Jaka jest miara kąta środkowego?
A) 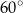 B)
B) 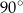 C)
C) 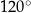 D)
D) 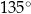
Kąt środkowy i kąt wpisany w okrąg są oparte na tym samym łuku. Suma ich miar jest równa 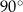 . Miara kata środkowego jest równa
. Miara kata środkowego jest równa
A) 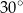 B)
B) 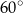 C)
C) 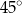 D)
D) 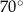
Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma ich miar jest równa 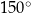 . Jaka jest miara kąta środkowego?
. Jaka jest miara kąta środkowego?
A) 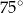 B)
B) 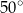 C)
C) 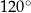 D)
D) 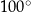
W okręgu 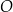 kąt środkowy
kąt środkowy 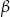 oraz kąt wpisany
oraz kąt wpisany  są oparte na tym samym łuku. Kąt
są oparte na tym samym łuku. Kąt 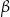 ma miarę o
ma miarę o 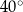 większą od kąta
większą od kąta  . Miara kąta
. Miara kąta 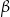 jest równa
jest równa
A) 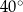 B)
B) 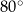 C)
C) 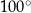 D)
D) 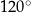
Miara kąta wpisanego w okrąg jest o 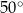 mniejsza od miary kąta środkowego opartego na tym samym łuku. Zatem miara kąta wpisanego jest równa
mniejsza od miary kąta środkowego opartego na tym samym łuku. Zatem miara kąta wpisanego jest równa
A) 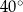 B)
B) 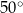 C)
C) 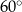 D)
D) 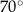
Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma ich miar jest równa 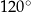 . Jaka jest miara kąta środkowego?
. Jaka jest miara kąta środkowego?
A) 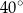 B)
B) 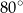 C)
C) 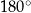 D)
D) 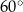
Miara kąta wpisanego w okrąg jest o 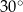 mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa
mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa
A) 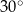 B)
B) 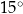 C)
C) 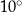 D)
D) 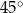
Miara kąta wpisanego w okrąg jest o 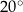 mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa
mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa
A) 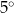 B)
B) 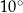 C)
C) 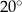 D)
D) 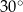
W okręgu 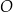 kąt środkowy
kąt środkowy 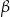 oraz kąt wpisany
oraz kąt wpisany  są oparte na tym samym łuku. Kąt
są oparte na tym samym łuku. Kąt 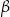 ma miarę o
ma miarę o 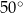 większą od kąta
większą od kąta  . Miara kąta
. Miara kąta 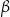 jest równa
jest równa
A) 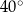 B)
B) 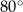 C)
C) 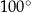 D)
D) 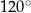
Suma kwadratów długości trzech boków trójkąta prostokątnego jest równa 162. Zatem przeciwprostokątna może mieć długość:
A) 12 B) 81 C) 54 D) 9
Suma kwadratów długości trzech boków trójkąta prostokątnego jest równa 98. Zatem przeciwprostokątna ma długość:
A) 49 B) 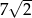 C) 7 D) 9
C) 7 D) 9
Dany jest prostopadłościan  , w którym podstawy
, w którym podstawy 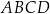 i
i 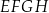 są kwadratami o boku długości 6. Przekątna
są kwadratami o boku długości 6. Przekątna 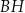 tego prostopadłościanu tworzy z przekątną
tego prostopadłościanu tworzy z przekątną 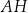 ściany bocznej
ściany bocznej 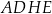 kąt o mierze
kąt o mierze 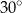 (zobacz rysunek).
(zobacz rysunek).
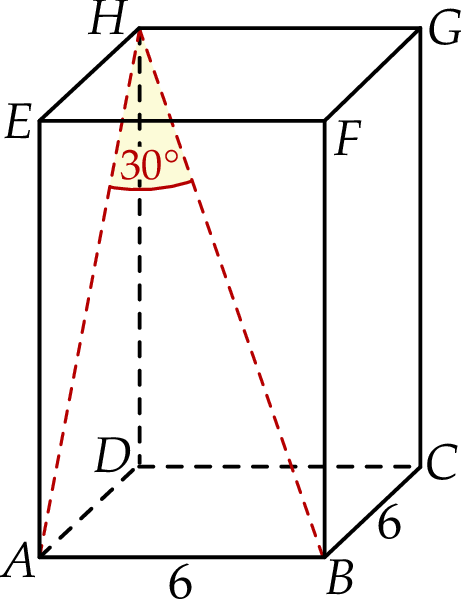
Przekątna 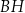 tego prostopadłościanu ma długość równą
tego prostopadłościanu ma długość równą
A) 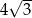 B)
B) 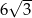 C) 12 D)
C) 12 D) 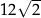
Przekrój osiowy walca jest kwadratem o boku długości 6. Objętość tego walca jest równa
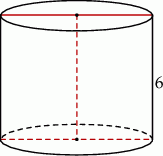
A) 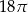 B)
B) 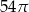 C)
C) 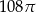 D)
D) 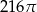
Jeżeli przekrój osiowy walca jest kwadratem o boku 4, to objętość walca jest równa
A) 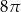 B)
B) 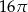 C)
C) 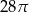 D)
D) 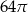
Przekrój osiowy walca jest kwadratem o boku długości 8. Objętość tego walca jest równa
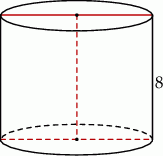
A) 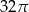 B)
B) 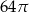 C)
C) 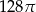 D)
D) 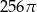
Przekrój osiowy walca jest kwadratem o boku długości 6. Objętość tego walca jest równa
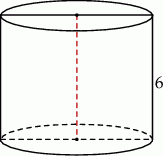
A) 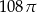 B)
B) 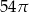 C)
C) 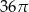 D)
D) 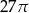
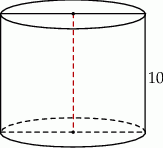
Przekrój osiowy walca jest kwadratem o boku 10. Objętość tego walca jest równa
A) 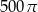 B)
B) 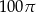 C)
C) 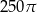 D)
D) 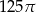
Punkt 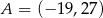 i środek
i środek 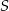 odcinka
odcinka 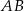 są położone symetrycznie względem początku układu współrzędnych. Zatem punkt
są położone symetrycznie względem początku układu współrzędnych. Zatem punkt 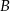 ma współrzędne
ma współrzędne
A) 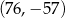 B)
B) 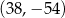 C)
C) 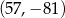 D)
D) 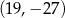
Punkt 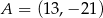 i środek
i środek 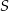 odcinka
odcinka 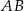 są położone symetrycznie względem początku układu współrzędnych. Zatem punkt
są położone symetrycznie względem początku układu współrzędnych. Zatem punkt 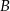 ma współrzędne
ma współrzędne
A) 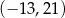 B)
B) 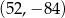 C)
C) 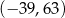 D)
D) 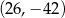
Dane są punkty 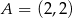 ,
, 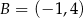 ,
, 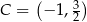 i
i 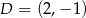 . Pole czworokąta
. Pole czworokąta 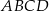 jest równe
jest równe
A) 10,5 B) 16,5 C) 9 D) 8,25
Stosunek pól powierzchni dwóch kul jest równy 1:9. Wobec tego stosunek objętości tych kul jest równy
A) 1:3 B) 1:9 C) 1:27 D) 1:81
Stosunek pól powierzchni dwóch kul jest równy 1:16. Wobec tego stosunek objętości tych kul jest równy
A) 1:256 B) 1:64 C) 1:16 D) 1:4
Stosunek pól powierzchni dwóch kul jest równy 1:4. Wobec tego stosunek objętości tych kul jest równy
A) 1:2 B) 1:8 C) 1:4 D) 1:16
Jeśli promień kuli zwiększymy o 30%, to pole powierzchni kuli wzrośnie o:
A) 30% B) 60% C) 69% D) ponad 100%
Jeśli promień kuli zmniejszymy o 50%, to pole powierzchni kuli zmaleje o:
A) 30% B) 60% C) 75% D) ponad 90%
Jeśli promień kuli zwiększymy o 50%, to pole powierzchni kuli wzrośnie o:
A) 30% B) 60% C) 69% D) ponad 100%
Odległość między środkami stycznych wewnętrznie okręgów o promieniach  i
i 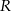 jest równa 7. Odległość między środkami stycznych zewnętrznie okręgów o promieniach
jest równa 7. Odległość między środkami stycznych zewnętrznie okręgów o promieniach  i
i 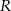 jest równa 23. Promienie
jest równa 23. Promienie  i
i 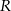 mają długości
mają długości
A) 6 i 17 B) 11 i 12 C) 10 i 13 D) 8 i 15
W trójkącie prostokątnym przeciwprostokątna ma długość 3, a długość przyprostokątnej leżącej naprzeciwko kąta  jest równa
jest równa 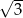 . Zatem
. Zatem
A) 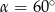 B)
B) 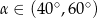 C)
C) 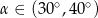 D)
D) 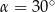
W trójkącie prostokątnym przeciwprostokątna ma długość 3, a długość przyprostokątnej leżącej naprzeciwko kąta  jest równa
jest równa 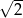 . Zatem
. Zatem
A) 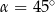 B)
B) 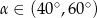 C)
C) 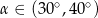 D)
D) 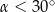
Pole rombu o kącie ostrym 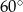 jest równe
jest równe 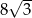 . Bok tego rombu ma długość
. Bok tego rombu ma długość
A) 6 B) 2 C) 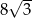 D) 4
D) 4
Pole rombu o kącie ostrym 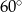 jest równe
jest równe 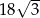 . Bok tego rombu ma długość
. Bok tego rombu ma długość
A) 9 B) 3 C) 6 D) 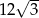
Długości boków trójkąta wychodzących z wierzchołka kąta ostrego  wynoszą odpowiednio 2 dm i 40 cm. Jaką miarę ma kąt
wynoszą odpowiednio 2 dm i 40 cm. Jaką miarę ma kąt  , jeśli pole tego trójkąta jest równe
, jeśli pole tego trójkąta jest równe 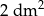 ?
?
A) 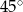 B)
B) 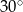 C)
C) 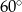 D)
D) 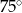
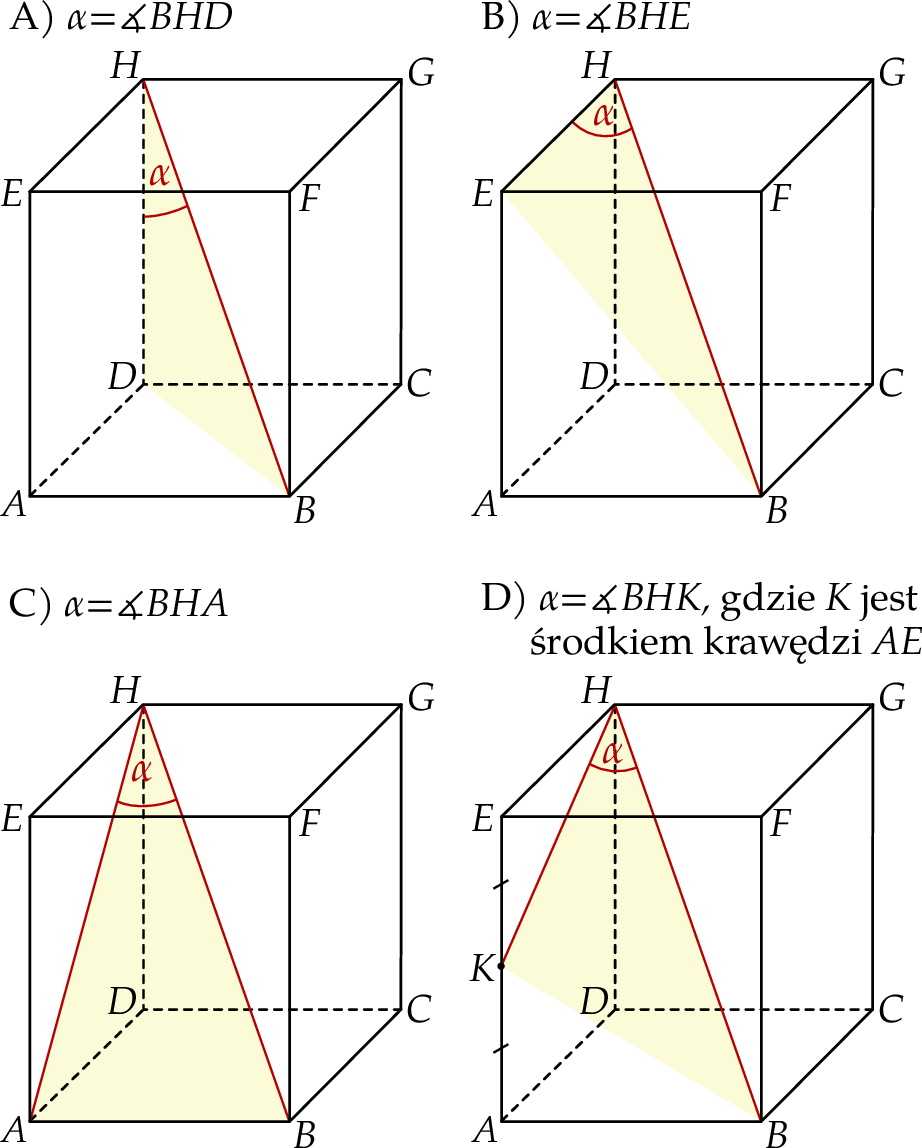
Dany jest prostopadłościan 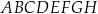 , w którym prostokąty
, w którym prostokąty 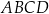 i
i 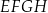 są jego podstawami. Odcinek
są jego podstawami. Odcinek 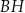 jest przekątną tego prostopadłościanu. Na którym rysunku prawidłowo oznaczono i podpisano kąt
jest przekątną tego prostopadłościanu. Na którym rysunku prawidłowo oznaczono i podpisano kąt  pomiędzy przekątną
pomiędzy przekątną 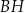 prostopadłościanu a jego ścianą boczną
prostopadłościanu a jego ścianą boczną 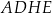 ?
?