Dany jest trójkąt o bokach długości 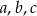 . Stosunek
. Stosunek 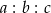 jest równy 3:5:7. Które zdanie jest fałszywe?
jest równy 3:5:7. Które zdanie jest fałszywe?
A) Liczba  jest o 12,5% mniejsza od liczby
jest o 12,5% mniejsza od liczby 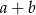
B) Liczba  stanowi 20% liczby
stanowi 20% liczby 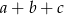
C) Liczba  stanowi 25% liczby
stanowi 25% liczby 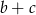
D) Liczba 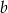 to 60% liczby
to 60% liczby  .
.
/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt/Dowolny
Obwód trójkąta 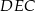 wynosi
wynosi 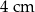 . Wiadomo, że
. Wiadomo, że 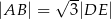 oraz
oraz 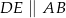 . Zatem obwód trójkąta
. Zatem obwód trójkąta 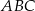 jest równy
jest równy
A) 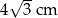 B)
B) 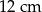 C)
C) 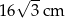 D)
D) 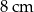
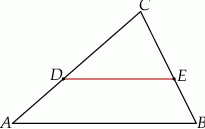
Obwód trójkąta 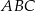 jest równy 40 cm. Punkt
jest równy 40 cm. Punkt 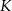 leży na boku
leży na boku 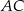 , a punkt
, a punkt 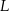 na boku
na boku 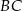 tak, że odcinek
tak, że odcinek 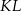 jest równoległy do boku
jest równoległy do boku 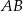 trójkąta i
trójkąta i 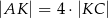 . Obwód trójkąta
. Obwód trójkąta 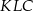 jest równy:
jest równy:
A) 10 cm B) 4 cm C) 8 cm D) 5 cm
Pole trójkąta, w którym wysokość jest o 3 cm dłuższa od podstawy jest równe 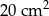 Wysokość trójkąta jest równa:
Wysokość trójkąta jest równa:
A) 5 cm B) 8 cm C) 2 cm D) 11 cm
Jeżeli środek okręgu opisanego na trójkącie leży na wysokości trójkąta, to trójkąt ten musi być
A) równoboczny B) równoramienny C) prostokątny D) rozwartokątny
Jeżeli środek okręgu wpisanego w trójkąt leży na wysokości trójkąta, to trójkąt ten musi być
A) rozwartokątny B) prostokątny C) równoramienny D) równoboczny
Odcinki 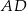 i
i 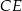 są wysokościami trójkąta
są wysokościami trójkąta 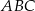 .
.
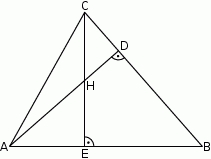
Zatem
A) 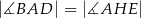 B)
B) 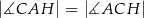
C) 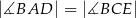 D)
D) 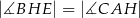
W trójkącie stosunek miar kątów jest równy 3:4:5. Zatem najmniejszy kąt tego trójkąta ma miarę
A) 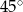 B)
B) 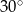 C)
C) 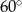 D)
D) 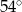
Miary kątów wewnętrznych pewnego trójkąta pozostają w stosunku 2:4:9. Największy kąt wewnętrzny tego trójkąta ma miarę
A) 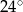 B)
B) 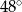 C)
C) 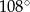 D)
D) 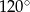
Miary kątów wewnętrznych pewnego trójkąta pozostają w stosunku 3:4:5. Najmniejszy kąt wewnętrzny tego trójkąta ma miarę
A) 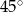 B)
B) 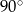 C)
C) 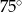 D)
D) 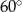
Dwa trójkąty podobne mają pola równe odpowiednio 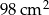 ,
, 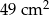 . Skala podobieństwa jest równa
. Skala podobieństwa jest równa
A) 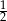 B) 2 C) 4 D)
B) 2 C) 4 D) 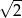
Jeżeli trójkąty 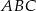 i
i 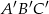 są podobne, a ich pola są, odpowiednio, równe
są podobne, a ich pola są, odpowiednio, równe 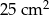 i
i 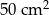 , to skala podobieństwa
, to skala podobieństwa 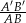 jest równa
jest równa
A) 2 B) 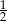 C)
C) 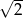 D)
D) 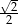
Dwa trójkąty podobne mają pola równe odpowiednio 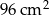 ,
, 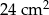 . Skala podobieństwa jest równa
. Skala podobieństwa jest równa
A) 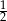 B) 4 C) 2 D)
B) 4 C) 2 D) 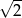
Dwa trójkąty podobne mają pola równe odpowiednio 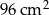 ,
, 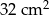 . Skala podobieństwa jest równa
. Skala podobieństwa jest równa
A) 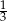 B)
B) 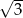 C) 9 D) 3
C) 9 D) 3
Trójkąt 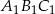 o polu
o polu 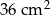 jest podobny do trójkąta
jest podobny do trójkąta 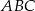 o polu
o polu 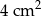 . Skala podobieństwa trójkąta
. Skala podobieństwa trójkąta 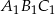 do trójkąta
do trójkąta 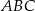 jest równa
jest równa
A) 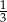 B) 9 C) 12 D) 3
B) 9 C) 12 D) 3
Na rysunkach I, II i III dane są trzy trójkąty.
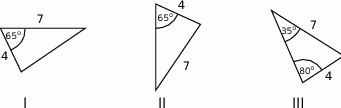
Przystające są trójkąty tylko na rysunkach
A) I i II B) I i III C) II i III D) I, II i III
Na rysunkach I, II i III dane są trzy trójkąty.
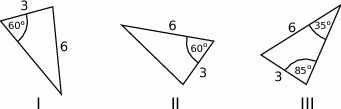
Przystające są trójkąty tylko na rysunkach
A) I i II B) I i III C) II i III D) I, II i III
Na rysunkach I, II i III dane są trzy trójkąty.
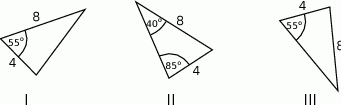
Na których rysunkach trójkąty są przystające?
A) I i II B) I i III C) II i III D) I, II i III
W trójkącie 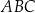 bok
bok 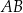 ma długość
ma długość 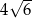 . Ponadto
. Ponadto 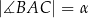 ,
, 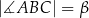 oraz
oraz 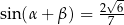 . Długość okręgu opisanego na trójkącie
. Długość okręgu opisanego na trójkącie 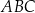 jest równa
jest równa
A) 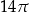 B)
B) 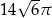 C)
C) 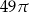 D)
D) 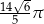
W trójkącie 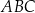 długość boku
długość boku 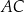 jest równa 3, a długość boku
jest równa 3, a długość boku 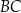 jest równa 4. Dwusieczna kąta
jest równa 4. Dwusieczna kąta 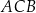 przecina bok
przecina bok 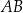 w punkcie
w punkcie 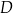 . Stosunek
. Stosunek 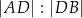 jest równy
jest równy
A) 4 : 3 B) 4 : 7 C) 3 : 4 D) 3 : 7
W trójkącie 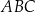 długość boku
długość boku 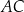 jest równa 6, a długość boku
jest równa 6, a długość boku 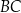 jest równa 8. Dwusieczna kąta
jest równa 8. Dwusieczna kąta 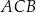 przecina bok
przecina bok 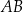 w punkcie
w punkcie 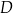 . Stosunek
. Stosunek 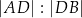 jest równy
jest równy
A) 4 : 3 B) 3 : 4 C) 4 : 7 D) 3 : 7
W trójkącie 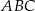 punkt
punkt 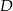 leży na boku
leży na boku 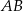 , punkt
, punkt 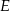 leży na boku
leży na boku 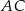 , a ponadto odcinek
, a ponadto odcinek 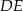 jest równoległy do boku
jest równoległy do boku 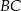 i
i 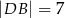 . Pole trójkąta
. Pole trójkąta 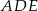 jest równe 12, a pole trapezu
jest równe 12, a pole trapezu 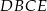 jest równe 15 (zobacz rysunek).
jest równe 15 (zobacz rysunek).
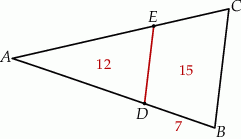
Odcinek 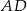 ma długość
ma długość
A) 5,6 B) 12 C) 14 D) 9
Trójkąt, w którym stosunek długości boków jest równy 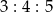 , jest
, jest
A) równoboczny B) prostokątny C) ostrokątny D) rozwartokątny
Boki trójkąta mają długości 20 i 12, a kąt między tymi bokami ma miarę 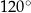 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 60 B) 120 C) 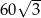 D)
D) 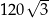
Pole trójkąta o bokach długości 8 oraz 15 i kącie między nimi o mierze 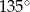 jest równe
jest równe
A) 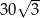 B)
B) 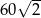 C)
C) 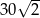 D)
D) 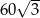
Boki trójkąta mają długości 30 i 8, a kąt między tymi bokami ma miarę 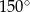 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 60 B) 120 C) 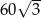 D)
D) 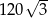
Naprzeciwko boków 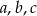 trójkąta
trójkąta 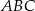 znajdują się odpowiednio kąty
znajdują się odpowiednio kąty 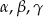 . Wiadomo, że
. Wiadomo, że 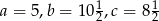 . Wówczas
. Wówczas
A) 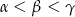 B)
B) 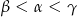 C)
C) 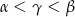 D)
D) 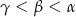
Naprzeciwko boków 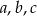 trójkąta
trójkąta 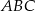 znajdują się odpowiednio kąty
znajdują się odpowiednio kąty 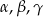 . Wiadomo, że
. Wiadomo, że 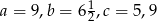 . Wówczas
. Wówczas
A) 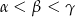 B)
B) 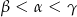 C)
C) 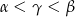 D)
D) 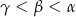
Naprzeciwko boków 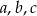 trójkąta
trójkąta 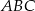 znajdują się odpowiednio kąty
znajdują się odpowiednio kąty 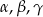 . Wiadomo, że
. Wiadomo, że 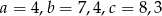 . Wówczas
. Wówczas
A) 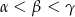 B)
B) 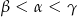 C)
C) 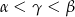 D)
D) 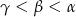
Miary kątów trójkąta pozostają w stosunku 4:5:6. Miary kątów tego trójkąta są równe
A) 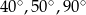 B)
B) 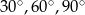 C)
C) 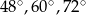 D)
D) 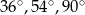
Trójkąt można zbudować z odcinków o długościach:
A) 10, 6, 5 B) 4, 2, 1 C) 8, 5, 3 D) 6, 6, 13
Trójkąt można zbudować z odcinków o długościach:
A) 4, 2, 2 B) 7, 4, 3 C) 5, 6, 12 D) 8, 4, 5
Długościami boków trójkąta mogą być odcinki:
A) 5 cm, 8 cm, 2 cm B) 9 cm, 4 cm, 4 cm C) 3 cm, 2 cm, 1 cm D) 7 cm, 9 cm, 10 cm
Można zbudować trójkąt z odcinków 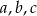 jeśli
jeśli
A) 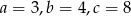
B) 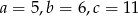
C) 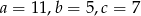
D) 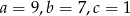
Jeśli 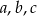 są długościami odcinków, to istnieje trójkąt o bokach
są długościami odcinków, to istnieje trójkąt o bokach 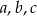 , jeżeli
, jeżeli
A) 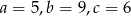
B) 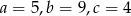
C) 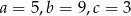
D) 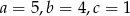
Na rysunku przedstawiono okrąg o środku 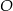 , który jest wpisany w trójkąt
, który jest wpisany w trójkąt 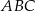 .
.
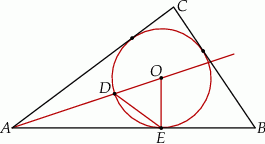
Okrąg ten przecina bok 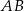 w punkcie
w punkcie 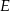 , a odcinek
, a odcinek 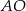 w punkcie
w punkcie 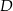 . Jeżeli
. Jeżeli 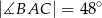 , to miara kąta
, to miara kąta 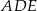 jest równa
jest równa
A) 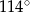 B)
B) 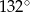 C)
C) 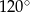 D)
D) 
W trójkącie 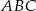 na rysunku obok dane są:
na rysunku obok dane są: 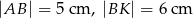 oraz
oraz 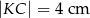 . Wiadomo, że
. Wiadomo, że 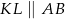 .
.
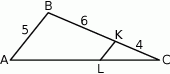
Wówczas:
A) 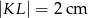 B)
B) 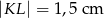 C)
C) 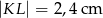 D)
D) 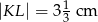
W trójkącie 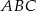 punkt
punkt 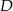 leży na boku
leży na boku 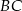 , a punkt
, a punkt 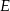 leży na boku
leży na boku 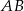 . Odcinek
. Odcinek 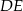 jest równoległy do boku
jest równoległy do boku 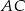 , a ponadto
, a ponadto  ,
, 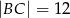 i
i 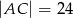 (zobacz rysunek).
(zobacz rysunek).
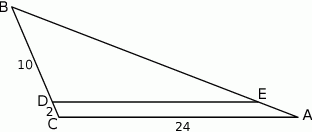
Długość odcinka 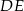 jest równa
jest równa
A) 22 B) 20 C) 12 D) 11
W trójkącie 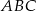 punkt
punkt 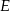 leży na boku
leży na boku 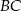 , a punkt
, a punkt 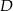 leży na boku
leży na boku 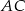 . Odcinek
. Odcinek 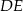 jest równoległy do boku
jest równoległy do boku 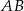 , a ponadto
, a ponadto 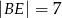 ,
, 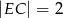 i
i 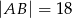 (zobacz rysunek).
(zobacz rysunek).
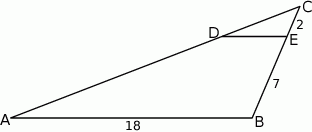
Długość odcinka 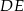 jest równa
jest równa
A) 5 B) 3 C) 6 D) 4
Dany jest trójkąt, którego kąty mają miary 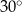 ,
, 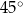 oraz
oraz 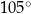 . Długości boków trójkąta, leżących naprzeciwko tych kątów są równe – odpowiednio –
. Długości boków trójkąta, leżących naprzeciwko tych kątów są równe – odpowiednio –  ,
, 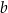 oraz
oraz  (zobacz rysunek).
(zobacz rysunek).

Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A–F. Pole tego trójkąta poprawnie określa wyrażenie
A) 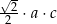 B)
B) 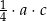 C)
C) 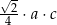
D) 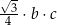 E)
E) 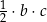 F)
F) 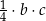
Dany jest trójkąt, którego kąty mają miary 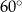 ,
, 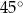 oraz
oraz 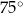 . Długości boków trójkąta, leżących naprzeciwko tych kątów są równe – odpowiednio –
. Długości boków trójkąta, leżących naprzeciwko tych kątów są równe – odpowiednio –  ,
, 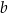 oraz
oraz  (zobacz rysunek).
(zobacz rysunek).
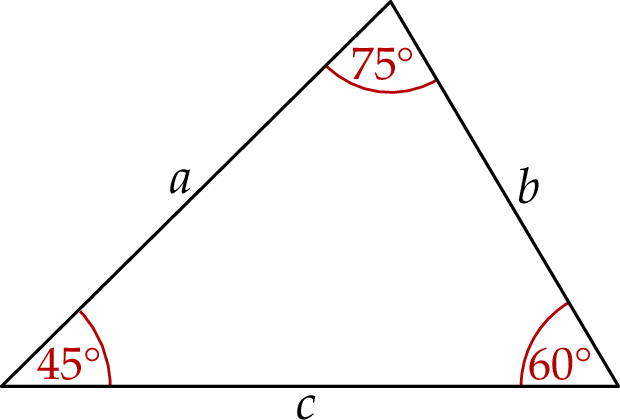
Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A–F. Pole tego trójkąta poprawnie określa wyrażenie
A) 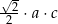 B)
B) 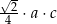 C)
C) 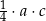
D) 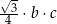 E)
E) 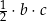 F)
F) 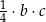
Długości boków trójkąta są liczbami całkowitymi. Jeden bok ma 7 cm, a drugi ma 2 cm. Trzeci bok tego trójkąta może mieć długość
A) 12 cm B) 9 cm C) 6 cm D) 3 cm
Długości boków trójkąta są liczbami całkowitymi. Jeden bok ma 4 cm, a drugi ma 9 cm. Trzeci bok tego trójkąta może mieć długość
A) 4 cm B) 5 cm C) 14 cm D) 9 cm

