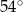Znajdź skalę podobieństwa trójkąta 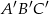 do trójkąta
do trójkąta 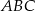 :
:
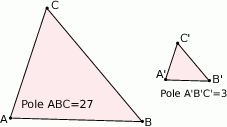
A) 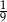 B)
B) 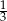 C) 3 D) 9
C) 3 D) 9
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Znajdź skalę podobieństwa trójkąta 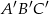 do trójkąta
do trójkąta 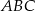 :
:

A) 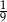 B)
B) 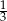 C) 3 D) 9
C) 3 D) 9
Znajdź skalę podobieństwa trójkąta 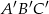 do trójkąta
do trójkąta 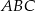 :
:
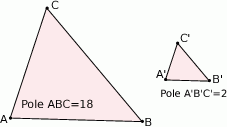
A) 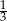 B)
B) 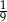 C) 3 D) 9
C) 3 D) 9
W trójkącie 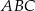 bok
bok 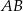 ma długość 4, a bok
ma długość 4, a bok 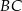 ma długość 4,6. Dwusieczna kąta
ma długość 4,6. Dwusieczna kąta 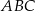 przecina bok
przecina bok 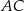 w punkcie
w punkcie 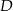 takim, że
takim, że 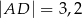 (zobacz rysunek).
(zobacz rysunek).
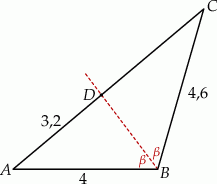
Odcinek 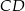 ma długość
ma długość
A) 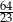 B)
B) 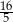 C)
C) 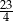 D)
D) 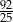
Odcinki 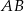 i
i 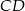 są równoległe. Długości odcinków
są równoległe. Długości odcinków 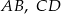 i
i 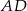 są podane na rysunku.
są podane na rysunku.
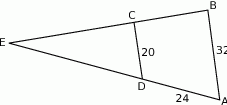
Długość odcinka 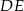 jest równa
jest równa
A) 44 B) 40 C) 36 D) 15
Odcinki 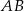 i
i 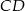 są równoległe i
są równoległe i 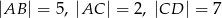 (zobacz rysunek). Długość odcinka
(zobacz rysunek). Długość odcinka 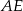 jest równa
jest równa
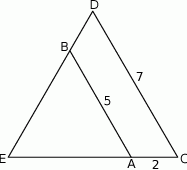
A) 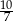 B)
B) 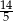 C) 3 D) 5
C) 3 D) 5
Odcinki 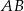 i
i 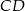 są równoległe. Długości odcinków
są równoległe. Długości odcinków 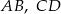 i
i  są podane na rysunku.
są podane na rysunku.
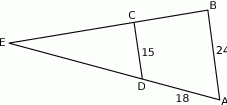
Długość odcinka 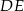 jest równa
jest równa
A) 30 B) 33 C) 27 D) 12
Odcinki 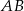 i
i 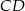 są równoległe i
są równoległe i 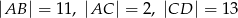 (zobacz rysunek). Długość odcinka
(zobacz rysunek). Długość odcinka 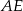 jest równa
jest równa
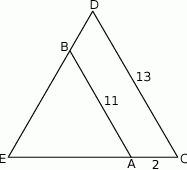
A) 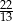 B)
B) 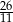 C) 11 D) 13
C) 11 D) 13
Dany jest trójkąt 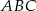 o kącie
o kącie 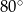 przy wierzchołku
przy wierzchołku 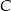 . Kąt między dwusieczną tego kąta a wysokością poprowadzoną z wierzchołka
. Kąt między dwusieczną tego kąta a wysokością poprowadzoną z wierzchołka 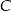 ma miarę
ma miarę 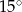 . Wynika stąd, że kąt
. Wynika stąd, że kąt 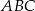 jest równy
jest równy
A) 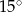 B)
B) 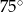 C)
C) 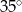 D)
D) 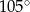
Dany jest trójkąt 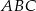 o kącie
o kącie 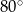 przy wierzchołku
przy wierzchołku 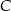 . Kąt między dwusieczną tego kąta a wysokością poprowadzoną z wierzchołka
. Kąt między dwusieczną tego kąta a wysokością poprowadzoną z wierzchołka 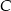 ma miarę
ma miarę 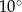 . Wynika stąd, że kąt
. Wynika stąd, że kąt 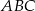 jest równy
jest równy
A) 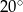 B)
B) 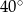 C)
C) 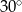 D)
D) 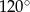
Dany jest trójkąt 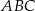 o bokach
o bokach 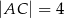 ,
, 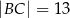 ,
, 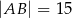 . Sinus kąta
. Sinus kąta 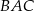 jest równy
jest równy  , a dwusieczne kątów
, a dwusieczne kątów 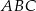 i
i 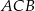 przecinają się w punkcie
przecinają się w punkcie 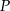 (zobacz rysunek).
(zobacz rysunek).
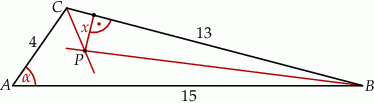
Odległość  punktu
punktu 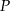 od prostej
od prostej 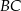 jest równa
jest równa
A) 2 B) 1 C)  D)
D) 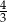
W trójkącie 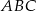 długość środkowej
długość środkowej 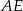 jest równa połowie długości boku
jest równa połowie długości boku 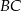 . Wówczas trójkąt
. Wówczas trójkąt 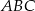 jest trójkątem
jest trójkątem
A) ostrokątnym B) prostokątnym C) rozwartokątnym D) równobocznym
W trójkącie 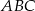 poprowadzono środkową
poprowadzono środkową 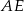 i okazało się, że
i okazało się, że 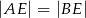 . Zatem trójkąt
. Zatem trójkąt 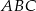 jest trójkątem
jest trójkątem
A) ostrokątnym B) równobocznym C) równoramiennym D) prostokątnym
Pole trójkąta ostrokątnego o bokach 5 i 6 jest równe 9. Długość trzeciego boku tego trójkąta jest równa
A) 5 B) 6 C) 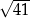 D)
D) 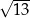
Dany jest trójkąt 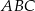 , w którym
, w którym 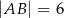 ,
, 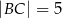 ,
, 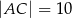 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Cosinus kąta 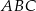 jest równy jest równy 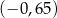 . . | P | F |
Trójkąt 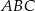 jest rozwartokątny. jest rozwartokątny. | P | F |
Dany jest trójkąt 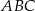 , w którym
, w którym 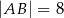 ,
, 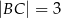 ,
, 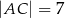 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Cosinus kąta 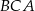 jest równy jest równy 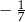 . . | P | F |
Trójkąt 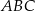 jest ostrokątny. jest ostrokątny. | P | F |
Wierzchołki trójkąta 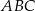 leżą na okręgu i środek
leżą na okręgu i środek 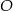 okręgu leży wewnątrz trójkąta. Jeśli kąt
okręgu leży wewnątrz trójkąta. Jeśli kąt 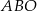 ma miarę
ma miarę 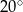 , to kąt
, to kąt 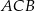 ma miarę
ma miarę
A) 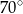 B)
B) 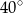 C)
C) 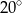 D)
D) 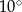
Wierzchołki trójkąta 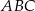 leżą na okręgu i środek
leżą na okręgu i środek 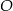 okręgu leży wewnątrz trójkąta. Jeśli kąt
okręgu leży wewnątrz trójkąta. Jeśli kąt 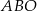 ma miarę
ma miarę 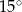 , to kąt
, to kąt 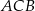 ma miarę
ma miarę
A) 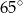 B)
B) 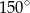 C)
C) 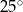 D)
D) 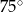
Na trójkącie ostrokątnym 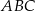 opisano okrąg o środku
opisano okrąg o środku 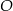 . Miara kąta
. Miara kąta 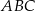 jest równa
jest równa 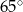 . Miara kąta
. Miara kąta 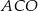 jest równa
jest równa
A) 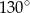 B)
B) 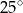 C)
C) 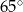 D)
D) 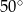
Wierzchołki trójkąta 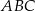 leżą na okręgu i środek
leżą na okręgu i środek 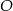 okręgu leży wewnątrz trójkąta. Jeśli kąt
okręgu leży wewnątrz trójkąta. Jeśli kąt 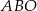 ma miarę
ma miarę 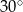 , to kąt
, to kąt 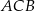 ma miarę
ma miarę
A) 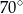 B)
B) 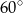 C)
C) 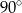 D)
D) 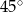
Dwa krótsze boki trójkąta rozwartokątnego 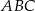 mają długości
mają długości 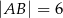 i
i 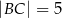 . Sinus największego kąta tego trójkąta jest równy
. Sinus największego kąta tego trójkąta jest równy  . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 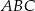 jest mniejsze od 10. jest mniejsze od 10. | P | F |
Cosinus kąta 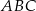 trójkąta trójkąta 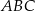 jest równy jest równy 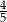 . . | P | F |
Punkt 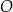 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 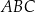 oraz
oraz 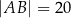 ,
, 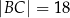 . Prosta
. Prosta 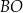 przecina bok
przecina bok 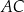 trójkąta
trójkąta 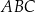 w punkcie
w punkcie 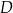 (zobacz rysunek).
(zobacz rysunek).

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Proste 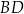 i i 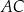 są prostopadłe. są prostopadłe. | P | F |
Stosunek pól trójkątów 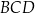 i i 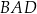 jest równy 0,9. jest równy 0,9. | P | F |
W trójkącie 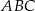 bok
bok 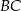 ma długość 13, a wysokość
ma długość 13, a wysokość 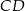 tego trójkąta dzieli bok
tego trójkąta dzieli bok 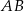 na odcinki o długościach
na odcinki o długościach 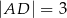 i
i 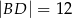 (zobacz rysunek obok).
(zobacz rysunek obok).
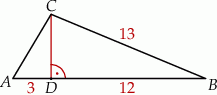
Długość boku 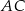 jest równa
jest równa
A) 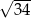 B)
B) 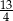 C)
C) 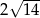 D)
D) 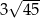
W trójkącie 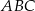 bok
bok 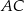 ma długość 10, a wysokość
ma długość 10, a wysokość 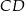 tego trójkąta dzieli bok
tego trójkąta dzieli bok 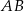 na odcinki o długościach
na odcinki o długościach 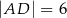 i
i 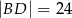 (zobacz rysunek obok).
(zobacz rysunek obok).
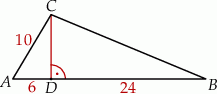
Długość boku 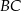 jest równa
jest równa
A) 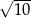 B)
B) 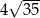 C)
C) 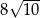 D)
D) 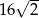
W trójkącie równoramiennym 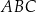 długość podstawy
długość podstawy 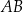 jest równa 4, a długość ramienia
jest równa 4, a długość ramienia 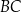 jest równa 6. Dwusieczna kąta
jest równa 6. Dwusieczna kąta 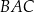 przecina bok
przecina bok 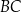 w punkcie
w punkcie 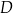 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 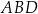 jest prostokątny. jest prostokątny. | P | F |
Odcinek 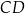 jest krótszy od odcinka jest krótszy od odcinka 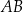 . . | P | F |
Pole trójkąta przedstawionego na rysunku jest równe
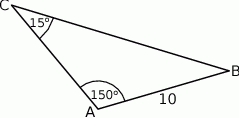
A) 50 B) 25 C) 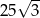 D)
D) 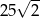
Pole trójkąta o bokach 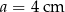 i
i 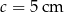 oraz kącie
oraz kącie 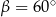 zawartym między danymi bokami jest równe
zawartym między danymi bokami jest równe
A) 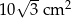 B)
B) 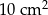 C)
C) 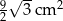 D)
D) 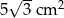
Ile wynosi pole trójkąta, w którym dwa boki mają długości 7 i 12, a kąt zawarty między nimi wynosi 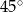 ?
?
A) 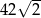 B) 42 C)
B) 42 C) 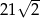 D) 21
D) 21
Pole trójkąta o bokach długości 4 oraz 9 i kącie między nimi o mierze 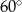 jest równe
jest równe
A) 18 B) 9 C) 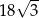 D)
D) 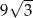
Pole trójkąta o bokach 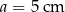 i
i 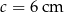 oraz kącie
oraz kącie 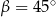 zawartym między danymi bokami jest równe
zawartym między danymi bokami jest równe
A) 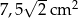 B)
B) 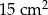 C)
C) 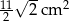 D)
D) 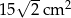
Dany jest trójkąt 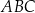 , w którym
, w którym 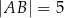 ,
, 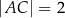 oraz
oraz 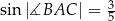 . Pole trójkąta
. Pole trójkąta 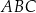 jest równe
jest równe
A) 3 B) 5 C) 6 D) 10
Długości boków trójkąta wynoszą 2 i 8, zaś kąt między nimi zawarty ma miarę 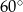 . Pole tego trójkąta wynosi
. Pole tego trójkąta wynosi
A) 8 B) 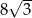 C) 4 D)
C) 4 D) 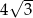
Liczby naturalne 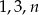 są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
A) 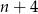 B)
B) 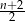 C)
C)  D) 3
D) 3
Liczby naturalne 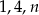 są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
A) 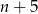 B)
B) 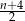 C) 4 D)
C) 4 D) 
Punkty 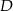 i
i 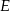 dzielą bok
dzielą bok 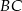 trójkąta
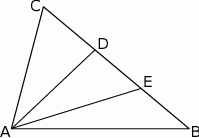
trójkąta 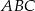 na trzy odcinki, których stosunek długości
na trzy odcinki, których stosunek długości 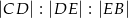 jest równy 8:9:10 (zobacz rysunek). Stosunek pól trójkątów
jest równy 8:9:10 (zobacz rysunek). Stosunek pól trójkątów 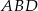 i
i 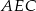 jest równy
jest równy
A)  B)
B) 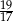 C)
C) 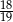 D)
D) 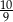
Jeśli jeden bok trójkąta ma długość 3 a drugi 5, to długość trzeciego boku nie może być równa
A) 9 B) 7 C) 6 D) 5
Długości boków trójkąta nie mogą być równe:
A) 3, 4, 4 B) 3, 4, 5 C) 3, 4, 2 D) 3, 4, 8
Wierzchołki trójkąta 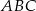 leżą na okręgu o środku
leżą na okręgu o środku 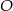 .
. 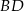 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 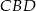 ma miarę
ma miarę 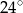 , to kąt
, to kąt 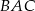 ma miarę
ma miarę
A) 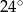 B)
B) 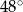 C)
C) 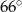 D)
D) 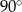
Wierzchołki trójkąta 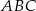 leżą na okręgu o środku
leżą na okręgu o środku 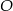 .
. 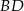 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 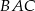 ma miarę
ma miarę 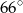 , to kąt
, to kąt 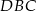 ma miarę
ma miarę
A) 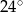 B)
B) 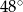 C)
C) 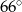 D)
D) 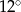
Wierzchołki trójkąta 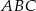 leżą na okręgu o środku
leżą na okręgu o środku 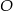 .
. 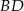 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 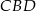 ma miarę
ma miarę 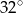 , to kąt
, to kąt 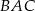 ma miarę
ma miarę
A) 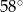 B)
B) 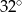 C)
C) 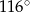 D)
D) 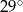
Punkty 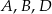 leżą na jednej prostej. Odcinek
leżą na jednej prostej. Odcinek 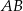 jest podstawą trójkąta równoramiennego
jest podstawą trójkąta równoramiennego  (zobacz rysunek).
(zobacz rysunek).
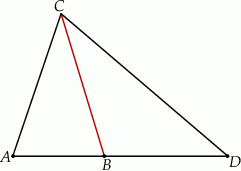
Jeżeli 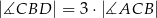 , to
, to 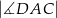 wynosi
wynosi
A) 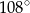 B)
B) 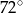 C)
C) 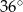 D)
D)