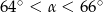Obwód trójkąta 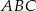 wynosi 24 cm. Połączono środki boków tego trójkąta i otrzymano trójkąt
wynosi 24 cm. Połączono środki boków tego trójkąta i otrzymano trójkąt 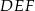 , którego obwód jest równy
, którego obwód jest równy
A) 6 cm B) 8 cm C) 12 cm D) 18 cm
/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt/Dowolny
Na bokach 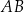 i
i 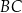 trójkąta
trójkąta 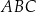 wybrano odpowiednio punkty
wybrano odpowiednio punkty 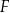 i
i 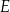 w ten sposób, że
w ten sposób, że 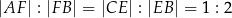 . Odcinki
. Odcinki 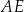 i
i 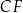 przecinają się w punkcie
przecinają się w punkcie 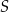 (zobacz rysunek).
(zobacz rysunek).
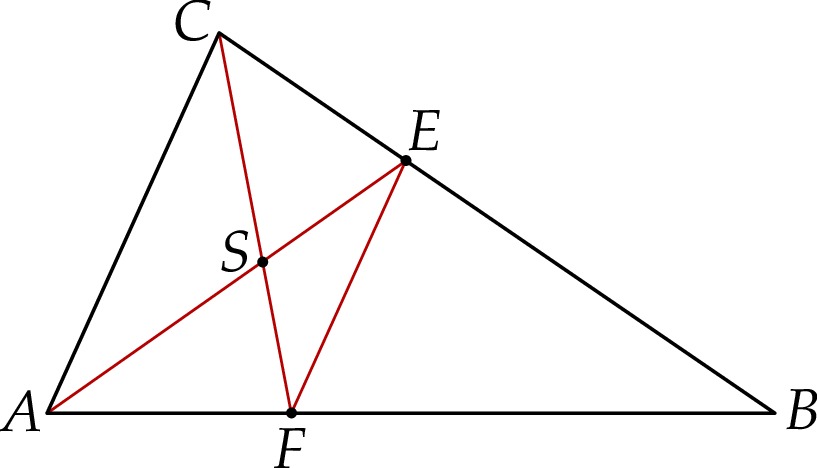
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 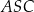 jest podobny do trójkąta jest podobny do trójkąta 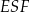 . . | P | F |
Pole trójkąta 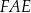 jest równe polu trójkąta jest równe polu trójkąta 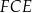 . . | P | F |
Liczby 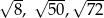 są długościami trójkąta
są długościami trójkąta 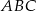 . Trójkątem podobnym do trójkąta
. Trójkątem podobnym do trójkąta 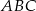 jest trójkąt o bokach długości
jest trójkąt o bokach długości
A) 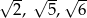 B) 4, 25, 36 C) 8, 50, 72 D) 2, 5, 6
B) 4, 25, 36 C) 8, 50, 72 D) 2, 5, 6
Dany jest trójkąt o bokach długości 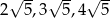 . Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
. Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
A) 10, 15, 20 B) 20, 45, 80 C) 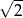 ,
, 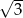 ,
, 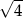 D)
D) 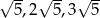
Liczby 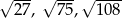 są długościami trójkąta
są długościami trójkąta 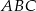 . Trójkątem podobnym do trójkąta
. Trójkątem podobnym do trójkąta 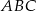 jest trójkąt o bokach długości
jest trójkąt o bokach długości
A) 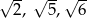 B) 6, 10, 12 C) 8, 50, 72 D) 2, 5, 6
B) 6, 10, 12 C) 8, 50, 72 D) 2, 5, 6
Do trójkąta o bokach długości 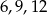 jest podobny trójkąt o bokach
jest podobny trójkąt o bokach
A) 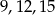 B)
B) 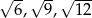 C)
C) 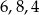 D)
D) 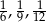
Dany jest trójkąt o bokach długości 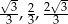 . Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
. Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
A) 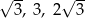 B)
B) 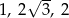 C)
C) 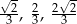 D)
D) 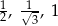
Boki trójkąta 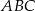 mają długości
mają długości 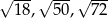 . Trójkątem do niego podobnym jest trójkąt o bokach
. Trójkątem do niego podobnym jest trójkąt o bokach
A) 3, 5, 6 B) 9, 25, 36 C) 18, 50, 72 D) 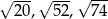
Środkiem okręgu opisanego na trójkącie jest punkt przecięcia się
A) dwusiecznych kątów trójkąta B) środkowych trójkąta
C) wysokości trójkąta D) symetralnych boków trójkąta
Dla dowolnego trójkąta prawdziwe jest zdanie
A) Środek okręgu wpisanego w trójkąt to punkt przecięcia się środkowych trójkąta.
B) Środek okręgu wpisanego w trójkąt to punkt przecięcia się dwusiecznych kątów trójkąta
C) Środek okręgu opisanego na trójkącie to punkt przecięcia się dwusiecznych kątów trójkąta.
D) Środek okręgu opisanego na trójkącie to punkt przecięcia się wysokości trójkąta
Trójkąt 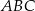 ma boki długości 4 cm, 13 cm, 15 cm oraz pole równe
ma boki długości 4 cm, 13 cm, 15 cm oraz pole równe 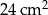 . Najdłuższa wysokość trójkąta
. Najdłuższa wysokość trójkąta 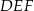 podobnego do trójkąta
podobnego do trójkąta 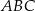 w skali 1:3 ma długość
w skali 1:3 ma długość
A) 4 cm B) 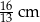 C) 2 cm D)
C) 2 cm D) 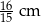
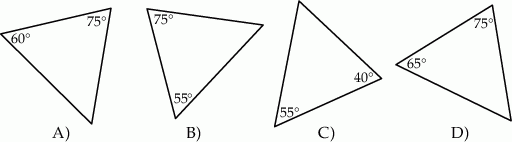
Który z narysowanych trójkątów jest podobny do trójkąta, w którym miary dwóch kątów wynoszą 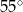 i
i 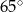 ?
?
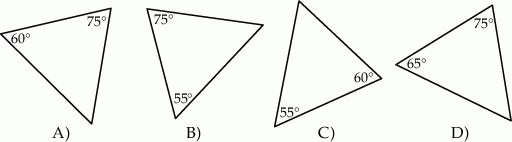
Który z narysowanych trójkątów jest podobny do trójkąta, w którym miary dwóch kątów wynoszą 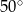 i
i 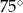 ?
?
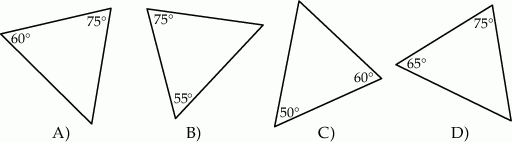
Który z narysowanych trójkątów jest podobny do trójkąta, w którym miary dwóch kątów wynoszą 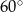 i
i 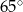 ?
?
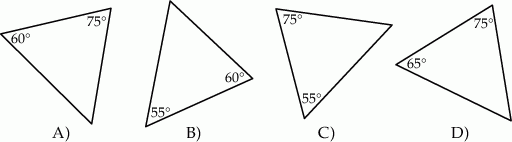
Który z narysowanych trójkątów jest podobny do trójkąta, w którym miary dwóch kątów wynoszą 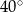 i
i 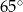 ?
?
Dane są dwa trójkąty podobne 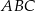 i
i 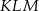 o polach równych – odpowiednio –
o polach równych – odpowiednio – 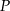 oraz
oraz 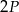 . Obwód trójkąta
. Obwód trójkąta 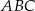 jest równy
jest równy  . Obwód trójkąta
. Obwód trójkąta 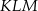 jest równy
jest równy
A) 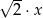 , , | B) 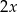 , , |
| ponieważ stosunek obwodów trójkątów podobnych jest równy | |
| 1) | kwadratowi stosunku pól tych trójkątów. |
| 2) | pierwiastkowi kwadratowemu ze stosunku pól tych trójkątów. |
| 3) | stosunkowi pól tych trójkątów. |
Dane są dwa trójkąty podobne 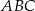 i
i 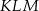 o polach równych – odpowiednio –
o polach równych – odpowiednio – 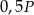 oraz
oraz 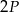 . Promień okręgu wpisanego w trójkąt
. Promień okręgu wpisanego w trójkąt 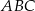 jest równy
jest równy  . Promień okręgu wpisanego w trójkąt
. Promień okręgu wpisanego w trójkąt 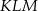 jest równy
jest równy
A) 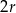 , , | B) 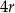 , , |
| ponieważ stosunek promieni okręgów wpisanych trójkątów podobnych jest równy | |
| 1) | pierwiastkowi kwadratowemu ze stosunku pól tych trójkątów. |
| 2) | kwadratowi stosunku pól tych trójkątów. |
| 3) | stosunkowi pól tych trójkątów. |
Środkowe w trójkącie 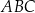 przecinają się w punkcie
przecinają się w punkcie 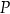 odległym od wierzchołka
odległym od wierzchołka 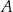 o 6 cm. Wobec tego środkowa poprowadzona na bok
o 6 cm. Wobec tego środkowa poprowadzona na bok 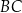 ma długość
ma długość
A) 12 cm B) 9 cm C) 15 cm D) 10 cm
Punkt 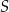 jest środkiem ciężkości trójkąta
jest środkiem ciężkości trójkąta 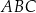 . Długość odcinka
. Długość odcinka 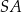 jest równa 10. Długość środkowej poprowadzonej z wierzchołka
jest równa 10. Długość środkowej poprowadzonej z wierzchołka 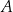 do boku
do boku 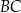 jest równa
jest równa
A) 10 B) 15 C) 20 D) 30
Środkowe w trójkącie 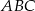 przecinają się w punkcie
przecinają się w punkcie 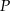 , przy czym długość środkowej opuszczonej na bok
, przy czym długość środkowej opuszczonej na bok 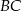 ma długość 9 cm. Wobec tego długość odcinka
ma długość 9 cm. Wobec tego długość odcinka 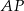 wynosi
wynosi
A) 6 cm B) 3 cm C) 2 cm D) 5 cm
Środkowe w trójkącie 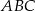 przecinają się w punkcie
przecinają się w punkcie 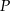 odległym od wierzchołka
odległym od wierzchołka 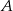 o 6 cm. Środkowa opuszczona na bok
o 6 cm. Środkowa opuszczona na bok 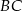 przecina ten bok w punkcie
przecina ten bok w punkcie 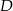 . Wobec tego długość odcinka
. Wobec tego długość odcinka 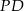 wynosi
wynosi
A) 1 cm B) 2 cm C) 3 cm D) 6 cm
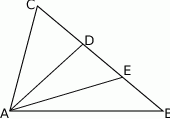
Punkty 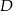 i
i 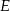 dzielą bok
dzielą bok 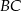 trójkąta
trójkąta 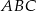 na trzy równe części (zobacz rysunek). Stosunek pól trójkątów
na trzy równe części (zobacz rysunek). Stosunek pól trójkątów 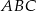 i
i 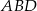 jest równy
jest równy
A)  B)
B)  C)
C)  D)
D) 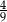
Okrąg jest styczny do boku 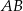 trójkąta
trójkąta 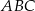 w punkcie
w punkcie 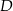 oraz przecina boki
oraz przecina boki 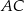 i
i 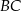 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 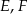 i
i 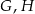 (zobacz rysunek). Kat
(zobacz rysunek). Kat 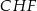 ma miarę
ma miarę 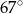 .
.
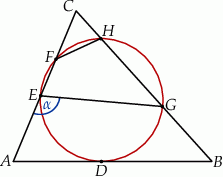
Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 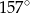 B)
B) 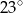 C)
C) 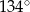 D)
D) 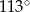
Okrąg jest styczny do boku 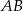 trójkąta
trójkąta 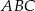 w punkcie
w punkcie 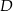 oraz przecina boki
oraz przecina boki 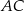 i
i 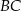 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 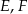 i
i 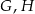 (zobacz rysunek). Kat
(zobacz rysunek). Kat 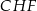 ma miarę
ma miarę 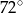 .
.
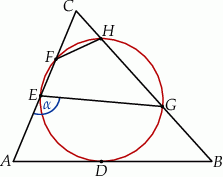
Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 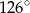 B)
B) 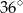 C)
C) 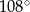 D)
D) 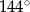
Połączono środki boków trójkąta 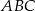 otrzymując trójkąt
otrzymując trójkąt 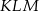 . O ile procent pole trójkąta
. O ile procent pole trójkąta 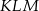 jest mniejsze od pola trójkąta
jest mniejsze od pola trójkąta 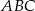 ?
?
A) 80% B) 75% C) 50% D) 25%
Obwody dwóch trójkątów podobnych, których pola pozostają w stosunku 1:4, mogą być równe
A) 9 i 36 B) 18 i 36 C) 9 i 144 D) 18 i 144
Pole trójkąta 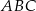 przedstawionego na rysunku jest równe
przedstawionego na rysunku jest równe
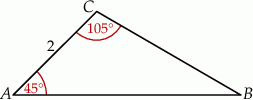
A) 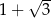 B)
B) 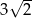 C)
C) 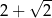 D)
D) 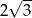
Kąty między bokiem trójkąta ostrokątnego a wysokościami opuszczonymi z należących do tego boku wierzchołków mają miary 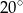 i
i 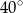 . Kąty tego trójkąta mają miary:
. Kąty tego trójkąta mają miary:
A) 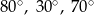 B)
B) 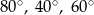 C)
C) 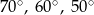 D)
D) 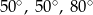
Kąty między bokiem trójkąta ostrokątnego a wysokościami opuszczonymi z należących do tego boku wierzchołków mają miary 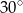 i
i 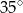 . Kąty tego trójkąta mają miary:
. Kąty tego trójkąta mają miary:
A) 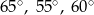 B)
B) 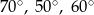 C)
C) 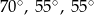 D)
D) 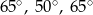
Dany jest trójkąt o bokach długości 4, 5 oraz 6. Cosinus największego kąta wewnętrznego tego trójkąta jest równy
A) 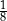 B)
B) 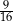 C)
C)  D)
D) 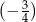
Oblicz długość odcinka 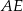 wiedząc, że
wiedząc, że 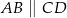 i
i 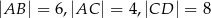 .
.
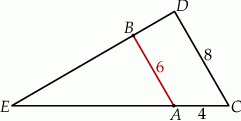
A) 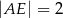 B)
B) 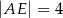 C)
C) 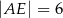 D)
D) 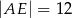
W trójkącie 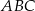 punkt
punkt 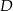 leży na boku
leży na boku 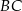 , a punkt
, a punkt 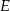 leży na boku
leży na boku 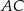 . Odcinek
. Odcinek 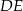 jest równoległy do boku
jest równoległy do boku 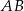 , a ponadto
, a ponadto 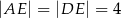 ,
, 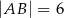 (zobacz rysunek).
(zobacz rysunek).
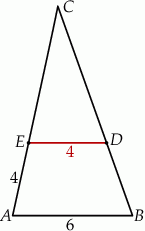
Odcinek 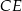 ma długość
ma długość
A) 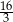 B)
B)  C) 8 D) 6
C) 8 D) 6
Odcinki 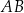 i
i 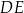 są równoległe. Długości odcinków
są równoległe. Długości odcinków 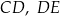 i
i 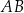 są odpowiednio równe 1, 3 i 9.
są odpowiednio równe 1, 3 i 9.
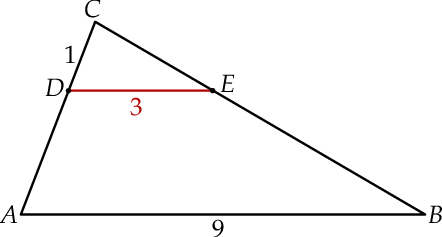
Długość odcinka 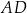 jest równa
jest równa
A) 2 B) 3 C) 5 D) 6
Odcinki 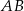 i
i 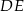 są równoległe. Długości odcinków
są równoległe. Długości odcinków 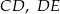 i
i 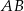 są odpowiednio równe 2, 4 i 16.
są odpowiednio równe 2, 4 i 16.
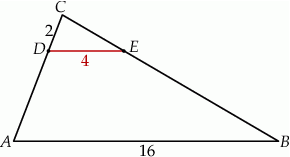
Długość odcinka 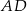 jest równa
jest równa
A) 12 B) 8 C) 3 D) 6
Odcinki 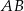 i
i 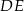 są równoległe. Długości odcinków
są równoległe. Długości odcinków 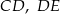 i
i 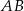 są odpowiednio równe 2, 5 i 15.
są odpowiednio równe 2, 5 i 15.
Długość odcinka 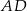 jest równa
jest równa
A) 3 B) 4 C) 5 D) 6
Jeżeli odcinki 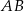 i
i 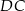 są równoległe, to długość odcinka
są równoległe, to długość odcinka 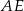 (patrz rys.) jest równa
(patrz rys.) jest równa
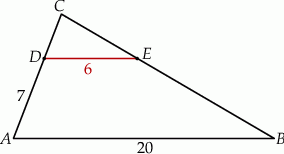
A) 9 B) 10 C) 11 D) 12
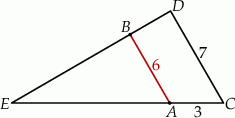
Oblicz długość odcinka 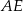 wiedząc, że
wiedząc, że 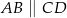 i
i 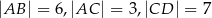 .
.
A) 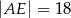 B)
B) 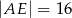 C)
C) 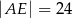 D)
D) 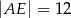
Oblicz długość odcinka 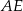 wiedząc, że
wiedząc, że 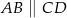 i
i 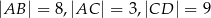 .
.
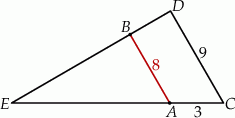
A) 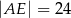 B)
B) 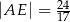 C)
C) 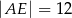 D)
D) 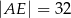
W trójkącie 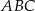 punkt
punkt 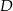 leży na boku
leży na boku 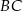 , a punkt
, a punkt 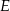 leży na boku
leży na boku 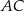 . Odcinek
. Odcinek 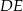 jest równoległy do boku
jest równoległy do boku 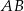 , a ponadto
, a ponadto 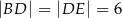 ,
, 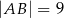 (zobacz rysunek).
(zobacz rysunek).
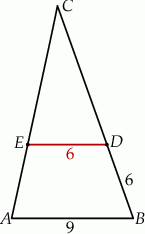
Odcinek 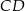 ma długość
ma długość
A) 8 B) 4 C) 9 D) 12
Oblicz długość odcinka 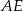 wiedząc, że
wiedząc, że 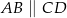 i
i 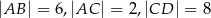 .
.
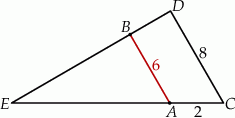
A) 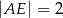 B)
B) 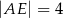 C)
C) 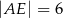 D)
D) 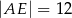
W trójkącie 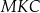 bok
bok 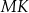 ma długość 24. Prosta równoległa do boku
ma długość 24. Prosta równoległa do boku 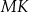 przecina boki
przecina boki 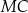 i
i 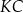 – odpowiednio – w punktach
– odpowiednio – w punktach 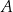 oraz
oraz 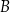 takich, że
takich, że 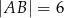 i
i 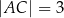 (zobacz rysunek).
(zobacz rysunek).

Długość odcinka 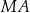 jest równa
jest równa
A) 18 B) 15 C) 9 D) 12
Punkt 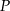 jest punktem wspólnym środkowych
jest punktem wspólnym środkowych 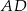 i
i 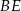 w trójkącie
w trójkącie 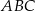 . Wówczas odcinki
. Wówczas odcinki 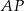 i
i 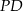 mogą mieć długości
mogą mieć długości
A) 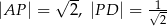 B)
B) 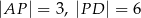
C) 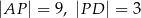 D)
D) 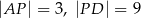
W trójkącie zwiększono długość każdego boku o 20%. O ile procent wzrosło pole tego trójkąta?
A) 20% B) 40% C) 44% D) 400%
Pole trójkąta 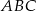 wynosi
wynosi 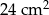 . Połączono środki boków tego trójkąta i otrzymano trójkąt
. Połączono środki boków tego trójkąta i otrzymano trójkąt 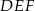 , którego pole jest równe
, którego pole jest równe
A) 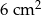 B)
B) 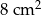 C)
C) 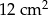 D)
D) 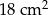
Sinusy dwóch kątów ostrych trójkąta są odpowiednio równe 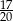 i
i 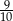 . Jeżeli
. Jeżeli  jest miarą najmniejszego kąta tego trójkąta, to
jest miarą najmniejszego kąta tego trójkąta, to
A) 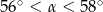 B)
B) 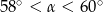 C)
C) 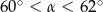 D)
D)