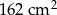Jeżeli trójkąty 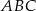 i
i 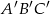 są podobne, a ich obwody są odpowiednio równe 25 cm i 50 cm, to skala podobieństwa trójkątów
są podobne, a ich obwody są odpowiednio równe 25 cm i 50 cm, to skala podobieństwa trójkątów 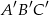 i
i 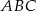 jest równa
jest równa
A) 2 B) 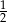 C)
C) 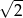 D)
D) 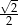
/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt/Dowolny
Pole trójkąta 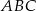 jest cztery razy mniejsze od pola trójkąta
jest cztery razy mniejsze od pola trójkąta 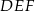 . Trójkąty te są podobne. Długość boku
. Trójkąty te są podobne. Długość boku 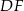 jest równa 16. Długość boku
jest równa 16. Długość boku 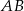 , odpowiadającego bokowi
, odpowiadającego bokowi 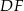 , jest równa
, jest równa
A) 64 B) 32 C) 4 D) 8
Pole trójkąta 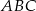 jest cztery razy większe od pola trójkąta
jest cztery razy większe od pola trójkąta 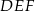 . Trójkąty te są podobne. Długość boku
. Trójkąty te są podobne. Długość boku 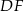 jest równa 16. Długość boku
jest równa 16. Długość boku 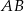 , odpowiadającego bokowi
, odpowiadającego bokowi 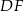 , jest równa
, jest równa
A) 64 B) 32 C) 4 D) 8
Pole trójkąta 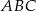 jest dziewięć razy mniejsze od pola trójkąta
jest dziewięć razy mniejsze od pola trójkąta 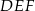 . Trójkąty te są podobne. Długość boku
. Trójkąty te są podobne. Długość boku 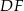 jest równa 9. Długość boku
jest równa 9. Długość boku 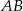 , odpowiadającego bokowi
, odpowiadającego bokowi 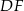 , jest równa
, jest równa
A) 81 B) 27 C) 3 D) 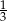
Trójkąty 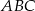 i
i 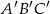 są podobne
są podobne 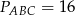 ,
, 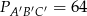 , wysokość
, wysokość 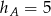 . Odpowiadająca jej wysokość w drugim trójkącie jest równa:
. Odpowiadająca jej wysokość w drugim trójkącie jest równa:
A) 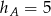 B)
B) 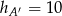 C)
C) 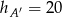 D) nie można określić
D) nie można określić
Dany jest trójkąt o bokach długości 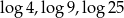 . Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
. Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
A) 2, 3, 5 B) 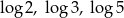 C)
C) 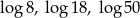 D) 4, 9, 25
D) 4, 9, 25
Pole trójkąta 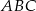 jest równe 17, a jego obwód 22. Jaki jest obwód trójkąta o polu 68, podobnego do trójkąta
jest równe 17, a jego obwód 22. Jaki jest obwód trójkąta o polu 68, podobnego do trójkąta 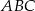 ?
?
A) 34 B) 44 C) 51 D) 88
Trójkąty 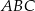 oraz
oraz 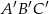 są podobne. Obwód trójkąta
są podobne. Obwód trójkąta 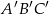 jest równy 12, a jego pole 6. Jeżeli pole trójkąta
jest równy 12, a jego pole 6. Jeżeli pole trójkąta 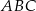 jest równe
jest równe 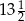 , to jego obwód wynosi
, to jego obwód wynosi
A) 18 B) 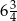 C) 27 D) 9
C) 27 D) 9
Dany jest trójkąt 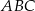 , w którym
, w którym 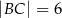 . Miara kąta
. Miara kąta 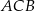 jest równa
jest równa 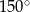 (zobacz rysunek).
(zobacz rysunek).
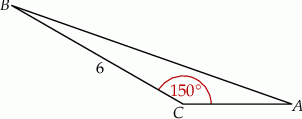
Wysokość trójkąta 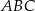 opuszczona z wierzchołka
opuszczona z wierzchołka 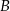 jest równa
jest równa
A) 3 B) 4 C) 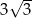 D)
D) 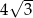
Jeden kąt trójkąta ma miarę 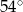 . Z pozostałych dwóch kątów tego trójkąta jeden jest 6 razy większy od drugiego. Miary pozostałych kątów są równe
. Z pozostałych dwóch kątów tego trójkąta jeden jest 6 razy większy od drugiego. Miary pozostałych kątów są równe
A) 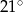 i
i 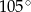 B)
B) 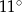 i
i 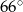 C)
C) 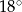 i
i 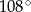 D)
D) 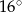 i
i 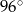
Jeden kąt trójkąta ma miarę 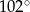 . Z pozostałych dwóch kątów tego trójkąta jeden jest 5 razy większy od drugiego. Miary pozostałych kątów są równe
. Z pozostałych dwóch kątów tego trójkąta jeden jest 5 razy większy od drugiego. Miary pozostałych kątów są równe
A) 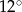 i
i 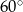 B)
B) 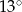 i
i 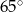 C)
C) 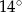 i
i 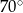 D)
D) 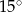 i
i 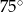
Jeden z kątów wewnętrznych trójkąta ma 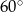 , a miary dwóch pozostałych kątów pozostają w stosunku jak 1:4. Miara kąta rozwartego tego trójkąta wynosi
, a miary dwóch pozostałych kątów pozostają w stosunku jak 1:4. Miara kąta rozwartego tego trójkąta wynosi
A) 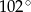 B)
B) 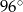 C)
C) 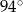 D)
D) 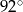
Dany jest trójkąt 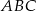 , w którym
, w którym 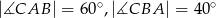 . Odcinki
. Odcinki 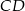 i
i 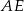 są dwusiecznymi kątów przy wierzchołkach
są dwusiecznymi kątów przy wierzchołkach 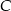 i
i 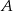 tego trójkąta. Zatem kąt
tego trójkąta. Zatem kąt  zaznaczony na rysunku ma miarę:
zaznaczony na rysunku ma miarę:
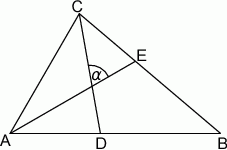
A) 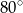 B)
B) 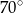 C)
C) 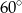 D)
D) 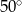
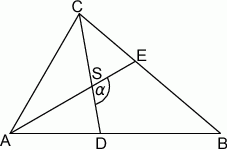
Dany jest trójkąt 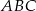 , w którym
, w którym 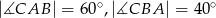 . Odcinki
. Odcinki 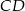 i
i 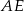 są dwusiecznymi kątów przy wierzchołkach
są dwusiecznymi kątów przy wierzchołkach 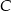 i
i 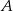 tego trójkąta. Zatem kąt
tego trójkąta. Zatem kąt  zaznaczony na rysunku ma miarę:
zaznaczony na rysunku ma miarę:
A) 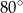 B)
B) 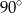 C)
C) 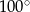 D)
D) 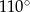
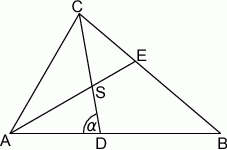
Dany jest trójkąt 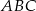 , w którym
, w którym 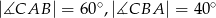 . Odcinki
. Odcinki 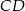 i
i 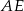 są dwusiecznymi kątów przy wierzchołkach
są dwusiecznymi kątów przy wierzchołkach 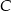 i
i 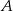 tego trójkąta. Zatem kąt
tego trójkąta. Zatem kąt  zaznaczony na rysunku ma miarę:
zaznaczony na rysunku ma miarę:
A) 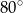 B)
B) 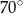 C)
C) 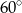 D)
D) 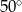
Punkty 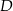 ,
, 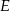 i
i 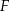 są punktami styczności okręgu wpisanego w trójkąt
są punktami styczności okręgu wpisanego w trójkąt 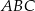 z jego bokami i
z jego bokami i 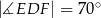 (zobacz rysunek).
(zobacz rysunek).
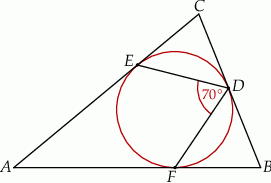
Miara kąta 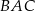 jest równa
jest równa
A) 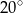 B)
B) 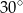 C)
C) 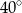 D)
D) 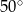
W trójkącie 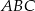 miary kątów wynoszą:
miary kątów wynoszą: 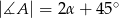 ,
, 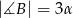 ,
, 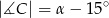 . Wówczas
. Wówczas
A) 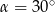 B)
B) 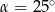 C)
C) 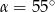 D)
D) 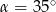
W trójkącie 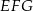 bok
bok 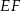 ma długość 21. Prosta równoległa do boku
ma długość 21. Prosta równoległa do boku 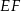 przecina boki
przecina boki 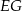 i
i 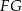 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 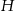 oraz
oraz 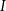 (zobacz rysunek) w taki sposób, że
(zobacz rysunek) w taki sposób, że 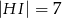 i
i 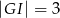 . Wtedy długość odcinka
. Wtedy długość odcinka 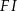 jest równa
jest równa
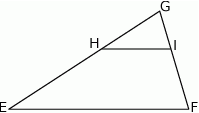
A) 6 B) 9 C) 12 D) 17
W trójkącie 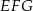 bok
bok 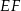 ma długość 24. Prosta równoległa do boku
ma długość 24. Prosta równoległa do boku 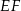 przecina boki
przecina boki 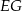 i
i 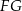 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 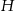 oraz
oraz 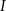 (zobacz rysunek) w taki sposób, że
(zobacz rysunek) w taki sposób, że 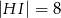 i
i 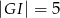 . Wtedy długość odcinka
. Wtedy długość odcinka 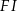 jest równa
jest równa
A) 6 B) 9 C) 10 D) 12
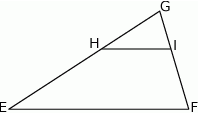
Odcinki 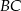 i
i 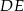 są równoległe i
są równoległe i 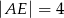 ,
, 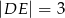 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 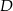 jest środkiem odcinka
jest środkiem odcinka 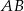 . Długość odcinka
. Długość odcinka 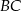 jest równa
jest równa
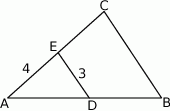
A) 4 B) 6 C) 8 D) 16
Odcinki 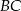 i
i 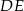 są równoległe i
są równoległe i 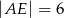 ,
, 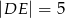 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 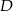 jest środkiem odcinka
jest środkiem odcinka 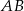 . Długość odcinka
. Długość odcinka 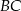 jest równa
jest równa
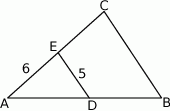
A) 10 B) 6 C) 8 D) 30
Długości boków trójkąta  są równe 10 cm, 11 cm, 15 cm. Zatem
są równe 10 cm, 11 cm, 15 cm. Zatem
A) trójkąt ten jest ostrokątny
B) trójkąt ten jest prostokątny
C) trójkąt ten jest rozwartokątny
D) jest zbyt mało danych aby określić jakiego rodzaju jest to trójkąt
Długości boków trójkąta  są równe 10 cm, 12 cm, 15 cm. Zatem
są równe 10 cm, 12 cm, 15 cm. Zatem
A) trójkąt ten jest ostrokątny
B) trójkąt ten jest prostokątny
C) trójkąt ten jest rozwartokątny
D) jest zbyt mało danych aby określić jakiego rodzaju jest to trójkąt
Długości boków trójkąta  są równe 8 cm, 15 cm, 17 cm. Zatem
są równe 8 cm, 15 cm, 17 cm. Zatem
A) trójkąt ten jest ostrokątny
B) trójkąt ten jest prostokątny
C) trójkąt ten jest rozwartokątny
D) jest zbyt mało danych aby określić jakiego rodzaju jest to trójkąt
Dany jest trójkąt 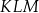 , w którym
, w którym 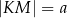 ,
, 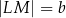 oraz
oraz 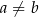 . Dwusieczna kąta
. Dwusieczna kąta 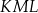 przecina bok
przecina bok 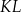 w punkcie
w punkcie 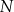 takim, że
takim, że 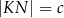 ,
, 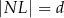 oraz
oraz 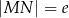 (zobacz rysunek).
(zobacz rysunek).

W trójkącie 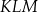 prawdziwa jest równość
prawdziwa jest równość
A) 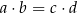 B)
B) 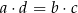 C)
C) 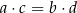 D)
D) 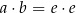
Nie jest prawdziwe zdanie
A) Środek ciężkości trójkąta to punkt przecięcia się wysokości trójkąta.
B) Środek okręgu wpisanego w trójkąt to punkt przecięcia się dwusiecznych kątów trójkąta.
C) Środek okręgu opisanego na trójkącie to punkt przecięcia się symetralnych boków trójkąta.
D) Środkowe trójkąta dzielą się w stosunku 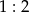 .
.
Nie jest prawdziwe zdanie
A) Środek ciężkości trójkąta to punkt przecięcia się środkowych trójkąta.
B) Środek okręgu wpisanego w trójkąt to punkt przecięcia się dwusiecznych kątów trójkąta.
C) Środek okręgu opisanego na trójkącie to punkt przecięcia się symetralnych boków trójkąta.
D) Środkowe trójkąta dzielą się w stosunku 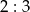 .
.
Nie jest prawdziwe zdanie
A) Środek ciężkości trójkąta to punkt przecięcia się środkowych trójkąta.
B) Środek okręgu wpisanego w trójkąt to punkt przecięcia się dwusiecznych kątów trójkąta.
C) Środek okręgu opisanego na trójkącie to punkt przecięcia się wysokości trójkąta.
D) Środkowe trójkąta dzielą się w stosunku 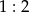 .
.
Przedstawione na rysunku trójkąty są podobne.
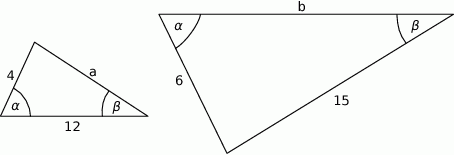
Wówczas
A) 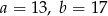 B)
B) 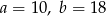 C)
C) 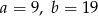 D)
D) 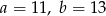
Przedstawione na rysunku trójkąty 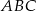 i
i 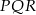 są podobne. Bok
są podobne. Bok 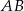 trójkąta
trójkąta 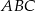 ma długość
ma długość
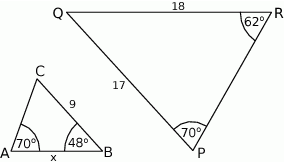
A) 8 B) 8,5 C) 9,5 D) 10
Przedstawione na rysunku trójkąty 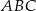 i
i 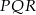 są podobne. Bok
są podobne. Bok 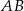 trójkąta
trójkąta 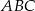 ma długość
ma długość
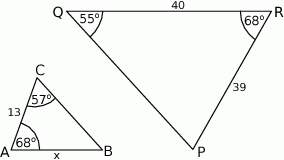
A) 14 B) 16 C) 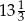 D) 12
D) 12
Dany jest trójkąt 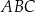 , w którym
, w którym 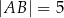 ,
, 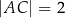 oraz
oraz 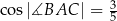 . Długość boku
. Długość boku 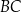 tego trójkąta jest równa
tego trójkąta jest równa
A) 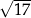 B)
B) 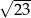 C)
C) 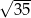 D)
D) 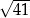
Boki trójkąta 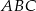 mają długości 12 cm, 15 cm, 18 cm. Trójkąt
mają długości 12 cm, 15 cm, 18 cm. Trójkąt 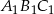 jest podobny do trójkąta
jest podobny do trójkąta 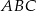 . Najdłuższy bok trójkąta
. Najdłuższy bok trójkąta 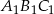 ma długość 6 cm. Obwód trójkąta
ma długość 6 cm. Obwód trójkąta 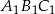 jest równy
jest równy
A) 15 cm B) 45 cm C) 22,5 cm D) 9 cm
Z trójkąta 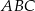 o obwodzie 50 wycięto kwadrat
o obwodzie 50 wycięto kwadrat 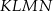 o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
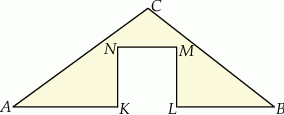
A) 64 B) 60 C) 75 D) 70
Długości boków trójkąta wychodzących z wierzchołka kąta ostrego  wynoszą odpowiednio 2 dm i 40 cm. Jaką miarę ma kąt
wynoszą odpowiednio 2 dm i 40 cm. Jaką miarę ma kąt  , jeśli pole tego trójkąta jest równe
, jeśli pole tego trójkąta jest równe 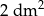 ?
?
A) 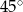 B)
B) 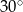 C)
C) 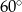 D)
D) 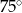
Obrazem trójkąta 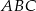 w podobieństwie o skali
w podobieństwie o skali 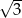 jest trójkąt
jest trójkąt 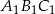 . Pole trójkąta
. Pole trójkąta 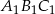 wynosi
wynosi 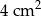 . Zatem pole trójkąta
. Zatem pole trójkąta 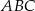 jest równe
jest równe
A) 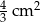 B)
B) 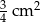 C)
C) 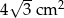 D)
D) 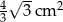
Obrazem trójkąta 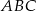 w podobieństwie o skali
w podobieństwie o skali 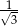 jest trójkąt
jest trójkąt 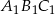 . Pole trójkąta
. Pole trójkąta 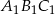 wynosi
wynosi 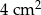 . Zatem pole trójkąta
. Zatem pole trójkąta 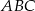 jest równe
jest równe
A) 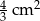 B)
B) 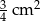 C)
C) 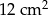 D)
D) 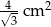
Obrazem trójkąta 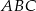 w podobieństwie o skali
w podobieństwie o skali 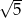 jest trójkąt
jest trójkąt 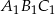 . Pole trójkąta
. Pole trójkąta 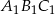 wynosi
wynosi 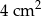 . Zatem pole trójkąta
. Zatem pole trójkąta 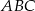 jest równe
jest równe
A) 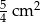 B)
B) 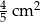 C)
C) 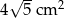 D)
D) 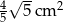
Trójkąt 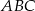 jest podobny do trójkąta
jest podobny do trójkąta 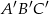 w skali
w skali  , przy czym
, przy czym 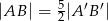 . Stosunek pola trójkąta
. Stosunek pola trójkąta 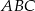 do pola trójkąta
do pola trójkąta 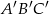 jest równy
jest równy
A) 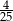 B)
B)  C)
C)  D)
D) 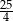
Pole trójkąta 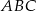 jest równe
jest równe 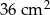 . Trójkąt
. Trójkąt 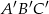 jest podobny do trójkąta
jest podobny do trójkąta 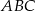 w skali
w skali 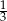 . Pole trójkąta
. Pole trójkąta 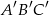 jest równe
jest równe
A) 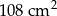 B)
B) 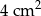 C)
C) 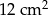 D)
D) 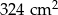
Pole trójkąta 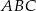 jest równe
jest równe 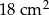 . Trójkąt
. Trójkąt 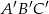 jest podobny do trójkąta
jest podobny do trójkąta 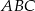 w skali
w skali 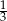 . Pole trójkąta
. Pole trójkąta 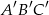 jest równe
jest równe
A) 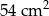 B)
B) 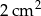 C)
C) 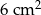 D)
D)