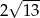Punkt 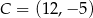 jest wierzchołkiem trójkąta równoramiennego, którego podstawa
jest wierzchołkiem trójkąta równoramiennego, którego podstawa 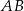 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 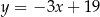 . Wysokość opuszczona na podstawę
. Wysokość opuszczona na podstawę 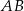 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu
A) 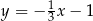 B)
B) 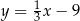 C)
C) 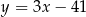 D)
D) 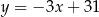
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Trójkąt
Dany jest trójkąt  , w którym
, w którym 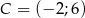 ,
, ![−→ CB = [4;− 2]](https://img.zadania.info/zad/8646781/HzadT2x.gif) oraz środek ciężkości
oraz środek ciężkości 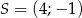 . Współrzędne wierzchołka
. Współrzędne wierzchołka 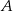 są równe
są równe
A) 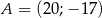 B)
B) 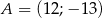 C)
C) 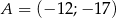 D)
D) 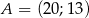
Punkt przecięcia środkowych w trójkącie 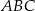 , gdzie
, gdzie 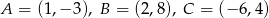 ma współrzędne:
ma współrzędne:
A) 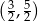 B)
B) 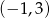 C)
C) 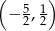 D)
D) 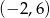
Na płaszczyźnie dane są punkty: 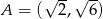 ,
, 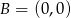 i
i 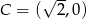 . Kąt
. Kąt 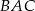 jest równy
jest równy
A) 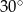 B)
B) 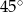 C)
C) 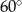 D)
D) 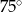
Na płaszczyźnie dane są punkty: 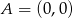 ,
, 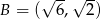 i
i 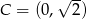 . Kąt
. Kąt 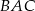 jest równy
jest równy
A) 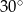 B)
B) 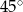 C)
C) 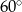 D)
D) 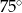
Na płaszczyźnie dane są punkty: 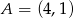 ,
, 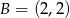 i
i 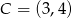 . Kąt
. Kąt 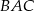 jest równy
jest równy
A) 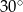 B)
B) 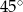 C)
C) 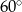 D)
D) 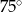
Pole trójkąta wyznaczonego przez wykresy funkcji 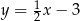 i
i 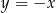 oraz oś
oraz oś 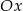 jest równe
jest równe
A) 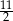 B)
B) 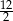 C)
C) 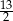 D)
D) 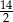
Pole trójkąta wyznaczonego przez wykresy funkcji 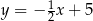 i
i 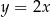 oraz oś
oraz oś 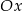 jest równe
jest równe
A) 20 B) 10 C) 32 D) 40
W trójkącie  dane są wierzchołki
dane są wierzchołki 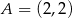 ,
, 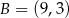 ,
, 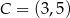 . Trójkąt
. Trójkąt 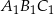 jest obrazem trójkąta
jest obrazem trójkąta 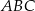 w jednokładności o środku
w jednokładności o środku 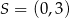 i skali
i skali 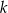 . Trójkąty te leżą po przeciwnych stronach osi rzędnych. Promień okręgu opisanego na trójkącie
. Trójkąty te leżą po przeciwnych stronach osi rzędnych. Promień okręgu opisanego na trójkącie 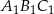 ma długość
ma długość 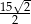 . Skala jednokładności
. Skala jednokładności 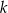 wynosi
wynosi
A) 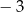 B)
B) 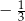 C)
C) 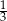 D) 3
D) 3
Punkt 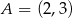 jest wierzchołkiem trójkąta równobocznego
jest wierzchołkiem trójkąta równobocznego 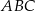 . Punkt
. Punkt 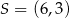 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 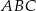 . Wskaż równanie okręgu wpisanego w trójkąt
. Wskaż równanie okręgu wpisanego w trójkąt 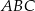 .
.
A) 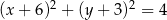 B)
B) 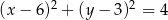
C) 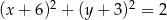 D)
D) 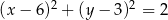
Punkt 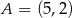 jest wierzchołkiem trójkąta równobocznego
jest wierzchołkiem trójkąta równobocznego 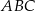 . Punkt
. Punkt 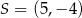 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 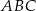 . Wskaż równanie okręgu wpisanego w trójkąt
. Wskaż równanie okręgu wpisanego w trójkąt  .
.
A) 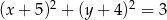 B)
B) 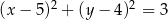
C) 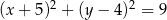 D)
D) 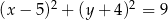
Punkty 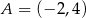 i
i 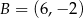 są końcami podstawy trójkąta równoramiennego
są końcami podstawy trójkąta równoramiennego 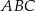 . Prosta zawierająca wysokość
. Prosta zawierająca wysokość 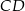 tego trójkąta przecina prostą
tego trójkąta przecina prostą 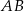 w punkcie
w punkcie
A) 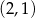 B)
B) 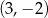 C)
C) 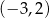 D)
D) 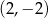
Punkty 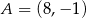 i
i 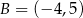 są końcami podstawy trójkąta równoramiennego
są końcami podstawy trójkąta równoramiennego 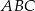 . Prosta zawierająca wysokość
. Prosta zawierająca wysokość 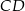 tego trójkąta przecina prostą
tego trójkąta przecina prostą 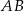 w punkcie
w punkcie
A) 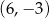 B)
B) 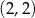 C)
C) 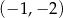 D)
D) 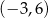
Punkt 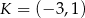 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 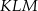 , w którym
, w którym 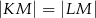 . Odcinek
. Odcinek 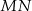 jest wysokością trójkąta i
jest wysokością trójkąta i 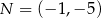 . Zatem
. Zatem
A) 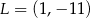 B)
B) 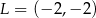 C)
C) 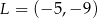 D)
D) 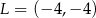
Punkt 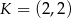 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 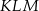 , w którym
, w którym 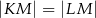 . Odcinek
. Odcinek 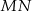 jest wysokością trójkąta i
jest wysokością trójkąta i 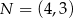 . Zatem
. Zatem
A) 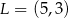 B)
B) 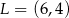 C)
C) 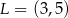 D)
D) 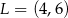
Punkt 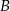 jest symetryczny do punktu
jest symetryczny do punktu 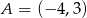 względem osi
względem osi  układu współrzędnych, a punkt
układu współrzędnych, a punkt 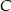 jest symetryczny do punktu
jest symetryczny do punktu 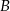 względem osi
względem osi 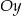 . Zatem trójkąt
. Zatem trójkąt 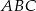 jest
jest
A) równoboczny
B) prostokątny i równoramienny
C) prostokątny i żaden z jego kątów nie jest równy 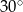
D) prostokątny z kątem ostrym równym 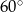
Wierzchołki trójkąta 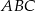 mają współrzędne
mają współrzędne 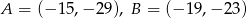 i
i 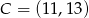 . Bok
. Bok 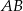 trójkąta
trójkąta 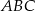 ma długość
ma długość
A) 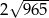 B)
B) 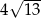 C)
C) 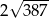 D)
D)