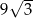Dany jest trójkąt o wierzchołkach 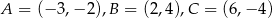 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 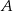 jest równa
jest równa
A) 4 B) 6 C) 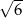 D)
D) 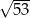
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Trójkąt
Dany jest trójkąt o wierzchołkach 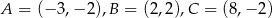 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 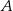 jest równa
jest równa
A) 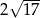 B)
B) 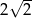 C)
C) 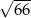 D)
D) 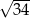
Dany jest trójkąt o wierzchołkach 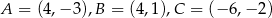 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 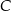 jest równa
jest równa
A) 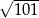 B)
B) 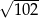 C)
C) 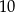 D)
D) 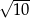
Dany jest trójkąt o wierzchołkach 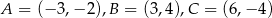 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 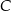 jest równa
jest równa
A) 11 B) 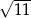 C)
C) 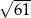 D)
D) 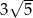
Dane są punkty 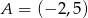 oraz
oraz 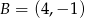 . Promień okręgu opisanego na trójkącie równobocznym
. Promień okręgu opisanego na trójkącie równobocznym 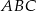 jest równy
jest równy
A) 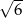 B)
B) 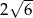 C)
C) 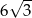 D)
D) 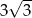
Punkty 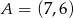 i
i 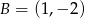 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 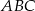 . Promień koła opisanego na tym trójkącie jest równy
. Promień koła opisanego na tym trójkącie jest równy
A) 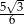 B)
B) 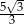 C)
C) 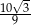 D)
D) 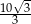
Punkty 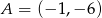 i
i 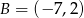 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 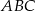 . Promień koła opisanego na tym trójkącie jest równy
. Promień koła opisanego na tym trójkącie jest równy
A) 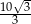 B)
B) 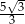 C)
C) 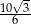 D)
D) 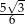
Podstawa 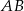 trójkąta
trójkąta 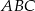 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 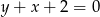 , a wierzchołek
, a wierzchołek 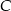 ma współrzędne
ma współrzędne 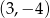 . Wysokość trójkąta opuszczona z wierzchołka
. Wysokość trójkąta opuszczona z wierzchołka 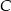 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu
A) 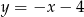 B)
B) 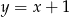 C)
C) 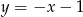 D)
D) 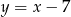
Punkt 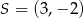 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 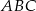 . Prosta zawierająca bok
. Prosta zawierająca bok 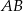 tego trójkąta ma równanie
tego trójkąta ma równanie 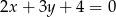 . Prosta zawierająca bok
. Prosta zawierająca bok 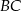 może mieć równanie
może mieć równanie
A) 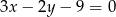 B)
B) 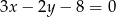 C)
C) 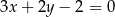 D)
D) 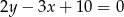
Punkt 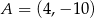 oraz jego rzuty prostokątne na osie układu współrzędnych są wierzchołkami trójkąta prostokątnego. Prosta zawierająca przeciwprostokątną tego trójkąta jest określona równaniem
oraz jego rzuty prostokątne na osie układu współrzędnych są wierzchołkami trójkąta prostokątnego. Prosta zawierająca przeciwprostokątną tego trójkąta jest określona równaniem
A) 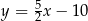 B)
B) 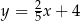 C)
C) 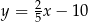 D)
D) 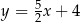
W trójkąt równoboczny wpisano okrąg o równaniu 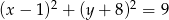 . Wysokość tego trójkąta ma długość
. Wysokość tego trójkąta ma długość
A) 9 B) 27 C) 4,5 D) 1
W trójkąt równoboczny wpisano okrąg o równaniu 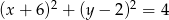 . Wysokość tego trójkąta ma długość
. Wysokość tego trójkąta ma długość
A) 12 B) 6 C) 8 D) 4
W trójkąt równoboczny wpisano okrąg o równaniu 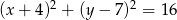 . Wysokość tego trójkąta ma długość
. Wysokość tego trójkąta ma długość
A) 48 B) 32 C) 24 D) 12
Pole trójkąta 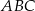 o wierzchołkach
o wierzchołkach 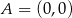 ,
, 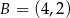 ,
, 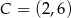 jest równe
jest równe
A) 5 B) 10 C) 15 D) 20
Pole trójkąta 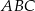 o wierzchołkach
o wierzchołkach 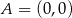 ,
, 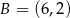 ,
, 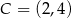 jest równe
jest równe
A) 10 B) 5 C) 20 D) 15
Na bokach 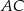 i
i 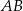 trójkąta
trójkąta  o wierzchołkach
o wierzchołkach 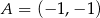 ,
, 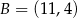 i
i 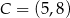 , wybrano punkty
, wybrano punkty 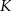 i
i 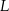 odpowiednio, w ten sposób, że
odpowiednio, w ten sposób, że 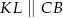 . Pole trapezu
. Pole trapezu 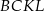 stanowi
stanowi 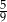 pola trójkąta
pola trójkąta 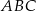 . Zatem
. Zatem
A) 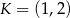 B)
B) 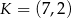 C)
C) 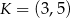 D)
D) 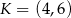
Punkty 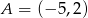 i
i 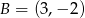 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 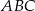 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 30 B) 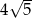 C)
C) 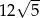 D) 36
D) 36
Punkty 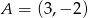 i
i 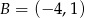 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 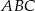 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 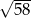 B)
B) 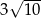 C)
C) 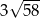 D)
D) 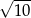
Punkty 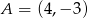 i
i 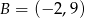 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 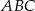 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 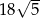 B)
B) 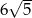 C) 45 D) 54
C) 45 D) 54
Punkty 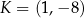 oraz
oraz 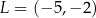 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 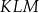 . Pole trójkąta
. Pole trójkąta 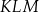 jest równe
jest równe
A) 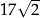 B)
B) 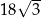 C)
C) 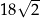 D)
D) 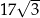
Punkty 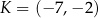 oraz
oraz 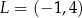 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 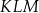 . Pole trójkąta
. Pole trójkąta 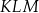 jest równe
jest równe
A) 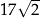 B)
B) 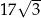 C)
C) 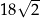 D)
D) 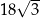
Punkty 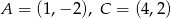 są dwoma wierzchołkami trójkąta równobocznego
są dwoma wierzchołkami trójkąta równobocznego 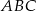 . Wysokość tego trójkąta jest równa
. Wysokość tego trójkąta jest równa
A) 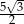 B)
B) 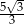 C)
C) 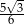 D)
D) 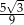
Punkty 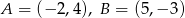 są dwoma wierzchołkami trójkąta równobocznego
są dwoma wierzchołkami trójkąta równobocznego 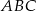 . Wysokość tego trójkąta jest równa
. Wysokość tego trójkąta jest równa
A) 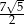 B)
B) 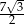 C)
C) 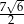 D)
D) 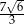
Punkty 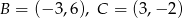 są dwoma wierzchołkami trójkąta równobocznego
są dwoma wierzchołkami trójkąta równobocznego 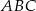 . Wysokość tego trójkąta jest równa
. Wysokość tego trójkąta jest równa
A) 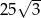 B)
B) 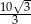 C)
C) 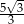 D)
D) 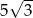
W okrąg o równaniu 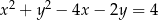 wpisano trójkąt równoramienny, w którym ramię tworzy z podstawą kąt o mierze
wpisano trójkąt równoramienny, w którym ramię tworzy z podstawą kąt o mierze 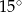 . Podstawa tego trójkąta ma długość
. Podstawa tego trójkąta ma długość
A) 1,5 B) 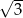 C) 3 D)
C) 3 D) 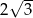
Dane są punkty 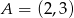 oraz
oraz 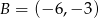 . Promień okręgu wpisanego w trójkąt równoboczny
. Promień okręgu wpisanego w trójkąt równoboczny 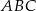 jest równy
jest równy
A) 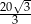 B)
B) 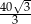 C)
C) 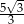 D)
D) 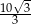
Punkty 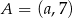 ,
, 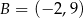 i
i 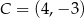 są wierzchołkami trójkąta równoramiennego o podstawie
są wierzchołkami trójkąta równoramiennego o podstawie 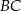 . Zatem
. Zatem
A) 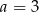 B)
B) 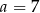 C)
C) 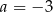 D)
D) 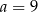
W układzie współrzędnych dany jest trójkąt o wierzchołkach 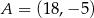 ,
, 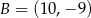 i
i 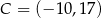 . Na boku
. Na boku 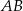 tego trójkąta wybrano punkt
tego trójkąta wybrano punkt 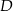 tak, że pole trójkąta
tak, że pole trójkąta 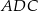 jest cztery razy mniejsze od pola trójkąta
jest cztery razy mniejsze od pola trójkąta 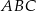 . Wówczas
. Wówczas
A) 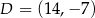 B)
B) 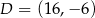 C)
C) 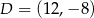 D)
D) 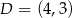
Punkty 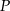 i
i 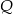 są środkami boków
są środkami boków 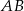 i
i 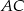 trójkąta
trójkąta 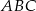 . Bok
. Bok 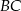 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu 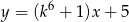 , a punkty
, a punkty 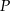 i
i 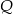 leżą na prostej
leżą na prostej 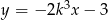 . Wynika stąd, że
. Wynika stąd, że
A) 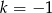 B)
B) 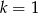 C)
C) 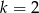 D)
D) 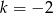
Wiadomo, że 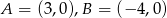 i punkty
i punkty 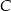 i
i 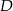 leżą na prostej
leżą na prostej 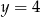 . Pole trójkąta
. Pole trójkąta 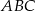 jest równe
jest równe 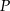 , a pole trójkąta
, a pole trójkąta 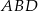 jest równe
jest równe 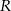 . Zatem
. Zatem
A) 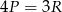 B)
B) 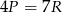 C)
C) 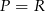 D)
D) 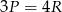
Wiadomo, że 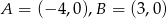 i punkty
i punkty 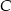 i
i 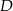 leżą na prostej
leżą na prostej 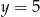 . Pole trójkąta
. Pole trójkąta 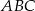 jest równe
jest równe 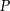 , a pole trójkąta
, a pole trójkąta 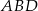 jest równe
jest równe 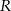 . Zatem
. Zatem
A) 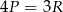 B)
B) 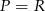 C)
C) 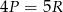 D)
D) 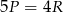
Wiadomo, że 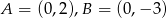 , a punkty
, a punkty 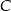 i
i 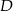 leżą na prostej
leżą na prostej 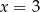 . Pole trójkąta
. Pole trójkąta 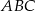 jest równe
jest równe 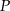 , a pole trójkąta
, a pole trójkąta 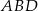 jest równe
jest równe 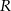 . Zatem
. Zatem
A) 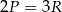 B)
B) 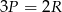 C)
C) 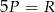 D)
D) 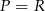
Prosta 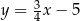 jest osią symetrii trójkąta
jest osią symetrii trójkąta 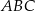 , w którym
, w którym 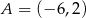 i
i 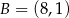 . Bok
. Bok 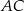 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu
A) 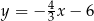 B)
B) 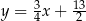 C)
C) 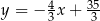 D)
D) 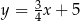
Dane są punkty 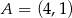 ,
, 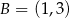 ,
, 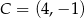 . Pole trójkąta
. Pole trójkąta 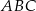 jest równe
jest równe
A) 3 B) 6 C) 8 D) 16
Dane są punkty 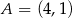 ,
, 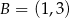 ,
, 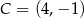 . Pole trójkąta
. Pole trójkąta 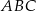 jest równe
jest równe
A) 2 B) 3 C) 6 D) 12
Punkty 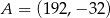 ,
, 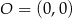 i
i 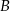 są wierzchołkami trójkąta prostokątnego o przeciwprostokątnej
są wierzchołkami trójkąta prostokątnego o przeciwprostokątnej 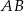 . Wskaż równanie prostej zawierającej przyprostokątną
. Wskaż równanie prostej zawierającej przyprostokątną 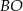 tego trójkąta.
tego trójkąta.
A) 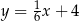 B)
B) 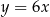 C)
C) 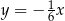 D)
D) 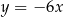
W układzie współrzędnych dany jest okrąg  opisany równaniem
opisany równaniem 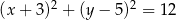 . Pole trójkąta równobocznego wpisanego w ten okrąg jest równe
. Pole trójkąta równobocznego wpisanego w ten okrąg jest równe
A) 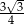 B) 6 C)
B) 6 C) 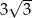 D)
D)