Ile jest wszystkich liczb naturalnych dwucyfrowych podzielnych przez 6 i niepodzielnych przez 9?
A) 6 B) 10 C) 12 D) 15
/Szkoła średnia/Zadania testowe/Kombinatoryka
Ile jest wszystkich liczb naturalnych dwucyfrowych podzielnych przez 14 i niepodzielnych przez 4?
A) 4 B) 6 C) 5 D) 7
Ile jest liczb naturalnych czterocyfrowych, których iloczyn cyfr jest liczbą pierwszą?
A) 17 B) 16 C) 24 D) 25
Ile jest liczb naturalnych pięciocyfrowych, których iloczyn cyfr jest liczbą pierwszą?
A) 20 B) 21 C) 16 D) 17
Ile jest liczb naturalnych sześciocyfrowych, których iloczyn cyfr jest liczbą pierwszą?
A) 20 B) 21 C) 24 D) 25
Ze zbioru 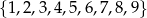 wybieramy jedną liczbę, a potem jeszcze jedną większą od niej. Na ile sposobów możemy to zrobić?
wybieramy jedną liczbę, a potem jeszcze jedną większą od niej. Na ile sposobów możemy to zrobić?
A) 72 B) 36 C) 81 D) 17
Ile jest liczb naturalnych pięciocyfrowych, których iloczyn cyfr jest dodatnią liczbą złożoną?
A) 59029 B) 59028 C) 89980 D) 89979
Na okręgu wybrano 20 punktów i połowę z nich pomalowano na biało, a drugą połowę na czarno. Ile jest odcinków o końcach w tych punktach, których jeden koniec jest biały, a drugi czarny?
A) 380 B) 190 C) 90 D) 100
Do pomieszczenia wchodzi grupa osób składająca się z 5 kobiet i 4 mężczyzn. Pierwsze wchodzą kobiety, a za nimi mężczyźni. Liczba wszystkich możliwych sposobów takiego wejścia osób do pomieszczenia jest równa
A) 9 B) 20 C) 2880 D) 144
Do fotografii rodzinnej ustawiają się rodzice, a przed nimi czwórka dzieci. Wszystkich możliwych ustawień jest
A) 6 B) 24 C) 26 D) 48
Do pomieszczenia wchodzi grupa osób składająca się z 5 dziewczynek i 5 chłopców. Pierwsze wchodzą dziewczynki, a za nimi chłopcy. Liczba wszystkich możliwych sposobów takiego wejścia osób do pomieszczenia jest równa
A) 25 B) 32 C) 240 D) 14400
Do pomieszczenia wchodzi grupa osób składająca się z 4 kobiet i 6 mężczyzn. Pierwsi wchodzą mężczyźni, a za nimi kobiety. Liczba wszystkich możliwych sposobów takiego wejścia osób do pomieszczenia jest równa
A) 17280 B) 4096 C) 2880 D) 144
Do fotografii rodzinnej ustawiają się rodzice, a przed nimi trójka dzieci. Wszystkich możliwych ustawień jest
A) 5 B) 6 C) 12 D) 144
Ile liczb o różnych cyfrach i większych od 6000 można utworzyć z cyfr 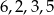 ?
?
A) 24 B) 18 C) 6 D) 30
Ile jest wszystkich liczb czterocyfrowych, większych 3200, utworzonych wyłącznie z cyfr 1, 2, 3, przy założeniu, że cyfry mogą się powtarzać, ale nie wszystkie z tych cyfr muszą być wykorzystane?
A) 9 B) 6 C) 18 D) 27
Ile jest wszystkich liczb czterocyfrowych, większych 3000, utworzonych wyłącznie z cyfr 1, 2, 3, przy założeniu, że cyfry mogą się powtarzać, ale nie wszystkie z tych cyfr muszą być wykorzystane?
A) 3 B) 6 C) 9 D) 27
Ania wyjeżdżając na wakacje zamknęła walizkę za pomocą kodu czterocyfrowego. Pamiętała, że druga liczba jest liczbą pierwszą mniejszą od 7, trzecia jest liczbą nieparzystą, a czwarta to 5, ale zapomniała pierwszej liczby. Ile maksymalnie prób musi wykonać, aby otworzyć walizkę?
A) 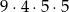 B)
B) 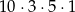 C)
C) 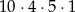 D)
D) 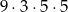
Wszystkich liczb naturalnych pięciocyfrowych, w których cyfrą jedności jest 4, cyfra setek jest liczba nieparzystą, a cyfra tysięcy jest liczbą podzielną przez 3 jest
A) 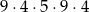 B)
B) 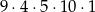 C)
C) 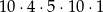 D)
D) 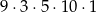
Na ile sposobów można wybrać dwóch graczy spośród 10 zawodników?
A) 100 B) 90 C) 45 D) 20
Na przyjęciu spotkało się jedenaście osób i każda osoba uścisnęła dłoń każdej innej osobie. Liczba wszystkich uścisków dłoni była równa
A) 21 B) 55 C) 121 D) 110
Każdy uczestnik spotkania dwunastoosobowej grupy przyjaciół uścisnął dłoń każdemu z pozostałych członków tej grupy. Liczba wszystkich uścisków dłoni była równa
A) 66 B) 72 C) 132 D) 144
Ile można utworzyć liczb czterocyfrowych podzielnych przez 20, o cyfrach należących do zbioru 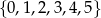 ?
?
A) 12 B) 60 C) 90 D) 20
Ile można utworzyć liczb pięciocyfrowych podzielnych przez 20, w których zapisie dziesiętnym nie występuje cyfra 7?
A) 3645 B) 2592 C) 3240 D) 2560
Ile można utworzyć liczb czterocyfrowych podzielnych przez 20, o cyfrach należących do zbioru 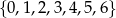 ?
?
A) 168 B) 196 C) 144 D) 126
Ile można utworzyć liczb trzycyfrowych podzielnych przez 5, o różnych cyfrach należących do zbioru 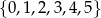 ?
?
A) 40 B) 36 C) 32 D) 28
Ile można utworzyć liczb trzycyfrowych podzielnych przez 5, o cyfrach należących do zbioru 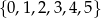 ?
?
A) 45 B) 36 C) 32 D) 28
Ile można utworzyć liczb trzycyfrowych podzielnych przez 5 większych od 199, o różnych cyfrach należących do zbioru 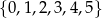 ?
?
A) 40 B) 36 C) 32 D) 28
Wszystkich różnych liczb naturalnych czterocyfrowych, w których zapisie dziesiętnym są dokładnie 3 takie same cyfry jest
A) 400 B) 360 C) 288 D) 324
Wszystkich liczb trzycyfrowych parzystych, których cyfra jedności należy do zbioru 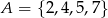 , cyfra dziesiątek do zbioru
, cyfra dziesiątek do zbioru 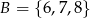 , a cyfra setek do zbioru
, a cyfra setek do zbioru 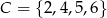 jest:
jest:
A) 48 B) 36 C) 24 D) 12
Wybieramy liczbę  ze zbioru
ze zbioru 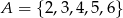 oraz liczbę
oraz liczbę 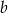 ze zbioru
ze zbioru 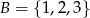 . Ile jest takich par
. Ile jest takich par 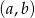 , że iloczyn
, że iloczyn 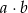 jest liczbą parzystą?
jest liczbą parzystą?
A) 11 B) 21 C) 5 D) 9
Wybieramy liczbę  ze zbioru
ze zbioru 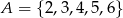 oraz liczbę
oraz liczbę 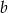 ze zbioru
ze zbioru 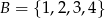 . Ile jest takich par
. Ile jest takich par 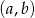 , że iloczyn
, że iloczyn 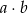 jest liczbą parzystą?
jest liczbą parzystą?
A) 11 B) 16 C) 20 D) 9
Kasia przygotowała 6 karteczek w ten sposób, że na każdej karteczce napisana jest jedna cyfra. Ile różnych liczb 6 cyfrowych można utworzyć kładąc obok siebie te karteczki, jeżeli na karteczkach napisane są cyfry: 1, 1, 2, 3, 4, 5?
A) 120 B) 320 C) 360 D) 720
W karcie dań jest 5 zup i 4 drugie dania. Na ile sposobów można zamówić obiad składający się z jednej zupy i jednego drugiego dania?
A) 25 B) 20 C) 16 D) 9
W karcie dań są 4 zupy i 6 drugich dań. Na ile sposobów można zamówić obiad składający się z jednej zupy i jednego drugiego dania?
A) 24 B) 10 C) 16 D) 30
Liczba sześcianów liczb całkowitych w zbiorze kolejnych liczb naturalnych
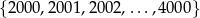
jest równa
A) 3 B) 4 C) 5 D) 8
Liczba sześcianów liczb całkowitych w zbiorze kolejnych liczb naturalnych
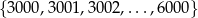
jest równa
A) 3 B) 4 C) 5 D) 8
Wyrażenie 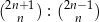 dla liczby naturalnej
dla liczby naturalnej 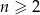 jest równe
jest równe
A) 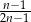 B)
B) 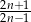 C) 2 D)
C) 2 D) 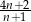
Liczba punktów, których pierwsza współrzędna należy do zbiory 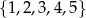 , a druga do zbioru
, a druga do zbioru 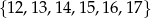 jest równa
jest równa
A) 11 B) 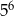 C)
C) 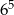 D) 30
D) 30
Liczba punktów, których pierwsza współrzędna należy do zbiory 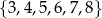 , a druga do zbioru
, a druga do zbioru 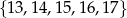 jest równa
jest równa
A) 30 B) 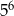 C)
C) 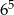 D) 11
D) 11
W turnieju szachowym rozegrano 36 partii. Każdy zawodnik rozegrał z każdym dokładnie 1 mecz. Ilu zawodników brało udział w turnieju?
A) 10 B) 9 C) 8 D) 7
W turnieju szachowym rozegrano 28 partii. Każdy zawodnik rozegrał z każdym dokładnie 1 mecz. Ilu zawodników brało udział w turnieju?
A) 10 B) 9 C) 8 D) 7
W turnieju szachowym rozegrano 45 partii. Każdy zawodnik rozegrał z każdym dokładnie 1 mecz. Ilu zawodników brało udział w turnieju?
A) 10 B) 9 C) 8 D) 7

