Wszystkich liczb naturalnych trzycyfrowych parzystych, w których cyfra 7 występuje dokładnie jeden raz, jest
A) 85 B) 90 C) 100 D) 150
/Szkoła średnia/Zadania testowe/Kombinatoryka
Ile jest wszystkich czterocyfrowych liczb naturalnych podzielnych przez 3?
A) 3000 B) 3333 C) 2999 D) 2998
Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2020 i podzielnych przez 4?
A) 506 B) 505 C) 256 D) 255
Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2019 i podzielnych przez 4?
A) 256 B) 257 C) 255 D) 128
Ile jest wszystkich czterocyfrowych liczb naturalnych podzielnych przez 13?
A) 692 B) 691 C) 690 D) 693
Ile jest wszystkich czterocyfrowych liczb naturalnych podzielnych przez 7?
A) 1285 B) 1428 C) 1284 D) 1286
Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2021 i podzielnych przez 3?
A) 673 B) 334 C) 340 D) 339
Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2018 i podzielnych przez 5?
A) 402 B) 403 C) 203 D) 204
Ile jest wszystkich liczb naturalnych czterocyfrowych podzielnych przez 5?
A) 2000 B) 1800 C) 1000 D) 900
Ile jest wszystkich liczb naturalnych trzycyfrowych podzielnych przez 5?
A) 90 B) 100 C) 180 D) 200
Ile jest wszystkich pięciocyfrowych liczb naturalnych podzielnych przez 29?
A) 3103 B) 3105 C) 3104 D) 3106
Ile jest wszystkich liczb naturalnych dodatnich mniejszych od 2021, których cyfra jedności jest jedną z cyfr: 0, 2, 6, 8?
A) 1010 B) 808 C) 606 D) 560
W pudełku znajduje się 5 kartek, na których zapisano wszystkie możliwe jednocyfrowe liczby naturalne nieparzyste. Wyjmujemy z pudełka kolejno trzy kartki i układając je jedna obok drugiej tworzymy liczby trzycyfrowe. Liczb takich możemy utworzyć maksymalnie
A) 120 B) 125 C) 60 D) 15
W pudełku znajduje się 5 kartek, na których zapisano liczby: 0, 2, 4, 6, 8. Wyjmujemy z pudełka kolejno trzy kartki i układając je jedna obok drugiej tworzymy liczby trzycyfrowe. Liczb takich możemy utworzyć maksymalnie
A) 48 B) 125 C) 100 D) 60
Wszystkich liczb naturalnych czterocyfrowych parzystych, w których cyfra 5 występuje dokładnie jeden raz, jest
A) 3285 B) 1125 C) 765 D) 3240
Ile jest wszystkich liczb naturalnych mniejszych od 500 utworzonych z cyfr: 1, 3, 5, 7, 9 (cyfry mogą się powtarzać)?
A) 125 B) 80 C) 75 D) 50
W kolejce do kasy biletowej ustawiły się cztery dziewczynki i pięciu chłopców. Liczba wszystkich możliwych ustawień osób w tej kolejce wynosi
A) 4!+5! B) 9! C) 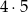 D)
D) 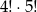
W kolejce do kasy kinowej ustawiło się sześciu mężczyzn i trzy kobiety. Liczba wszystkich możliwych ustawień osób w tej kolejce wynosi
A) 6!+3! B) 9! C) 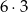 D)
D) 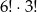
Na ile sposobów można ustawić na półce 5 tomów encyklopedii tak, aby tomy 3 i 4 stały obok siebie (w dowolnej kolejności)?
A) 24 B) 48 C) 120 D) 60
Na ile sposobów można ustawić na półce 6 tomów encyklopedii tak, aby tomy 4, 5 i 6 stały obok siebie (w dowolnej kolejności)?
A) 144 B) 48 C) 72 D) 24
Ze zbioru 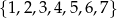 wybieramy kolejno cztery liczby bez zwracania i układamy je w kolejności losowania w liczbę czterocyfrową. Liczb czterocyfrowych podzielnych przez 5 otrzymamy:
wybieramy kolejno cztery liczby bez zwracania i układamy je w kolejności losowania w liczbę czterocyfrową. Liczb czterocyfrowych podzielnych przez 5 otrzymamy:
A) 216 B) 120 C) 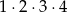 D)
D) 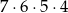
Wszystkich różnych liczb naturalnych czterocyfrowych, które są nieparzyste i podzielne przez 25, jest
A) 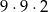 B)
B) 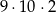 C)
C) 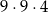 D)
D) 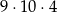
Wszystkich różnych liczb naturalnych czterocyfrowych, które są parzyste i podzielne przez 25, jest
A) 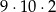 B)
B) 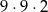 C)
C) 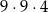 D)
D) 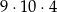
Liczb naturalnych sześciocyfrowych podzielnych przez 5, których cyfra setek należy do zbioru 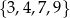 i wszystkie cyfry są różne jest
i wszystkie cyfry są różne jest
A) 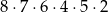 B)
B) 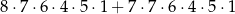
C) 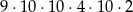 D)
D) 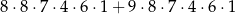
Wszystkich różnych liczb naturalnych czterocyfrowych nieparzystych podzielnych przez 5 jest
A) 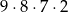 B)
B) 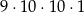 C)
C) 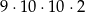 D)
D) 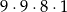
Liczb naturalnych trzycyfrowych, w zapisie których każda cyfra występuje co najwyżej raz oraz suma cyfry setek i cyfry jedności jest równa 4, jest
A) mniej niż 24 B) dokładnie 24 C) dokładnie 32 D) więcej niż 32
Liczby 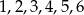 ustawiamy losowo w ciąg. Wszystkich możliwych ustawień takich, że liczby 1 i 6 sąsiadują ze sobą (w dowolnej kolejności), jest
ustawiamy losowo w ciąg. Wszystkich możliwych ustawień takich, że liczby 1 i 6 sąsiadują ze sobą (w dowolnej kolejności), jest
A) 10 B) 12 C) 48 D) 240
Liczby 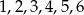 ustawiamy losowo w ciąg. Wszystkich możliwych ustawień takich, że liczby 1, 3 i 6 sąsiadują ze sobą (w dowolnej kolejności), jest
ustawiamy losowo w ciąg. Wszystkich możliwych ustawień takich, że liczby 1, 3 i 6 sąsiadują ze sobą (w dowolnej kolejności), jest
A) 72 B) 40 C) 192 D) 144
Liczby 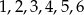 ustawiamy losowo w ciąg. Wszystkich możliwych ustawień takich, że liczby 1 i 6 są oddzielone od siebie dokładnie jedną cyfrą (w dowolnej kolejności), jest
ustawiamy losowo w ciąg. Wszystkich możliwych ustawień takich, że liczby 1 i 6 są oddzielone od siebie dokładnie jedną cyfrą (w dowolnej kolejności), jest
A) 8 B) 192 C) 48 D) 240
Wybieramy jedną liczbę ze zbioru 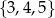 i jedną liczbę ze zbioru
i jedną liczbę ze zbioru 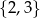 . Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
. Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
A) 3 B) 4 C) 5 D) 6
Wybieramy jedną liczbę ze zbioru 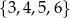 i jedną liczbę ze zbioru
i jedną liczbę ze zbioru 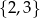 . Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą parzystą?
. Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą parzystą?
A) 3 B) 4 C) 5 D) 6
Wybieramy jedną liczbę ze zbioru 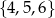 i jedną liczbę ze zbioru
i jedną liczbę ze zbioru 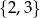 . Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
. Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
A) 6 B) 5 C) 4 D) 3
Na ile sposobów można włożyć dwie skarpetki do czterech szuflad?
A) 16 B) 8 C) 256 D) 32
Na ile sposobów można włożyć trzy skarpetki do czterech różnych szuflad?
A) 12 B) 81 C) 256 D) 64
Na ile sposobów można włożyć dwie czapki do pięciu różnych szuflad?
A) 10 B) 25 C) 64 D) 32
Wszystkich liczb naturalnych trzycyfrowych, większych od 700, w których każda cyfra należy do zbioru 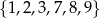 i żadna cyfra się nie powtarza, jest
i żadna cyfra się nie powtarza, jest
A) 108 B) 60 C) 40 D) 299
Wszystkich liczb naturalnych trzycyfrowych, mniejszych od 600, w których każda cyfra należy do zbioru 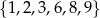 i żadna cyfra się nie powtarza, jest
i żadna cyfra się nie powtarza, jest
A) 108 B) 60 C) 40 D) 299
Wybieramy liczbę  ze zbioru
ze zbioru 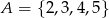 oraz liczbę
oraz liczbę 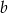 ze zbioru
ze zbioru 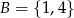 . Ile jest takich par
. Ile jest takich par 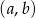 , że iloczyn
, że iloczyn 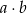 jest liczbą nieparzystą?
jest liczbą nieparzystą?
A) 2 B) 3 C) 5 D) 20
Wybieramy liczbę  ze zbioru
ze zbioru 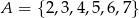 oraz liczbę
oraz liczbę 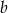 ze zbioru
ze zbioru 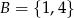 . Ile jest takich par
. Ile jest takich par 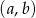 , że iloczyn
, że iloczyn 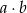 jest liczbą nieparzystą?
jest liczbą nieparzystą?
A) 2 B) 3 C) 5 D) 20
Wybieramy liczbę  ze zbioru
ze zbioru 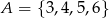 oraz liczbę
oraz liczbę 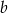 ze zbioru
ze zbioru 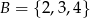 . Ile jest takich par
. Ile jest takich par 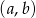 , że iloczyn
, że iloczyn 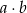 jest liczbą nieparzystą?
jest liczbą nieparzystą?
A) 12 B) 3 C) 2 D) 20
Wybieramy liczbę  ze zbioru
ze zbioru 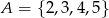 oraz liczbę
oraz liczbę 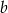 ze zbioru
ze zbioru 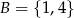 . Ile jest takich par
. Ile jest takich par 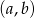 , że iloczyn
, że iloczyn 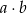 jest liczbą parzystą?
jest liczbą parzystą?
A) 2 B) 8 C) 6 D) 20
Każdy bok trójkąta prostokątnego o bokach 3, 4, 5 kolorujemy jednym z 6 kolorów tak, aby żadne dwa boki nie były pokolorowane tym samym kolorem. Ile jest takich pokolorowań?
A) 15 B) 120 C) 216 D) 20
Wszystkie ściany sześcianu pomalowano. Następnie sześcian rozcięto na 64 jednakowe sześcianiki. Ile sześcianików ma pomalowaną co najmniej jedną ścianę?
A) 37 B) 56 C) 60 D) 63
Wszystkie ściany sześcianu pomalowano. Następnie sześcian rozcięto na 64 jednakowe sześcianiki. Ile sześcianików ma pomalowaną co najwyżej jedną ścianę.?
A) 48 B) 56 C) 40 D) 32
Wszystkie ściany sześcianu pomalowano. Następnie sześcian rozcięto na 64 jednakowe sześcianiki. Ile sześcianików ma pomalowaną co najmniej dwie ściany?
A) 32 B) 72 C) 56 D) 40
Trzech panów i  pań można ustawić w jednym rzędzie na 12 sposobów, tak aby osoby tej samej płci nie stały obok siebie. Liczba
pań można ustawić w jednym rzędzie na 12 sposobów, tak aby osoby tej samej płci nie stały obok siebie. Liczba  pań jest równa
pań jest równa
A) 8 B) 4 C) 5 D) 2
Trzech panów i  pań można ustawić w jednym rzędzie na 144 sposoby, tak aby osoby tej samej płci nie stały obok siebie. Liczba
pań można ustawić w jednym rzędzie na 144 sposoby, tak aby osoby tej samej płci nie stały obok siebie. Liczba  pań jest równa
pań jest równa
A) 8 B) 4 C) 3 D) 2
Na regale można ustawić  książek na 24 sposoby. Zatem
książek na 24 sposoby. Zatem
A) 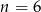 B)
B) 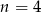 C)
C) 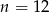 D)
D) 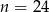
Na regale można ustawić  książek na 120 sposoby. Zatem
książek na 120 sposoby. Zatem
A) 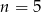 B)
B) 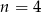 C)
C) 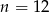 D)
D) 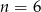
W kolejce do sklepu  osób można ustawić na 24 sposoby. Zatem
osób można ustawić na 24 sposoby. Zatem
A) 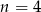 B)
B) 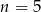 C)
C) 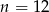 D)
D) 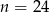
Ile jest liczb naturalnych dwudziestocyfrowych, których iloczyn cyfr jest równy 25?
A) 380 B) 190 C) 250 D) 500

