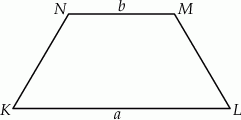
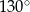Dany jest trapez równoramienny 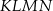 , którego podstawy mają długości
, którego podstawy mają długości 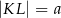 ,
, 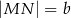 ,
, 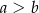 . Kąt
. Kąt 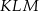 ma miarę
ma miarę 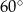 . Długość ramienia
. Długość ramienia 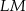 tego trapezu jest równa
tego trapezu jest równa
A) 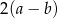 B)
B) 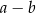 C)
C) 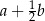 D)
D) 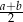
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest trapez równoramienny 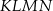 , którego podstawy mają długości
, którego podstawy mają długości 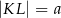 ,
, 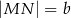 ,
, 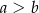 . Kąt
. Kąt 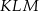 ma miarę
ma miarę 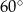 . Długość ramienia
. Długość ramienia 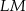 tego trapezu jest równa
tego trapezu jest równa

A) 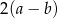 B)
B) 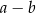 C)
C) 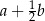 D)
D) 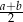
W trapezie równoramiennym 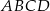 podstawy
podstawy 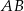 i
i 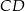 mają długości równe odpowiednio
mają długości równe odpowiednio  i
i 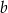 (przy czym
(przy czym 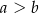 ). Miara kąta ostrego trapezu jest równa
). Miara kąta ostrego trapezu jest równa 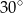 . Wtedy wysokość tego trapezu jest równa
. Wtedy wysokość tego trapezu jest równa
A) 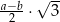 B)
B) 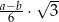 C)
C) 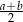 D)
D) 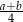
Trapez 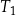 , o polu równym 52 i obwodzie 36, jest podobny do trapezu
, o polu równym 52 i obwodzie 36, jest podobny do trapezu 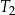 . Pole trapezu
. Pole trapezu 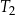 jest równe 13. Obwód trapezu
jest równe 13. Obwód trapezu 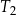 jest równy
jest równy
A) 18 B) 9 C) 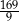 D)
D) 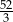
Miary dwóch kątów trapezu równoramiennego pozostają w stosunku 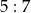 . Wynika stąd, że największy kąt tego trapezu ma miarę
. Wynika stąd, że największy kąt tego trapezu ma miarę
A) 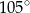 B)
B) 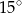 C)
C) 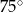 D)
D) 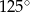
W trapezie 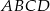 (
(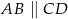 ) dłuższa podstawa ma długość
) dłuższa podstawa ma długość 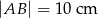 . Odcinek łączący środki ramion w tym trapezie ma długość 7 cm. Długość krótszej podstawy wynosi
. Odcinek łączący środki ramion w tym trapezie ma długość 7 cm. Długość krótszej podstawy wynosi
A) 5 cm B) 7 cm C) 4 cm D) 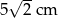
W trapezie 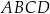 o podstawach
o podstawach 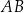 i
i 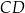 przekątne przecinają się w punkcie
przekątne przecinają się w punkcie 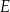 (zobacz rysunek).
(zobacz rysunek).
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt  jest podobny do trójkąta jest podobny do trójkąta  . . | P | F |
Pole trójkąta 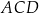 jest równe polu trójkąta jest równe polu trójkąta 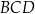 . . | P | F |
W trapezie 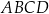 podstawa
podstawa 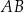 jest dłuższa od podstawy
jest dłuższa od podstawy 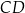 . Przekątne trapezu przecinają się w punkcie
. Przekątne trapezu przecinają się w punkcie 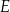 (zobacz rysunek).
(zobacz rysunek).
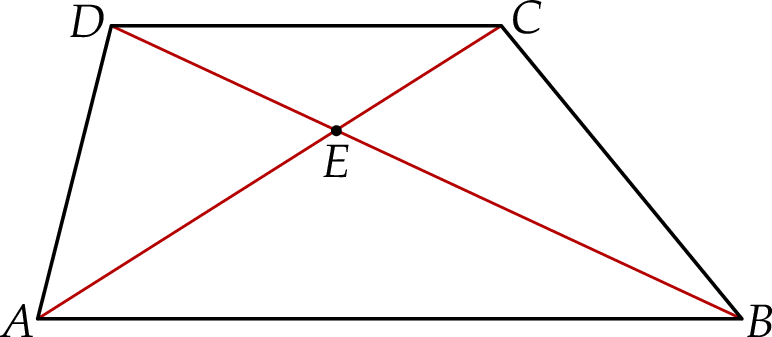
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 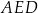 jest równe polu trójkąta jest równe polu trójkąta 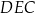 . . | P | F |
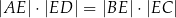 | P | F |
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 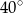 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 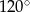 B)
B) 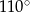 C)
C) 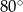 D)
D) 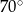
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 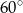 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 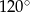 B)
B) 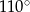 C)
C) 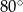 D)
D) 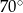
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 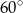 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 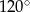 B)
B) 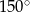 C)
C) 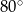 D)
D) 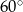
Różnica miar dwóch kątów rozwartych trapezu jest równa 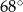 . Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
. Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
A) 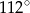 B)
B) 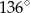 C)
C) 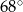 D)
D) 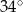
W trapezie prostokątnym kąt ostry ma miarę 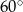 . Wysokość tego trapezu jest równa 3 cm. O ile centymetrów dłuższa jest jedna podstawa od drugiej?
. Wysokość tego trapezu jest równa 3 cm. O ile centymetrów dłuższa jest jedna podstawa od drugiej?
A) 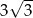 B) 6 C) 3 D)
B) 6 C) 3 D) 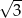
Przekątne trapezu 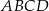 , w którym
, w którym 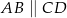 przecinają się w punkcie
przecinają się w punkcie 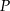 w ten sposób, że
w ten sposób, że 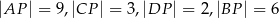 oraz
oraz 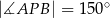 . Pole tego trapezu jest równe
. Pole tego trapezu jest równe
A) 32 B) 24 C) 18 D) 16
Dany jest trapez 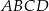 , w którym
, w którym 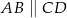 oraz przekątne
oraz przekątne 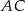 i
i 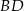 przecinają się w punkcie
przecinają się w punkcie 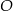 . Wysokość tego trapezu jest równa 12. Obwód trójkąta
. Wysokość tego trapezu jest równa 12. Obwód trójkąta 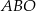 jest równy 39, a obwód trójkąta
jest równy 39, a obwód trójkąta 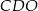 jest równy 13.
jest równy 13.
Wysokość trójkąta  poprowadzona z punktu
poprowadzona z punktu  jest równa
jest równa
A) 3 B) 4 C) 9 D) 6
Dany jest trapez 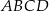 , w którym
, w którym 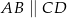 oraz przekątne
oraz przekątne 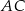 i
i 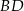 przecinają się w punkcie
przecinają się w punkcie 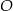 . Wysokość tego trapezu jest równa 15. Obwód trójkąta
. Wysokość tego trapezu jest równa 15. Obwód trójkąta 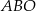 jest równy 42, a obwód trójkąta
jest równy 42, a obwód trójkąta 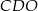 jest równy 14.
jest równy 14.
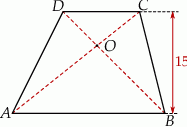
Wysokość trójkąta 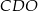 poprowadzona z punktu
poprowadzona z punktu 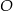 jest równa
jest równa
A) 3,75 B) 5 C) 6 D) 7,5
Długości podstaw trapezu wynoszą  oraz
oraz 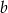 , gdzie
, gdzie 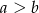 . Zatem odcinek, którego końcami są środki ramion trapezu, ma długość
. Zatem odcinek, którego końcami są środki ramion trapezu, ma długość
A) 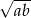 B)
B) 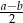 C)
C) 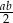 D)
D) 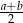
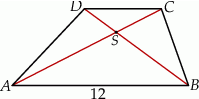
Przekątne trapezu 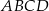 przecinają się w punkcie
przecinają się w punkcie  w ten sposób, że pole trójkąta
w ten sposób, że pole trójkąta 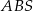 jest 4 razy większe od pola trójkąta
jest 4 razy większe od pola trójkąta 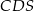 .
.
Jeżeli podstawa 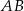 ma długość 12, to długość podstawy
ma długość 12, to długość podstawy 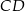 jest równa
jest równa
A) 8 B) 3 C) 6 D) 9
Z odcinków o długościach: 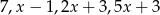 można zbudować trapez równoramienny. Wynika stąd, że
można zbudować trapez równoramienny. Wynika stąd, że
A) 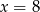 B)
B) 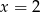 C)
C)  D)
D) 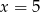
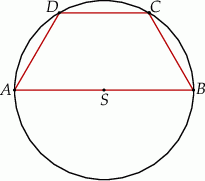
W okręgu o promieniu 6 poprowadzono cięciwę 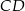 równoległą do średnicy
równoległą do średnicy 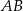 tego okręgu i taką, że
tego okręgu i taką, że 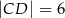 (zobacz rysunek).
(zobacz rysunek).
Obwód trapezu 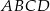 jest równy
jest równy
A) 30 B) 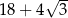 C)
C) 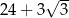 D) 32
D) 32
Długości boków trapezu równoramiennego są równe 12, 13, 2, 13.
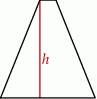
Wysokość 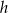 tego trapezu jest równa
tego trapezu jest równa
A) 5 B) 8 C) 10 D) 12
Długości boków trapezu równoramiennego są równe 19, 17, 3, 17.
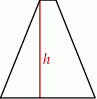
Wysokość 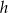 tego trapezu jest równa
tego trapezu jest równa
A) 16 B) 15 C) 14 D) 13
W trapezie  , w którym
, w którym 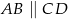 , przedłużono ramiona
, przedłużono ramiona 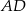 i
i 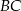 do przecięcia się w punkcie
do przecięcia się w punkcie 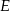 . Wiadomo, że
. Wiadomo, że 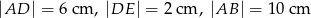 . Wobec tego odcinek
. Wobec tego odcinek 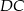 ma długość
ma długość
A) 2,5 cm B) 2 cm C) 3 cm D) 3,5 cm
W trapezie 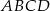 , w którym
, w którym 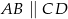 , przedłużono ramiona
, przedłużono ramiona 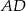 i
i 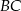 do przecięcia się w punkcie
do przecięcia się w punkcie 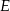 . Wiadomo, że
. Wiadomo, że 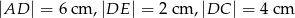 . Wobec tego odcinek
. Wobec tego odcinek 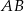 ma długość
ma długość
A) 15,5 cm B) 15 cm C) 16 cm D) 16,5 cm
W trapezie 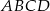 , w którym
, w którym 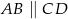 , przedłużono ramiona
, przedłużono ramiona 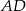 i
i 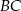 do przecięcia się w punkcie
do przecięcia się w punkcie 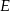 . Wiadomo, że
. Wiadomo, że 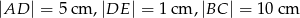 . Wobec tego odcinek
. Wobec tego odcinek 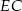 ma długość
ma długość
A) 2,5 cm B) 2 cm C) 3 cm D) 3,5 cm
Dany jest trapez 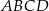 , w którym
, w którym 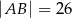 ,
, 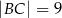 ,
, 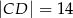 i
i 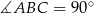 (zobacz rysunek).
(zobacz rysunek).
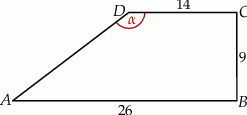
Stąd wynika, że cosinus zaznaczonego na rysunku kąta  jet równy
jet równy
A)  B)
B) 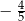 C)
C) 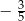 D)
D) 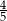
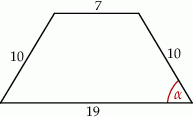
Dany jest trapez równoramienny (patrz rysunek). Wtedy 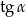 jest równy
jest równy
A) 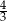 B)
B)  C)
C)  D)
D) 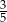
Dany jest trapez równoramienny (patrz rysunek). Wtedy 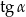 jest równy
jest równy
A) 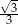 B)
B) 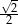 C)
C) 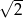 D)
D) 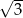
Dany jest trapez prostokątny 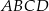 , w którym
, w którym 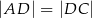 oraz
oraz 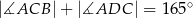 (zobacz rysunek).
(zobacz rysunek).
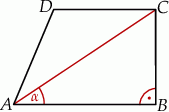
Stąd wynika, że
A) 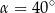 B)
B) 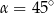 C)
C) 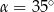 D)
D) 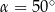
Punkty 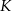 i
i 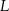 są punktami styczności okręgu wpisanego w trapez równoramienny
są punktami styczności okręgu wpisanego w trapez równoramienny 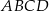 z bokami
z bokami 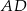 i
i 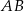 . Kąt ostry tego trapezu ma miarę
. Kąt ostry tego trapezu ma miarę 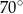 (zobacz rysunek).
(zobacz rysunek).
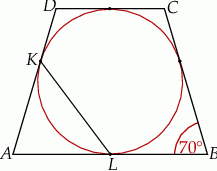
Miara kąta 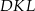 jest równa
jest równa
A) 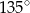 B)
B) 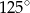 C)
C) 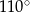 D)
D)