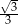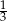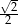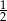Na rysunku przedstawiono okrąg o środku 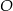 , który jest styczny do wszystkich boków trapezu równoramiennego
, który jest styczny do wszystkich boków trapezu równoramiennego 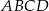 . Ramiona
. Ramiona 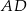 i
i 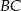 są styczne do tego okręgu odpowiednio w punktach
są styczne do tego okręgu odpowiednio w punktach 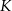 i
i 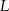 . Kąt wypukły
. Kąt wypukły 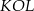 ma miarę
ma miarę 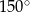 .
.
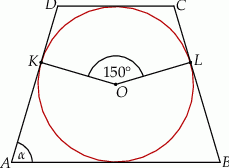
Miara  kąta ostrego tego trapezu jest równa
kąta ostrego tego trapezu jest równa
A) 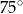 B)
B) 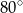 C)
C) 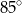 D)
D) 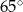

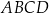 , w którym przekątna
, w którym przekątna 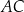 jest prostopadła do ramienia
jest prostopadła do ramienia 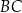 ,
, 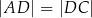 oraz
oraz 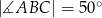 (zobacz rysunek).
(zobacz rysunek). 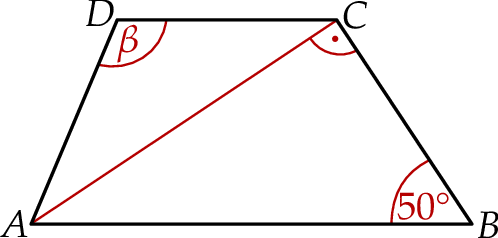
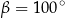
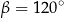
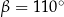
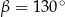
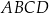 , w którym bok
, w którym bok 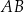 jest równoległy do boku
jest równoległy do boku 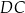 . W tym trapezie poprowadzono odcinek
. W tym trapezie poprowadzono odcinek 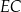 równoległy do boku
równoległy do boku 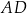 , podano miary dwóch kątów oraz oznaczono kąt
, podano miary dwóch kątów oraz oznaczono kąt  (zobacz rysunek).
(zobacz rysunek). 
 ma miarę
ma miarę 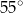
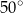
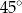
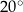
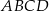 , w którym przekątna
, w którym przekątna 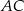 jest prostopadła do ramienia
jest prostopadła do ramienia 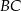 ,
, 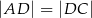 oraz
oraz 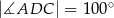 (zobacz rysunek).
(zobacz rysunek). 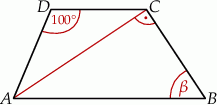
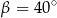
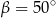
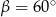
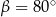
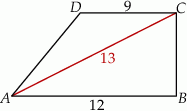
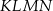 , którego podstawy mają długości
, którego podstawy mają długości 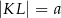 ,
, 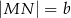 ,
, 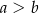 . Kąt
. Kąt 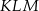 ma miarę
ma miarę 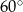 . Długość ramienia
. Długość ramienia 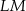 tego trapezu jest równa
tego trapezu jest równa 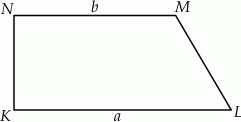
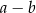
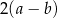
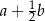
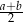
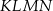 , którego podstawy mają długości
, którego podstawy mają długości 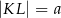 ,
, 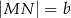 ,
, 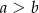 . Kąt
. Kąt 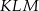 ma miarę
ma miarę 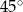 . Długość ramienia
. Długość ramienia 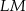 tego trapezu jest równa
tego trapezu jest równa 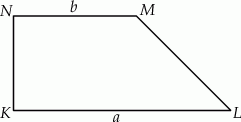
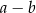
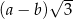
 podzielono przekątną
podzielono przekątną 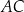 na dwa trójkąty. Punkty
na dwa trójkąty. Punkty 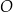 i
i 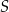 są środkami okręgów wpisanych w trójkąty
są środkami okręgów wpisanych w trójkąty 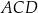 i
i 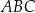 , a odcinek
, a odcinek 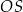 przecina przekątną
przecina przekątną 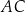 w punkcie
w punkcie 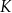 (zobacz rysunek). Stosunek długości okręgów o środkach
(zobacz rysunek). Stosunek długości okręgów o środkach 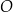 i
i 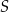 jest równy
jest równy  , a odcinek
, a odcinek 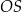 ma długość 24.
ma długość 24. 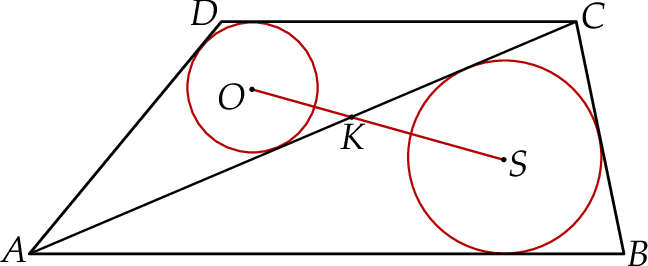
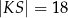
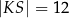
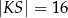
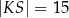
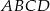 (
(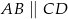 ) wysokość
) wysokość 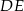 podzieliła podstawę na odcinki długości
podzieliła podstawę na odcinki długości 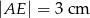 i
i 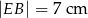 . Odcinek łączący środki ramion w tym trapezie ma długość
. Odcinek łączący środki ramion w tym trapezie ma długość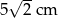
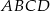 (
(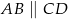 ) wysokość
) wysokość 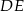 podzieliła podstawę na odcinki długości
podzieliła podstawę na odcinki długości 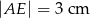 i
i 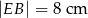 . Odcinek łączący środki ramion w tym trapezie ma długość
. Odcinek łączący środki ramion w tym trapezie ma długość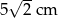
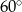 i ramieniu długości
i ramieniu długości 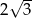 jest równa
jest równa 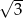
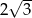
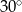 i ramieniu długości
i ramieniu długości 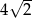 jest równa
jest równa 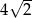
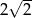
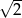
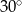 i ramieniu długości
i ramieniu długości 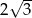 jest równa
jest równa 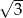
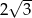
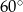 i ramieniu długości 12 może być równa
i ramieniu długości 12 może być równa 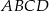 o podstawach
o podstawach 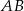 i
i 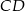 . Przedłużenia ramion przecinają się w punkcie
. Przedłużenia ramion przecinają się w punkcie 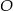 . Jeśli
. Jeśli 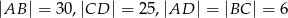 , to
, to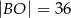
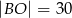
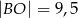
 . Przedłużenia ramion przecinają się w punkcie
. Przedłużenia ramion przecinają się w punkcie 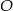 . Jeśli
. Jeśli 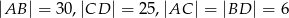 , to
, to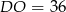
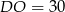
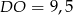
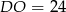
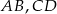 . Przedłużenia ramion przecinają się w punkcie
. Przedłużenia ramion przecinają się w punkcie 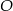 . Jeśli
. Jeśli 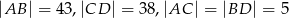 , to
, to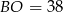
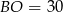
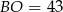
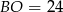
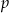 , zaś krótsza podstawa długość
, zaś krótsza podstawa długość  . Wobec tego
. Wobec tego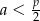
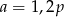
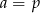
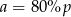
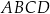 mają długości:
mają długości: 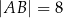 oraz
oraz 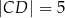 . Wysokość
. Wysokość 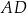 tego trapezu ma długość
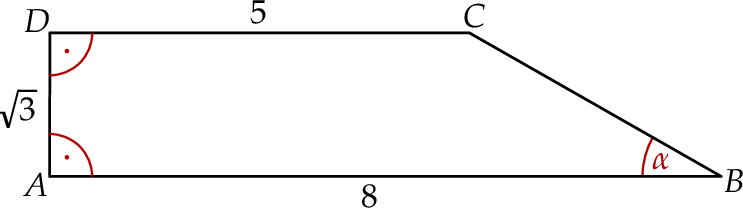
tego trapezu ma długość 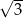 .
. 
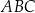 jest równa
jest równa 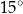
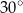
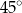
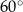
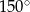
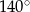
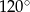
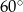
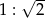 . Miara kąta rozwartego tego trapezu jest równa
. Miara kąta rozwartego tego trapezu jest równa 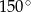
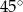
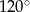
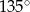
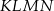 , w którym
, w którym 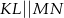 , kąt
, kąt 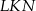 jest prosty (zobacz rysunek) oraz dane są:
jest prosty (zobacz rysunek) oraz dane są: 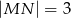 ,
, 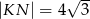 ,
, 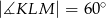 . Pole tego trapezu jest równe:
. Pole tego trapezu jest równe: 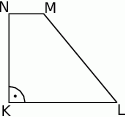
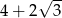
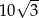
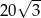
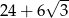
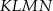 , w którym
, w którym 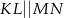 , kąt
, kąt 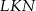 jest prosty (zobacz rysunek) oraz dane są:
jest prosty (zobacz rysunek) oraz dane są: 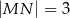 ,
, 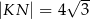 ,
, 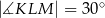 . Pole tego trapezu jest równe:
. Pole tego trapezu jest równe: 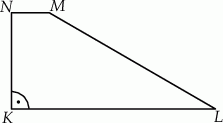

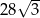
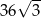
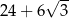
 przedstawionego na rysunku, jest równe
przedstawionego na rysunku, jest równe 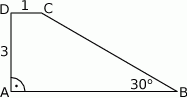
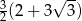
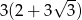
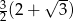
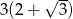
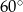 , a podstawy mają długości 12 i 6. Wysokość tego trapezu jest równa
, a podstawy mają długości 12 i 6. Wysokość tego trapezu jest równa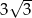
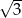

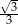
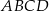 o podstawach
o podstawach 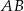 i
i 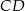 , w którym
, w którym 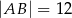 i
i 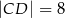 .
. 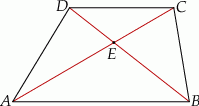
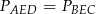
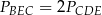
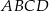 mają długości 8 i 16, a przekątne tego trapezu mają długość 15 (zobacz rysunek).
mają długości 8 i 16, a przekątne tego trapezu mają długość 15 (zobacz rysunek). 
 kąta ostrego
kąta ostrego 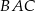 tego trójkąta spełnia warunek
tego trójkąta spełnia warunek 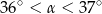
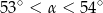
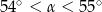
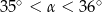
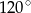 . Obwód trapezu jest równy
. Obwód trapezu jest równy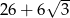
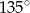 . Obwód trapezu jest równy
. Obwód trapezu jest równy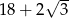
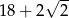
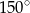 . Obwód trapezu jest równy
. Obwód trapezu jest równy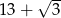
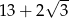
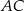 trapezu równoramiennego
trapezu równoramiennego 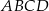 jest prostopadła do ramienia
jest prostopadła do ramienia 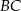 oraz tworzy z ramieniem
oraz tworzy z ramieniem 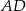 kąt ostry
kąt ostry  . Wysokość trapezu opuszczona z wierzchołka
. Wysokość trapezu opuszczona z wierzchołka 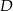 i ramię
i ramię 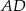 przecinają się pod kątem ostrym
przecinają się pod kątem ostrym 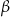 o mierze
o mierze 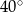 (zobacz rysunek).
(zobacz rysunek). 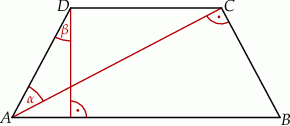
 ma miarę
ma miarę 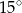
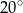
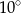
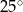
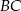 trapezu prostokątnego jest dwa razy większa od różnicy długości jego podstaw. Kąt
trapezu prostokątnego jest dwa razy większa od różnicy długości jego podstaw. Kąt 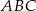 ma miarę
ma miarę 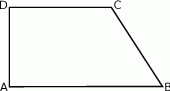
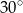
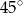
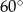
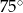
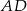 trapezu prostokątnego jest równa różnicy długości jego podstaw. Kąt
trapezu prostokątnego jest równa różnicy długości jego podstaw. Kąt 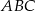 ma miarę
ma miarę 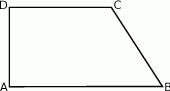
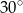
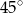
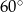
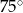
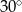 i
i 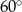 . Wówczas stosunek długości krótszego ramienia do dłuższego jest równy:
. Wówczas stosunek długości krótszego ramienia do dłuższego jest równy: