Oblicz pole trójkąta ograniczonego prostą 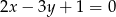 i osiami układu współrzędnych.
i osiami układu współrzędnych.
/Szkoła średnia
Wyznacz równanie okręgu symetrycznego do okręgu 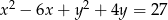 względem prostej
względem prostej 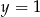 .
.
Cenę nart obniżono latem o 20%, a potem jeszcze o 15%. Po tych dwóch obniżkach narty kosztowały 705 zł i 50 gr. Wynika z tego, że pierwotna cena nart to
A) 952,42 zł B) 980 zł C) 1037,5 zł D) 1100 zł
Cenę aparatu fotograficznego obniżono o 15%, a następnie – o 20% w odniesieniu do ceny obowiązującej w danym momencie. Po tych dwóch obniżkach aparat kosztuje 340 zł. Przed obiema obniżkami cena tego aparatu była równa
A) 500 zł B) 425 zł C) 400 zł D) 375 zł
Cenę płetw obniżono zimą o 14%, a potem jeszcze o 20%. Po tych dwóch obniżkach płetwy kosztowały 242 zł i 52 gr. Wynika z tego, że pierwotna cena płetw to
A) 331,77 zł B) 352,5 zł C) 347 zł D) 395 zł
Cenę pontonu obniżono zimą o 15%, a potem jeszcze o 25%. Po tych dwóch obniżkach ponton kosztował 1912 zł i 50 gr. Wynika z tego, że pierwotna cena pontonu to
A) 3000 zł B) 2749,22 zł C) 2974,22 zł D) 2000 zł
Punkty 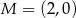 i
i 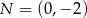 są punktami styczności okręgu z osiami układu współrzędnych. Jakie współrzędne ma środek tego okręgu?
są punktami styczności okręgu z osiami układu współrzędnych. Jakie współrzędne ma środek tego okręgu?
A) 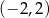 B)
B) 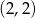 C)
C) 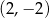 D)
D) 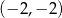
Punkty 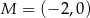 i
i 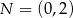 są punktami styczności okręgu z osiami układu współrzędnych. Jakie współrzędne ma środek tego okręgu?
są punktami styczności okręgu z osiami układu współrzędnych. Jakie współrzędne ma środek tego okręgu?
A) 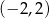 B)
B) 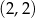 C)
C) 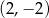 D)
D) 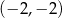
Podaj przykład liczb całkowitych dodatnich, spełniających nierówność 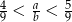 .
.
Podaj przykład liczb całkowitych 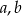 , dla których prawdziwa jest nierówność podwójna:
, dla których prawdziwa jest nierówność podwójna:
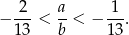
Podaj przykład liczb całkowitych dodatnich, spełniających nierówność 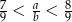 .
.
Podaj przykład liczb całkowitych dodatnich  i
i 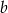 , spełniających nierówność
, spełniających nierówność 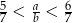 .
.
Dana jest funkcja 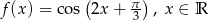 .
.
- Narysuj wykres funkcji
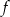 dla
dla 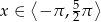 .
. - Rozwiąż równanie:
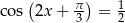 , dla
, dla 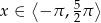 .
.
Pierwszy wyraz nieskończonego ciągu geometrycznego 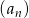 jest równy
jest równy 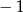 . Wyraz drugi, trzeci i czwarty spełniają warunek
. Wyraz drugi, trzeci i czwarty spełniają warunek 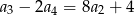 .
.
- Oblicz iloraz ciągu
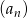 .
. - Określ, czy ciąg
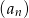 jest rosnący, czy malejący.
jest rosnący, czy malejący.
W ciągu arytmetycznym 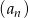 , określonym dla
, określonym dla 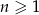 , dane są: wyraz
, dane są: wyraz 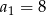 i suma trzech początkowych wyrazów tego ciągu
i suma trzech początkowych wyrazów tego ciągu 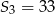 . Oblicz różnicę
. Oblicz różnicę 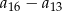 .
.
W ciągu arytmetycznym 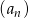 , określonym dla
, określonym dla 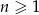 , dane są: wyraz
, dane są: wyraz 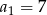 i suma czterech początkowych wyrazów tego ciągu
i suma czterech początkowych wyrazów tego ciągu 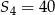 . Oblicz różnicę
. Oblicz różnicę 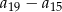 .
.
Wykaż, że jeżeli wielomian 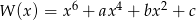 jest podzielny przez trójmian
jest podzielny przez trójmian 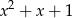 , to jest również podzielny przez trójmian
, to jest również podzielny przez trójmian 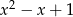 .
.
Wielomian 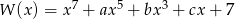 jest podzielny przez wielomian
jest podzielny przez wielomian 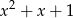 . Wyznacz resztę z dzielenia wielomianu
. Wyznacz resztę z dzielenia wielomianu 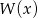 przez wielomian
przez wielomian 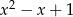 .
.
Tworząca stożka jest nachylona do podstawy pod kątem  . Kula opisana na tym stożku ma promień
. Kula opisana na tym stożku ma promień 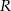 . Oblicz pole powierzchni całkowitej tego stożka.
. Oblicz pole powierzchni całkowitej tego stożka.
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 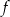 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 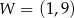 . Liczby
. Liczby 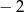 i 4 to miejsca zerowe funkcji
i 4 to miejsca zerowe funkcji 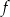 .
.
Zbiorem wartości funkcji 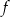 jest przedział
jest przedział
A) 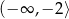 B)
B) 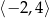 C)
C) 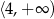 D)
D) 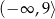
Na rysunku przedstawiono fragment paraboli będącej wykresem funkcji kwadratowej 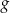 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 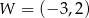 .
.
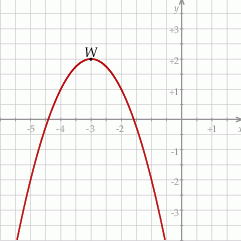
Zbiorem wartości funkcji 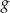 jest przedział
jest przedział
A) 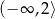 B)
B) 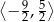 C)
C) 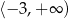 D)
D) 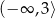
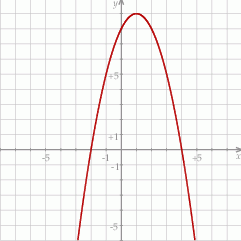
W kartezjańskim układzie współrzędnych 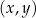 przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej
przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej 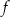 (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osią
(zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osią 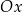 układu współrzędnych mają obie współrzędne całkowite.
układu współrzędnych mają obie współrzędne całkowite.
Zbiorem wartości funkcji 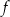 jest przedział
jest przedział
A) ![(− ∞ ,− 2]](https://img.zadania.info/zad/8329959/HzadT5x.png) B)
B) 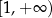 C)
C) ![[− 1,3]](https://img.zadania.info/zad/8329959/HzadT7x.png) D)
D) 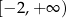
W kartezjańskim układzie współrzędnych 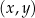 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 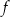 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 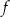 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
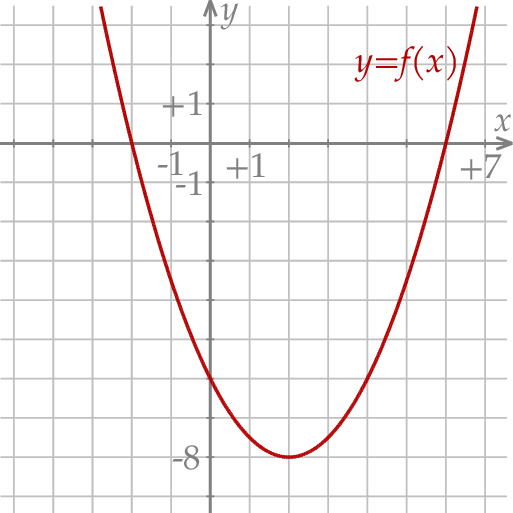
Zbiorem wartości funkcji 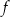 jest przedział
jest przedział
A) ![(− ∞ ,2]](https://img.zadania.info/zad/5942619/HzadT5x.png) B)
B) ![(− ∞ ,− 8]](https://img.zadania.info/zad/5942619/HzadT6x.png) C)
C) 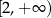 D)
D) 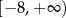
W kartezjańskim układzie współrzędnych 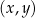 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 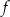 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 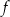 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
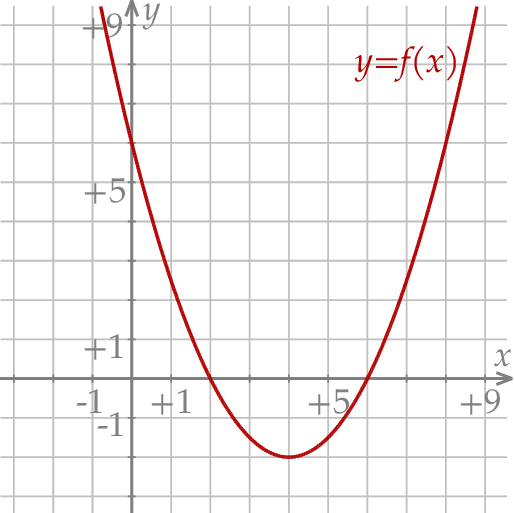
Zbiorem wartości funkcji 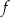 jest przedział
jest przedział
A) ![(− ∞ ,− 2]](https://img.zadania.info/zad/7004661/HzadT5x.png) B)
B) ![(− ∞ ,4]](https://img.zadania.info/zad/7004661/HzadT6x.png) C)
C) 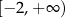 D)
D) 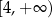
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 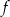 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 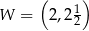 . Liczby
. Liczby 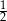 i
i 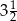 to miejsca zerowe funkcji
to miejsca zerowe funkcji 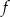 .
.
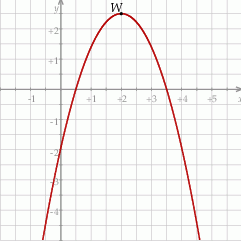
Zbiorem wartości funkcji 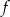 jest przedział
jest przedział
A) 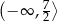 B)
B) 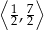 C)
C) 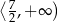 D)
D) 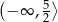
Na rysunku przedstawiono fragment paraboli będącej wykresem funkcji kwadratowej 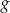 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 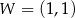 .
.
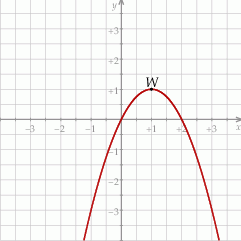
Zbiorem wartości funkcji 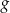 jest przedział
jest przedział
A) 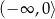 B)
B) 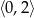 C)
C) 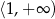 D)
D) 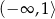
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 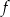 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 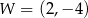 . Liczby 0 i 4 to miejsca zerowe funkcji
. Liczby 0 i 4 to miejsca zerowe funkcji 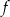 .
.
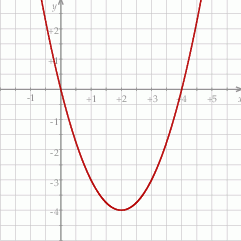
Zbiorem wartości funkcji 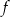 jest przedział
jest przedział
A) 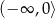 B)
B) 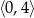 C)
C) 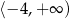 D)
D) 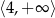
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 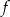 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 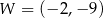 . Liczby
. Liczby 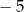 i 1 to miejsca zerowe funkcji
i 1 to miejsca zerowe funkcji 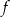 .
.
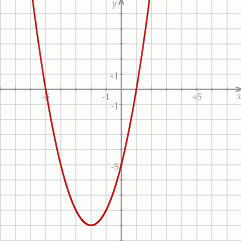
Zbiorem wartości funkcji 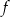 jest przedział
jest przedział
A) 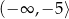 B)
B) 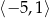 C)
C) 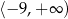 D)
D) 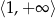
Oblicz długości boków trójkąta prostokątnego wiedząc, że długości przyprostokątnych różnią się o 9 cm, a jego pole jest równe 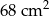 .
.
Oblicz obwód trójkąta prostokątnego o polu powierzchni równym 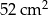 , wiedząc, że długości jego przyprostokątnych różnią się o 5 cm.
, wiedząc, że długości jego przyprostokątnych różnią się o 5 cm.
Pole trójkąta prostokątnego jest równe 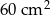 . Jedna przyprostokątna jest o 7 cm dłuższa od drugiej. Oblicz długość przeciwprostokątnej tego trójkąta.
. Jedna przyprostokątna jest o 7 cm dłuższa od drugiej. Oblicz długość przeciwprostokątnej tego trójkąta.
Oblicz obwód trójkąta prostokątnego o polu powierzchni równym 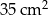 , wiedząc, że długości jego przyprostokątnych różnią się o 3 cm.
, wiedząc, że długości jego przyprostokątnych różnią się o 3 cm.
Oblicz długości boków trójkąta prostokątnego o polu powierzchni równym 20, wiedząc, że długości jego przyprostokątnych różnią się o 6.
Pole trójkąta prostokątnego jest równe 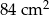 . Jedna przyprostokątna jest o 17 cm dłuższa od drugiej. Oblicz długość przeciwprostokątnej tego trójkąta.
. Jedna przyprostokątna jest o 17 cm dłuższa od drugiej. Oblicz długość przeciwprostokątnej tego trójkąta.
Oblicz długości boków trójkąta prostokątnego o polu powierzchni równym 5, wiedząc, że długości jego przyprostokątnych różnią się o 3.
Danych jest osiem kul z numerami od 1 do 8, oraz dziesięć szuflad z numerami od 1 do 10. Rozmieszczamy w dowolny sposób kule w szufladach. Oblicz prawdopodobieństwa następujących zdarzeń:
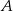 – wszystkie kule znajdą się w szufladach z numerami parzystymi.
– wszystkie kule znajdą się w szufladach z numerami parzystymi. 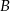 – dokładnie dwie szuflady pozostaną puste.
– dokładnie dwie szuflady pozostaną puste.
Gracz rzuca dwa razy symetryczną sześcienną kostką do gry i oblicza iloczyn wyrzucanych oczek. Jeśli iloczyn ten jest liczbą podzielną przez 2 lub przez 3 to przegrywa. W pozostałych przypadkach wygrywa.
- Uzupełnij tabelkę tak, aby przedstawiała wszystkie wyniki tego doświadczenia.
- Podaj liczbę wynikow sprzyjających wygranej gracza i oblicz prawdopodobieństwo wygranej.
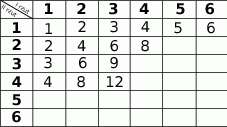
Spawacz ma wykonać z blachy konstrukcję, która powstaje przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego trójkątnego. Wymiary elementów są podane na rysunku.
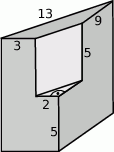
- Oblicz objętość tej konstrukcji.
- Oblicz łączne pole powierzchni wszystkich 7 ścian otrzymanej bryły. Wynik podaj z zaokrągleniem do
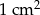 .
.
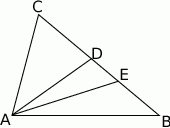
Na boku 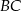 trójkąta
trójkąta 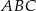 wybrano punkt
wybrano punkt  tak, by
tak, by 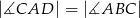 . Odcinek
. Odcinek 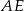 jest dwusieczną kąta
jest dwusieczną kąta 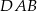 . Udowodnij, że
. Udowodnij, że 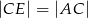 .
.
Po torze wodnym o długości 10 km pływają w kółko dwie łodzie motorowe, przy czym druga z nich płynie z prędkością o 5 km/h większą od prędkości pierwszej łodzi. Łodzie te wystartowały z tego samego punktu i ponownie spotkały się, gdy pierwsza z łodzi wykonała pełne 3 okrążenia toru. Oblicz średnie prędkości obu łodzi.
Trasa rowerowa wokół jeziora ma długość 12 kilometrów. Dwóch rowerzystów wyrusza z tego samego miejsca i okrąża jezioro w tym samym kierunku. Średnia prędkość jednego z nich jest o 4 km/h mniejsza niż prędkość drugiego rowerzysty. Do ponownego spotkania rowerzystów doszło, gdy szybszy z nich wykonał 4 okrążenia jeziora. Jakie były średnie prędkości rowerzystów?
Liczba wszystkich krawędzi graniastosłupa jest równa 24. Wówczas podstawą tego graniastosłupa jest:
A) sześciokąt B) ośmiokąt C) dziesięciokąt D) dwunastokąt
Liczba wszystkich krawędzi graniastosłupa jest równa 21. Wówczas podstawą tego graniastosłupa jest:
A) sześciokąt B) ośmiokąt C) siedmiokąt D) dwunastokąt
Liczby 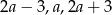 , w podanej kolejności, tworzą ciąg geometryczny. Wyznacz
, w podanej kolejności, tworzą ciąg geometryczny. Wyznacz  .
.
Trójwyrazowy ciąg 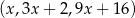 jest geometryczny. Oblicz
jest geometryczny. Oblicz  .
.
Dany jest trzywyrazowy ciąg 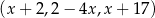 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Dany jest trzywyrazowy ciąg 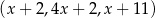 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Spośród wyrazów skończonego ciągu arytmetycznego 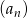 danego wzorem
danego wzorem 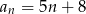 , gdzie
, gdzie 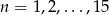 wybieramy losowo 3. Oblicz prawdopodobieństwo, że iloczyn wybranych liczb jest podzielny przez 3.
wybieramy losowo 3. Oblicz prawdopodobieństwo, że iloczyn wybranych liczb jest podzielny przez 3.

