Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej  . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt  . Liczby
. Liczby  i 4 to miejsca zerowe funkcji
i 4 to miejsca zerowe funkcji  .
.
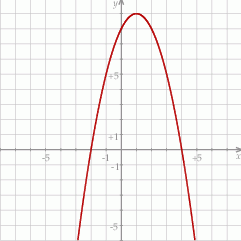
Zbiorem wartości funkcji 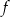 jest przedział
jest przedział
A) 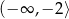 B)
B) 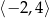 C)
C) 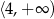 D)
D) 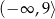
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 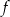 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 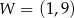 . Liczby
. Liczby 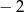 i 4 to miejsca zerowe funkcji
i 4 to miejsca zerowe funkcji 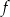 .
.

Zbiorem wartości funkcji 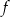 jest przedział
jest przedział
A) 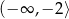 B)
B) 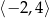 C)
C) 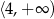 D)
D) 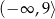
Na rysunku przedstawiono fragment paraboli będącej wykresem funkcji kwadratowej 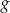 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 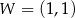 .
.
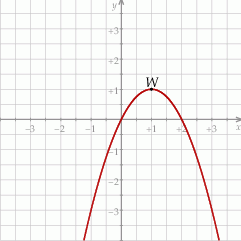
Zbiorem wartości funkcji 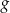 jest przedział
jest przedział
A) 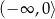 B)
B) 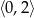 C)
C) 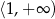 D)
D) 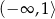
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 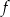 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 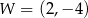 . Liczby 0 i 4 to miejsca zerowe funkcji
. Liczby 0 i 4 to miejsca zerowe funkcji 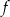 .
.
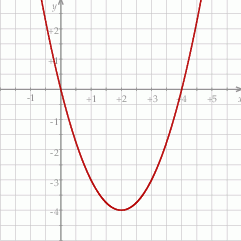
Zbiorem wartości funkcji 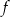 jest przedział
jest przedział
A) 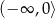 B)
B) 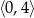 C)
C) 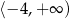 D)
D) 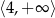
Na rysunku przedstawiono fragment paraboli będącej wykresem funkcji kwadratowej 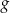 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 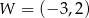 .
.
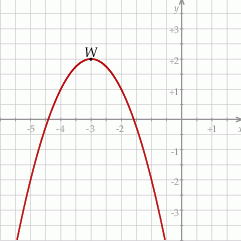
Zbiorem wartości funkcji 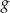 jest przedział
jest przedział
A) 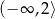 B)
B) 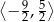 C)
C) 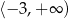 D)
D) 
W kartezjańskim układzie współrzędnych 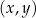 przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej
przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej 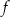 (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osią
(zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osią 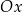 układu współrzędnych mają obie współrzędne całkowite.
układu współrzędnych mają obie współrzędne całkowite.
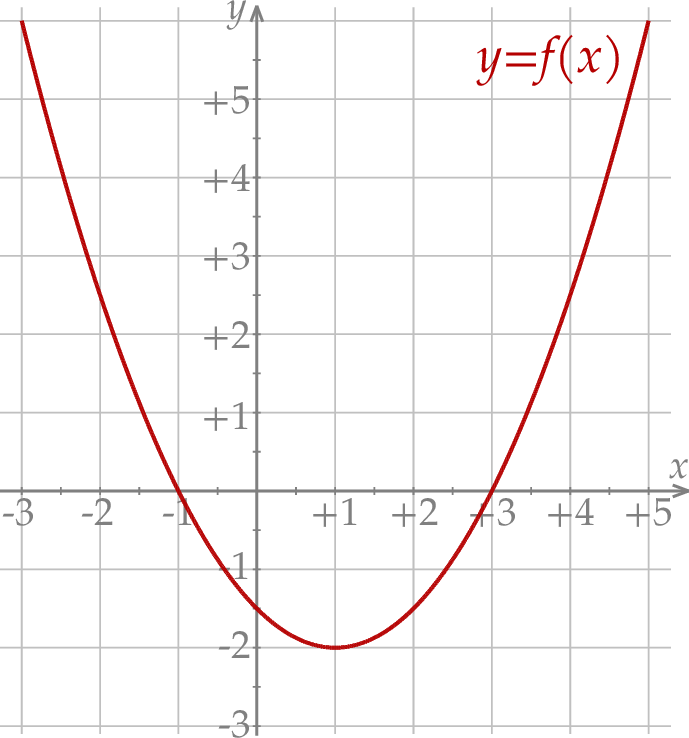
Zbiorem wartości funkcji 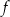 jest przedział
jest przedział
A) ![(− ∞ ,− 2]](https://img.zadania.info/zad/8329959/HzadT5x.png) B)
B) 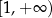 C)
C) ![[− 1,3]](https://img.zadania.info/zad/8329959/HzadT7x.png) D)
D) 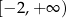
W kartezjańskim układzie współrzędnych 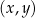 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 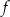 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 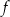 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
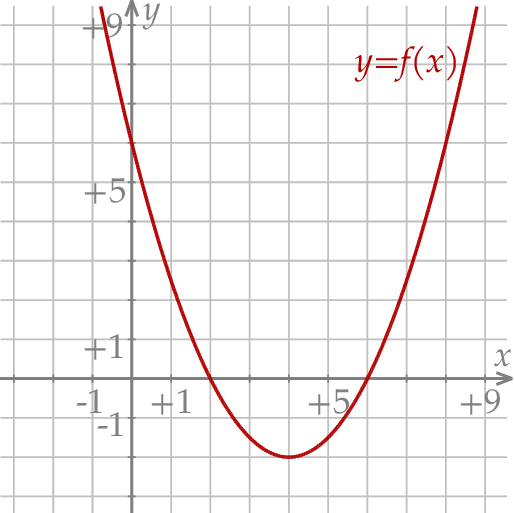
Zbiorem wartości funkcji 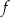 jest przedział
jest przedział
A) ![(− ∞ ,− 2]](https://img.zadania.info/zad/7004661/HzadT5x.png) B)
B) ![(− ∞ ,4]](https://img.zadania.info/zad/7004661/HzadT6x.png) C)
C) 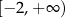 D)
D) 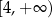
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 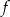 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 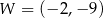 . Liczby
. Liczby 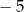 i 1 to miejsca zerowe funkcji
i 1 to miejsca zerowe funkcji 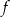 .
.
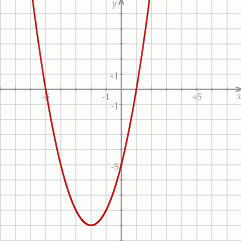
Zbiorem wartości funkcji 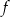 jest przedział
jest przedział
A) 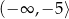 B)
B) 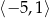 C)
C) 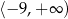 D)
D) 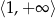
W kartezjańskim układzie współrzędnych 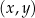 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 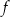 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 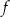 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
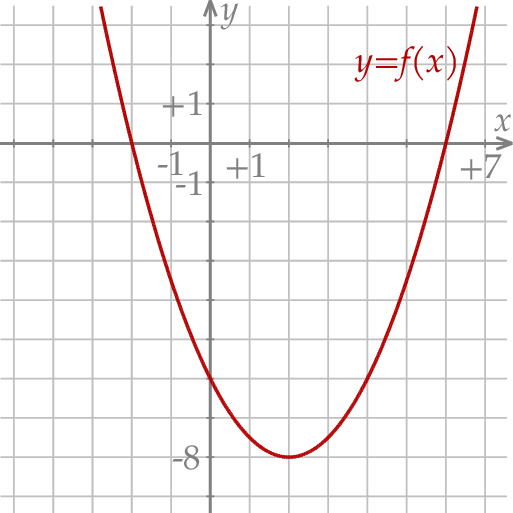
Zbiorem wartości funkcji 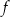 jest przedział
jest przedział
A) ![(− ∞ ,2]](https://img.zadania.info/zad/5942619/HzadT5x.png) B)
B) ![(− ∞ ,− 8]](https://img.zadania.info/zad/5942619/HzadT6x.png) C)
C) 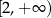 D)
D) 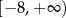
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 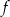 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 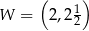 . Liczby
. Liczby 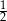 i
i 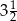 to miejsca zerowe funkcji
to miejsca zerowe funkcji 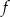 .
.
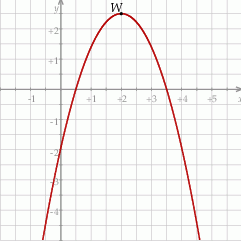
Zbiorem wartości funkcji 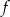 jest przedział
jest przedział
A) 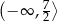 B)
B) 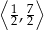 C)
C) 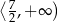 D)
D) 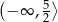
Oblicz długości boków trójkąta prostokątnego wiedząc, że długości przyprostokątnych różnią się o 9 cm, a jego pole jest równe 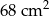 .
.
Oblicz obwód trójkąta prostokątnego o polu powierzchni równym 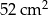 , wiedząc, że długości jego przyprostokątnych różnią się o 5 cm.
, wiedząc, że długości jego przyprostokątnych różnią się o 5 cm.
Pole trójkąta prostokątnego jest równe 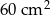 . Jedna przyprostokątna jest o 7 cm dłuższa od drugiej. Oblicz długość przeciwprostokątnej tego trójkąta.
. Jedna przyprostokątna jest o 7 cm dłuższa od drugiej. Oblicz długość przeciwprostokątnej tego trójkąta.
Oblicz obwód trójkąta prostokątnego o polu powierzchni równym 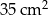 , wiedząc, że długości jego przyprostokątnych różnią się o 3 cm.
, wiedząc, że długości jego przyprostokątnych różnią się o 3 cm.
Oblicz długości boków trójkąta prostokątnego o polu powierzchni równym 20, wiedząc, że długości jego przyprostokątnych różnią się o 6.
Pole trójkąta prostokątnego jest równe 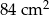 . Jedna przyprostokątna jest o 17 cm dłuższa od drugiej. Oblicz długość przeciwprostokątnej tego trójkąta.
. Jedna przyprostokątna jest o 17 cm dłuższa od drugiej. Oblicz długość przeciwprostokątnej tego trójkąta.
Oblicz długości boków trójkąta prostokątnego o polu powierzchni równym 5, wiedząc, że długości jego przyprostokątnych różnią się o 3.
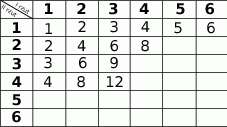
Danych jest osiem kul z numerami od 1 do 8, oraz dziesięć szuflad z numerami od 1 do 10. Rozmieszczamy w dowolny sposób kule w szufladach. Oblicz prawdopodobieństwa następujących zdarzeń:
 – wszystkie kule znajdą się w szufladach z numerami parzystymi.
– wszystkie kule znajdą się w szufladach z numerami parzystymi.  – dokładnie dwie szuflady pozostaną puste.
– dokładnie dwie szuflady pozostaną puste.Gracz rzuca dwa razy symetryczną sześcienną kostką do gry i oblicza iloczyn wyrzucanych oczek. Jeśli iloczyn ten jest liczbą podzielną przez 2 lub przez 3 to przegrywa. W pozostałych przypadkach wygrywa.
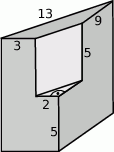
Spawacz ma wykonać z blachy konstrukcję, która powstaje przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego trójkątnego. Wymiary elementów są podane na rysunku.
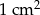 .
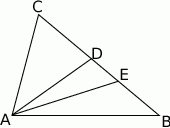
.Na boku 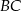 trójkąta
trójkąta 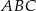 wybrano punkt
wybrano punkt 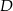 tak, by
tak, by 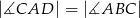 . Odcinek
. Odcinek 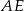 jest dwusieczną kąta
jest dwusieczną kąta 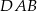 . Udowodnij, że
. Udowodnij, że 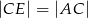 .
.
Po torze wodnym o długości 10 km pływają w kółko dwie łodzie motorowe, przy czym druga z nich płynie z prędkością o 5 km/h większą od prędkości pierwszej łodzi. Łodzie te wystartowały z tego samego punktu i ponownie spotkały się, gdy pierwsza z łodzi wykonała pełne 3 okrążenia toru. Oblicz średnie prędkości obu łodzi.
Trasa rowerowa wokół jeziora ma długość 12 kilometrów. Dwóch rowerzystów wyrusza z tego samego miejsca i okrąża jezioro w tym samym kierunku. Średnia prędkość jednego z nich jest o 4 km/h mniejsza niż prędkość drugiego rowerzysty. Do ponownego spotkania rowerzystów doszło, gdy szybszy z nich wykonał 4 okrążenia jeziora. Jakie były średnie prędkości rowerzystów?
Liczba wszystkich krawędzi graniastosłupa jest równa 24. Wówczas podstawą tego graniastosłupa jest:
A) sześciokąt B) ośmiokąt C) dziesięciokąt D) dwunastokąt
Liczba wszystkich krawędzi graniastosłupa jest równa 21. Wówczas podstawą tego graniastosłupa jest:
A) sześciokąt B) ośmiokąt C) siedmiokąt D) dwunastokąt
Liczby 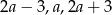 , w podanej kolejności, tworzą ciąg geometryczny. Wyznacz
, w podanej kolejności, tworzą ciąg geometryczny. Wyznacz  .
.
Trójwyrazowy ciąg 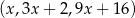 jest geometryczny. Oblicz
jest geometryczny. Oblicz  .
.
Dany jest trzywyrazowy ciąg 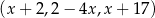 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Dany jest trzywyrazowy ciąg 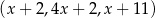 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Spośród wyrazów skończonego ciągu arytmetycznego 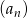 danego wzorem
danego wzorem 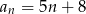 , gdzie
, gdzie 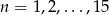 wybieramy losowo 3. Oblicz prawdopodobieństwo, że iloczyn wybranych liczb jest podzielny przez 3.
wybieramy losowo 3. Oblicz prawdopodobieństwo, że iloczyn wybranych liczb jest podzielny przez 3.
Firma obuwnicza otrzymała zamówienie na wykonanie 720 par butów. Aby zrealizować zamówienie na czas, postanowiono wykonywać dziennie jednakową liczbę par butów. Po wykonaniu 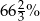 zamówienia usprawniono produkcję tak, że dzienna produkcja wzrosła o 4 pary, zaś zamówienie zrealizowano o 5 dni wcześniej. W ciągu ilu dni planowano wykonać zamówienie?
zamówienia usprawniono produkcję tak, że dzienna produkcja wzrosła o 4 pary, zaś zamówienie zrealizowano o 5 dni wcześniej. W ciągu ilu dni planowano wykonać zamówienie?
Firma odzieżowa otrzymała zamówienie na wykonanie 600 kurtek. Aby zrealizować zamówienie firma postanowiła wykonywać dziennie tę samą liczbę kurtek. Po wykonaniu 60% zamówienia usprawniono produkcję tak, że dzienna produkcja wzrosła o 6 kurtek, zaś zamówienie zrealizowano o 2 dni wcześniej w stosunku do pierwotnego planu. W ciągu ilu dni zrealizowano zamówienie?
Wielomian 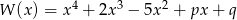 jest podzielny przez dwumian
jest podzielny przez dwumian 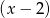 , a przy dzieleniu przez
, a przy dzieleniu przez 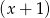 daje resztę
daje resztę 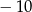 . Wyznacz
. Wyznacz 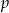 i
i 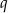 .
.
Wielomian 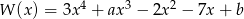 jest podzielny przez dwumian
jest podzielny przez dwumian 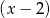 , a przy dzieleniu przez
, a przy dzieleniu przez 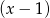 daje resztę 3. Wyznacz
daje resztę 3. Wyznacz  i
i 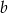 .
.
Rozwiąż układ równań:
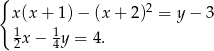
Rozwiąż układ równań 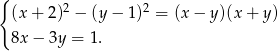
Rozwiąż układ równań 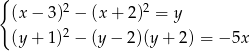
Dany jest punkt 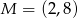 . Wyznacz równanie takiej prostej
. Wyznacz równanie takiej prostej 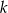 , do której należy punkt
, do której należy punkt 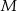 , że na ujemnej półosi
, że na ujemnej półosi 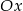 i dodatniej półosi
i dodatniej półosi 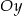 układu
układu 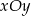 prosta ta wyznacza odcinki
prosta ta wyznacza odcinki 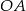 i
i 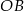 , których suma długości jest równa 6. Oblicz obwód trójkąta
, których suma długości jest równa 6. Oblicz obwód trójkąta 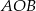 .
.
Oblicz sumę szeregu
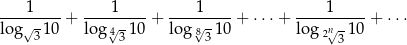
Rozwiąż równanie 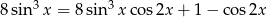 w przedziale
w przedziale 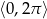 .
.
Miary kątów trójkąta są w stosunku 1:2:3. Obwód koła opisanego na tym trójkącie jest równy 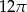 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
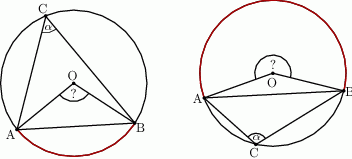
Oblicz miary kątów środkowych 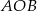 zaznaczonych na rysunkach, jeśli dana jest miara kąta wpisanego
zaznaczonych na rysunkach, jeśli dana jest miara kąta wpisanego 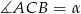 .
.
Kąt środkowy oparty na łuku, którego długość jest równa 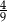 długości okręgu, ma miarę
długości okręgu, ma miarę
A) 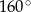 B)
B) 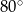 C)
C) 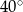 D)
D) 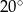
Kąt środkowy oparty na łuku, którego długość jest równa  długości okręgu, ma miarę
długości okręgu, ma miarę
A) 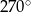 B)
B) 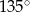 C)
C) 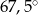 D)
D) 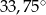
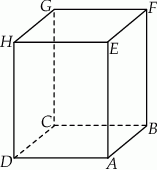
W graniastosłupie prawidłowym czworokątnym 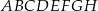 połączono punkty będące środkami krawędzi
połączono punkty będące środkami krawędzi 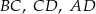 i
i 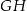 . Wyznacz objętość powstałej bryły wiedząc, że
. Wyznacz objętość powstałej bryły wiedząc, że 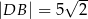 i kąt
i kąt 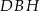 ma miarę
ma miarę 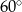 .
.