Liczby rzeczywiste  i
i 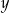 są dodatnie oraz
są dodatnie oraz 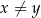 . Wyrażenie
. Wyrażenie 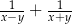 można przekształcić do postaci
można przekształcić do postaci
A) 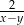 B)
B) 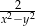 C)
C) 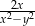 D)
D) 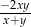
/Szkoła średnia
Liczby rzeczywiste  i
i 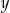 są dodatnie oraz
są dodatnie oraz 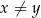 . Wyrażenie
. Wyrażenie 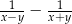 można przekształcić do postaci
można przekształcić do postaci
A) 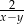 B)
B) 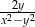 C)
C) 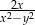 D)
D) 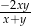
Suma dwóch liczb równa jest 6. Znajdź te liczby, jeśli wiadomo, że suma podwojonego kwadratu jednej z nich i kwadratu drugiej jest najmniejsza z możliwych.
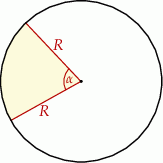
Z papierowego koła o promieniu 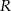 wycięto wycinek kołowy, który jest powierzchnią boczną stożka o maksymalnej objętości. Jaka była miara kąta środkowego
wycięto wycinek kołowy, który jest powierzchnią boczną stożka o maksymalnej objętości. Jaka była miara kąta środkowego  wyciętego wycinka? Wynik podaj w radianach.
wyciętego wycinka? Wynik podaj w radianach.
Ze zbioru liczb 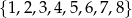 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 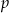 jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
A) 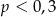 B)
B) 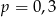 C)
C) 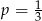 D)
D) 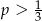
Ze zbioru 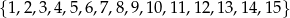 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 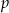 oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 4. Wówczas
oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 4. Wówczas
A) 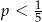 B)
B) 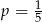 C)
C) 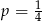 D)
D) 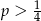
Ze zbioru liczb 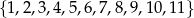 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 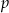 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A) 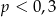 B)
B) 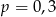 C)
C) 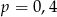 D)
D) 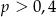
Ze zbioru liczb 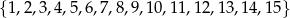 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 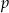 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A) 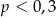 B)
B) 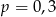 C)
C) 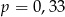 D)
D) 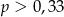
Ze zbioru liczb 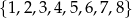 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 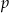 oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
A) 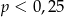 B)
B) 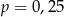 C)
C) 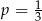 D)
D) 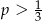
W romb o boku  wpisano dwa okręgi w ten sposób, że okręgi te są styczne zewnętrznie i każdy z nich jest styczny do dwóch sąsiednich boków rombu przecinających się pod kątem ostrym
wpisano dwa okręgi w ten sposób, że okręgi te są styczne zewnętrznie i każdy z nich jest styczny do dwóch sąsiednich boków rombu przecinających się pod kątem ostrym  (zobacz rysunek).
(zobacz rysunek).
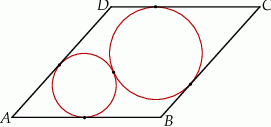
Udowodnij, że suma promieni tych okręgów jest równa 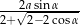 .
.
Podstawą ostrosłupa 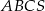 jest trójkąt
jest trójkąt 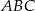 o bokach długości 18 cm i 12 cm, którego kąt między tymi bokami ma miarę równą
o bokach długości 18 cm i 12 cm, którego kąt między tymi bokami ma miarę równą 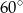 . Wszystkie krawędzie boczne ostrosłupa
. Wszystkie krawędzie boczne ostrosłupa 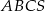 mają długości równe 12 cm. Ostrosłup ten przecięto płaszczyzną równoległą do podstawy i dzielącą jego wysokość w stosunku 1:2, licząc od wierzchołka tego ostrosłupa. Wykonaj rysunek ostrosłupa
mają długości równe 12 cm. Ostrosłup ten przecięto płaszczyzną równoległą do podstawy i dzielącą jego wysokość w stosunku 1:2, licząc od wierzchołka tego ostrosłupa. Wykonaj rysunek ostrosłupa 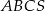 z zaznaczonym przekrojem i oblicz:
z zaznaczonym przekrojem i oblicz:
- obwód otrzymanego przekroju,
- objętość tej z brył wyznaczonych przez przekrój, która nie jest podobna do ostrosłupa
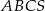 .
.
Ciągiem geometrycznym o ilorazie 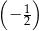 jest ciąg określony wzorem
jest ciąg określony wzorem
A) 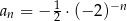 B)
B) 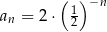 C)
C) 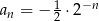 D)
D) 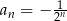
W pudełku znajduje się 8 piłeczek oznaczonych kolejnymi liczbami naturalnymi od 1 do 8. Losujemy jedną piłeczkę, zapisujemy liczbę na niej występującą, a następnie zwracamy piłeczkę do urny. Tę procedurę wykonujemy jeszcze dwa razy i tym samym otrzymujemy zapisane trzy liczby. Oblicz prawdopodobieństwo wylosowania takich piłeczek, że iloczyn trzech zapisanych liczb jest podzielny przez 4. Wynik podaj w postaci ułamka zwykłego.
Oblicz granicę 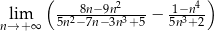 .
.
Wyrażenie 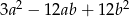 może być przekształcone do postaci
może być przekształcone do postaci
A) 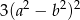 B)
B) 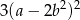 C)
C) 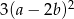 D)
D) 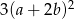
Wyrażenie 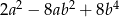 może być przekształcone do postaci
może być przekształcone do postaci
A) 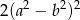 B)
B) 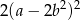 C)
C) 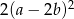 D)
D) 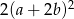
Udowodnij, że w trójkącie prostokątnym dwusieczna kąta prostego dzieli na połowy kąt zawarty między środkową, a wysokością opuszczoną z wierzchołka kąta prostego.
Liczba 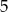 nie należy do dziedziny wyrażenia
nie należy do dziedziny wyrażenia
A) 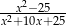 B)
B) 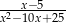 C)
C) 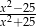 D)
D) 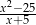
Liczba -5 nie należy do dziedziny wyrażenia
A) 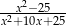 B)
B) 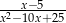 C)
C) 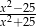 D)
D) 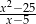
Liczba 3 nie należy do dziedziny wyrażenia
A) 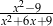 B)
B) 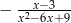 C)
C) 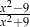 D)
D) 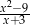
Liczba 4 nie należy do dziedziny wyrażenia
A) 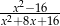 B)
B) 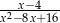 C)
C) 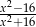 D)
D) 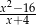
Dla 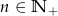 zawsze nieparzysta jest liczba
zawsze nieparzysta jest liczba
A)  B)
B) 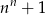 C)
C) 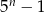 D)
D) 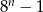
Dla 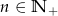 zawsze nieparzysta jest liczba
zawsze nieparzysta jest liczba
A) 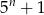 B)
B) 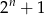 C)
C) 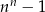 D)
D) 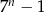
Dla 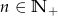 zawsze parzysta jest liczba
zawsze parzysta jest liczba
A) 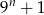 B)
B) 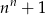 C)
C) 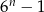 D)
D) 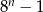
Funkcja 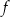 jest określona wzorem
jest określona wzorem 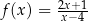 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 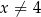 . W kartezjańskim układzie współrzędnych
. W kartezjańskim układzie współrzędnych 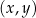 punkt
punkt 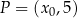 należy do wykresu funkcji
należy do wykresu funkcji 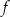 . Oblicz
. Oblicz 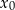 oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji 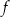 w punkcie
w punkcie 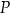 .
.
Średnia arytmetyczna pięciu liczb: 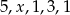 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 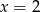 B)
B) 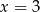 C)
C) 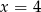 D)
D) 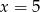
Średnia arytmetyczna dziesięciu liczb 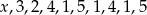 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 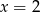 B)
B) 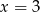 C)
C) 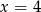 D)
D) 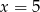
Średnia arytmetyczna zestawu sześciu liczb: 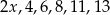 , jest równa 5. Wynika stąd, że
, jest równa 5. Wynika stąd, że
A) 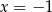 B)
B) 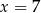 C)
C) 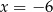 D)
D) 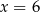
Średnia arytmetyczna siedmiu liczb: 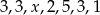 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 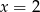 B)
B) 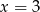 C)
C) 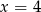 D)
D) 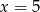
Średnia arytmetyczna pięciu liczb: 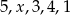 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 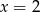 B)
B) 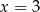 C)
C) 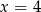 D)
D) 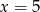
Średnia arytmetyczna zestawu danych: 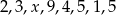 wynosi 4,5. Wynika z tego, że:
wynosi 4,5. Wynika z tego, że:
A) 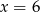 B)
B) 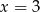 C)
C) 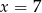 D)
D) 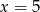
Średnia arytmetyczna ośmiu liczb: 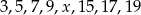 jest równa 11. Wtedy
jest równa 11. Wtedy
A) 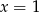 B)
B) 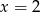 C)
C) 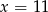 D)
D) 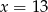
Średnia arytmetyczna pięciu liczb: 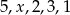 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 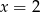 B)
B) 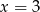 C)
C) 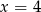 D)
D) 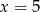
Średnia arytmetyczna sześciu liczb: 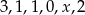 jest równa 2. Wtedy liczba
jest równa 2. Wtedy liczba  jest równa
jest równa
A) 3 B) 4 C) 5 D) 6
Średnia arytmetyczna pięciu liczb: 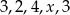 jest równa 3,2. Wtedy
jest równa 3,2. Wtedy
A) 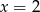 B)
B) 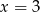 C)
C) 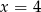 D)
D) 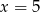
Dla jakiej wartości liczbowej  średnia arytmetyczna liczb:
średnia arytmetyczna liczb: 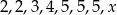 jest równa 4?
jest równa 4?
A) 6 B) 5 C) 4 D) 3
Średnia arytmetyczna zestawu danych: 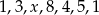 wynosi 4. Wynika z tego, że:
wynosi 4. Wynika z tego, że:
A) 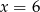 B)
B) 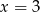 C)
C) 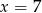 D)
D) 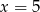
Średnia arytmetyczna liczb 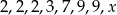 jest równa 4,5. Liczba
jest równa 4,5. Liczba  jest równa
jest równa
A) 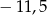 B) 1 C) 1,5 D) 2
B) 1 C) 1,5 D) 2
Średnia arytmetyczna dziesięciu liczb 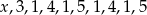 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 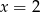 B)
B) 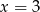 C)
C) 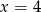 D)
D) 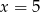
Średnia arytmetyczna liczb: 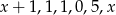 jest równa
jest równa  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A)  B) 2 C)
B) 2 C)  D)
D) 
Średnia arytmetyczna zestawu danych: 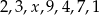 wynosi
wynosi 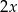 . Wynika z tego, że:
. Wynika z tego, że:
A) 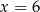 B)
B) 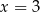 C)
C) 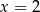 D)
D) 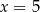
W trójkącie prostokątnym dany jest kąt ostry o mierze  i pole
i pole 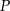 tego trójkąta. Obliczyć długość środkowej poprowadzonej z wierzchołka kąta prostego.
tego trójkąta. Obliczyć długość środkowej poprowadzonej z wierzchołka kąta prostego.
Rowerzysta jedzie ze stałą prędkością 20km/h.
- Napisz wzór wyrażający drogę
 rowerzysty w ciągu
rowerzysty w ciągu 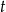 godzin.
godzin. - Sporządź tabelkę wartości
 dla
dla 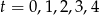 .
. - Naszkicuj wykres zależności
 od
od 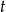 .
.
Wyznacz te wartości parametru 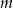 , dla których równanie
, dla których równanie
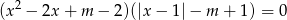
ma dokładnie trzy pierwiastki rzeczywiste? Oblicz te pierwiastki.
Objętość ostrosłupa prawidłowego trójkątnego 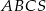 jest równa
jest równa 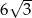 , a krawędź boczna tworzy z płaszczyzną podstawy kąt
, a krawędź boczna tworzy z płaszczyzną podstawy kąt 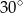 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
Dany jest nieskończony ciąg geometryczny 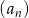 , który zawiera zarówno wyrazy dodatnie, jak i ujemne, w którym
, który zawiera zarówno wyrazy dodatnie, jak i ujemne, w którym 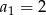 , oraz drugi, czwarty i piąty wyraz są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że suma sześcianów wszystkich wyrazów ciągu
, oraz drugi, czwarty i piąty wyraz są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że suma sześcianów wszystkich wyrazów ciągu 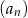 jest równa sumie kwadratów wszystkich wyrazów tego ciągu.
jest równa sumie kwadratów wszystkich wyrazów tego ciągu.

