Liczba miejsc zerowych funkcji 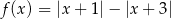 , gdzie
, gdzie 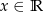 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
/Szkoła średnia
Funkcja 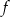 przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb:
przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb: 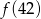 ,
, 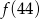 ,
, 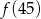 ,
, 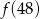 największa to
największa to
A) 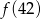 B)
B) 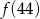 C)
C) 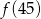 D)
D) 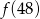
Funkcja 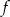 przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb:
przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb: 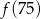 ,
, 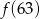 ,
, 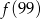 ,
, 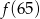 największa to
największa to
A) 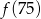 B)
B) 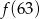 C)
C) 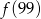 D)
D) 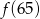
W ciągu arytmetycznym 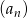 wyraz
wyraz 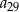 jest dwa razy większy od wyrazu
jest dwa razy większy od wyrazu 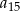 oraz
oraz 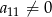 . Wtedy iloraz
. Wtedy iloraz 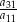 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
W ciągu arytmetycznym 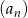 wyraz
wyraz 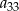 jest dwa razy większy od wyrazu
jest dwa razy większy od wyrazu 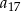 oraz
oraz 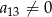 . Wtedy iloraz
. Wtedy iloraz 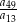 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
Jeżeli 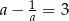 to liczba
to liczba 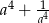 jest równa
jest równa
A) 121 B) 119 C) 123 D) 81
Jeżeli 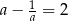 , to liczba
, to liczba 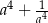 jest równa
jest równa
A) 36 B) 34 C) 6 D) 16
Jeżeli 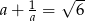 to liczba
to liczba 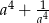 jest równa
jest równa
A) 16 B) 6 C) 14 D) 36
Ze zbioru 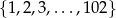 losujemy 2 różne liczby. Jakie jest prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3?
losujemy 2 różne liczby. Jakie jest prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3?
Rozwiąż nierówność 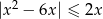 .
.
Pole powierzchni bocznej ostrosłupa prawidłowego trójkątnego równa się 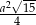 , gdzie
, gdzie  oznacza długość krawędzi podstawy tego ostrosłupa. Zaznacz na poniższym rysunku kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy. Miarę tego kąta oznacz symbolem
oznacza długość krawędzi podstawy tego ostrosłupa. Zaznacz na poniższym rysunku kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy. Miarę tego kąta oznacz symbolem 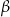 . Oblicz
. Oblicz 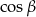 i korzystając z tablic funkcji trygonometrycznych i odczytaj przybliżoną wartość
i korzystając z tablic funkcji trygonometrycznych i odczytaj przybliżoną wartość 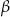 z dokładnością do
z dokładnością do 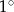 .
.
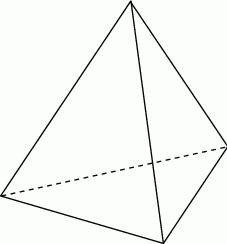
Dany jest ostrosłup prawidłowy czworokątny 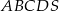 o podstawie
o podstawie 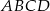 . Pole trójkąta
. Pole trójkąta 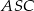 jest równe 120, a cosinus kąta
jest równe 120, a cosinus kąta 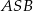 jest równy
jest równy 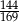 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
W pewnym zakładzie pracy w wyniku dwóch podwyżek zwiększono pensje pracowników o 26%. W ramach pierwszej z tych podwyżek płace zwiększono o 20%. O ile procent zwiększono płace w ramach drugiej podwyżki?
A) o 12% B) o 6% C) o 5% D) o 10%
W wyniku dwóch obniżek cenę spodni obniżono o 52%. W ramach pierwszej z tych obniżek cenę zmniejszono o 20%. O ile procent zmniejszono cenę w ramach drugiej obniżki?
A) o 60% B) o 40% C) o 20% D) o 50%
W wyniku dwóch obniżek cenę komputera obniżono o 40%. Druga z tych obniżek była obniżką o 25%. O ile procent obniżono cenę komputera przy pierwszej obniżce?
A) o 15% B) o 65% C) o 20% D) o 30%
Punkty 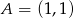 i
i 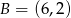 są wierzchołkami trójkąta
są wierzchołkami trójkąta 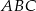 . Wysokości trójkąta
. Wysokości trójkąta 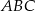 przecinają się w punkcie
przecinają się w punkcie 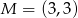 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
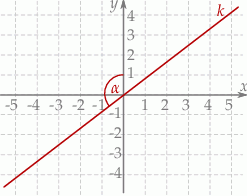
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy 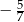 . Wskaż równanie prostej
. Wskaż równanie prostej 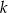 .
.
A) 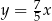 B)
B) 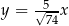 C)
C) 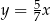 D)
D) 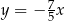
Wyznacz zbiór wartości funkcji
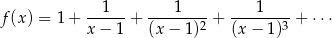
określonej dla wszystkich wartości  , dla których prawa strona powyższego wzoru jest sumą wyrazów zbieżnego szeregu geometrycznego.
, dla których prawa strona powyższego wzoru jest sumą wyrazów zbieżnego szeregu geometrycznego.
Oblicz 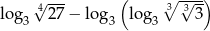 .
.
Oblicz 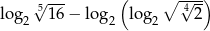 .
.
W ostrosłupie prawidłowym trójkątnym długość krawędzi podstawy jest równa  i jest 4 razy większa niż odległość środka podstawy od ściany bocznej. Oblicz objętość tego ostrosłupa.
i jest 4 razy większa niż odległość środka podstawy od ściany bocznej. Oblicz objętość tego ostrosłupa.
Dany jest wielomian 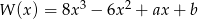 . Jednym pierwiastkiem wielomianu jest prawdopodobieństwo otrzymania co najmniej 2 razy orła w trzykrotnym rzucie monetą. Drugi pierwiastek jest równy prawdopodobieństwu wypadnięcia parzystej liczby oczek na każdej kostce w rzucie dwiema kostkami. Wyznacz trzeci pierwiastek wielomianu.
. Jednym pierwiastkiem wielomianu jest prawdopodobieństwo otrzymania co najmniej 2 razy orła w trzykrotnym rzucie monetą. Drugi pierwiastek jest równy prawdopodobieństwu wypadnięcia parzystej liczby oczek na każdej kostce w rzucie dwiema kostkami. Wyznacz trzeci pierwiastek wielomianu.
Prosta 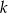 równoległa do osi
równoległa do osi 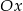 przecina wykres funkcji
przecina wykres funkcji 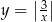 w dwóch punktach
w dwóch punktach 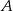 i
i 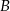 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 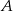 i
i 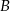 jeżeli wiadomo, że razem z punktem
jeżeli wiadomo, że razem z punktem 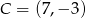 tworzą trójkąt o polu 12.
tworzą trójkąt o polu 12.
Prosta 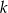 równoległa do osi
równoległa do osi 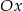 przecina wykres funkcji
przecina wykres funkcji 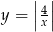 w dwóch punktach
w dwóch punktach 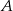 i
i 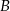 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 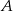 i
i 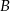 jeżeli wiadomo, że razem z punktem
jeżeli wiadomo, że razem z punktem 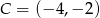 tworzą trójkąt o polu 6.
tworzą trójkąt o polu 6.
Ciąg 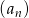 , gdzie
, gdzie 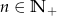 , określony jest następująco:
, określony jest następująco:
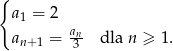
Wyznacz wszystkie wartości 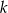 , dla których suma
, dla których suma 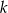 początkowych wyrazów ciągu
początkowych wyrazów ciągu 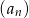 jest większa od
jest większa od 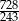 .
.
Ciąg 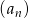 , gdzie
, gdzie 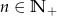 , określony jest następująco:
, określony jest następująco:
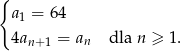
Wyznacz wszystkie wartości 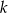 , dla których suma
, dla których suma 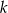 początkowych wyrazów ciągu
początkowych wyrazów ciągu 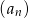 jest równa
jest równa 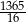 .
.
W tabeli umieszczono wynagrodzenie miesięczne 50 pracowników pewnej firmy:
| Liczba pracowników | 1 | 3 | 4 | 6 | 8 | 12 | 16 |
| Wynagrodzenie | 3600 | 2700 | 2100 | 2000 | 1750 | 1600 | 1450 |
Pracownicy firmy zarabiający mniej niż 2100zł otrzymali podwyżkę w wysokości 500zł, a pracownicy zarabiający powyżej 2000zł – podwyżkę w wysokości 20% średniego wynagrodzenia miesięcznego wszystkich pracowników. Ilu obecnie pracowników tej firmy zarabia więcej niż 3000zł?
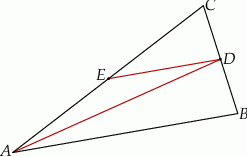
Punkty 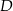 i
i 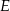 są środkami boków
są środkami boków 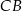 i
i 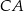 trójkąta
trójkąta 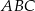 (zobacz rysunek). Wykaż, że odległość punktu
(zobacz rysunek). Wykaż, że odległość punktu 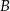 od prostej
od prostej 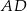 jest dwa razy większa od odległości punktu
jest dwa razy większa od odległości punktu 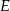 od prostej
od prostej 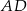 .
.
Znajdź  , dla którego liczby
, dla którego liczby 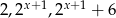 w podanej kolejności tworzą ciąg arytmetyczny.
w podanej kolejności tworzą ciąg arytmetyczny.

