Udowodnij, że w trójkącie prostokątnym dwusieczna kąta prostego dzieli na połowy kąt zawarty między środkową, a wysokością opuszczoną z wierzchołka kąta prostego.
/Szkoła średnia
Liczba 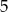 nie należy do dziedziny wyrażenia
nie należy do dziedziny wyrażenia
A) 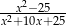 B)
B) 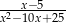 C)
C) 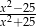 D)
D) 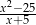
Liczba 4 nie należy do dziedziny wyrażenia
A) 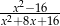 B)
B) 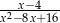 C)
C) 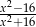 D)
D) 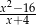
Liczba -5 nie należy do dziedziny wyrażenia
A) 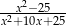 B)
B) 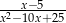 C)
C) 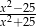 D)
D) 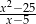
Liczba 3 nie należy do dziedziny wyrażenia
A) 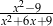 B)
B) 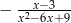 C)
C) 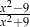 D)
D) 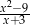
Dla 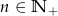 zawsze nieparzysta jest liczba
zawsze nieparzysta jest liczba
A)  B)
B) 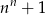 C)
C) 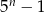 D)
D) 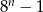
Dla 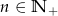 zawsze nieparzysta jest liczba
zawsze nieparzysta jest liczba
A) 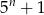 B)
B) 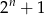 C)
C) 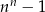 D)
D) 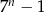
Dla 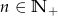 zawsze parzysta jest liczba
zawsze parzysta jest liczba
A) 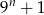 B)
B) 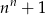 C)
C) 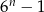 D)
D) 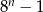
Funkcja 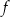 jest określona wzorem
jest określona wzorem 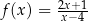 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 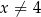 . W kartezjańskim układzie współrzędnych
. W kartezjańskim układzie współrzędnych  punkt
punkt 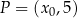 należy do wykresu funkcji
należy do wykresu funkcji 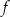 . Oblicz
. Oblicz 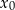 oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji 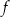 w punkcie
w punkcie 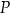 .
.
Średnia arytmetyczna pięciu liczb: 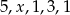 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 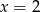 B)
B) 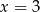 C)
C) 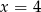 D)
D) 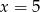
Średnia arytmetyczna pięciu liczb: 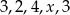 jest równa 3,2. Wtedy
jest równa 3,2. Wtedy
A) 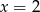 B)
B) 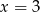 C)
C) 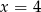 D)
D) 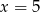
Średnia arytmetyczna siedmiu liczb: 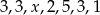 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 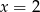 B)
B) 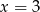 C)
C) 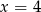 D)
D) 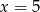
Średnia arytmetyczna dziesięciu liczb 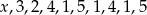 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 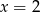 B)
B) 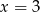 C)
C) 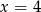 D)
D) 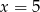
Średnia arytmetyczna pięciu liczb: 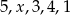 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 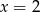 B)
B) 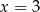 C)
C) 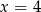 D)
D) 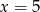
Średnia arytmetyczna zestawu danych: 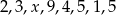 wynosi 4,5. Wynika z tego, że:
wynosi 4,5. Wynika z tego, że:
A) 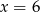 B)
B) 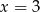 C)
C) 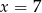 D)
D) 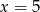
Średnia arytmetyczna ośmiu liczb: 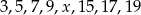 jest równa 11. Wtedy
jest równa 11. Wtedy
A) 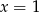 B)
B) 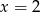 C)
C) 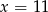 D)
D) 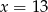
Średnia arytmetyczna pięciu liczb: 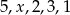 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 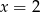 B)
B) 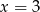 C)
C) 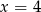 D)
D) 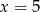
Średnia arytmetyczna sześciu liczb: 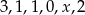 jest równa 2. Wtedy liczba
jest równa 2. Wtedy liczba  jest równa
jest równa
A) 3 B) 4 C) 5 D) 6
Średnia arytmetyczna zestawu danych: 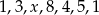 wynosi 4. Wynika z tego, że:
wynosi 4. Wynika z tego, że:
A) 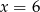 B)
B) 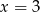 C)
C) 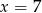 D)
D) 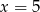
Dla jakiej wartości liczbowej  średnia arytmetyczna liczb:
średnia arytmetyczna liczb: 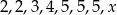 jest równa 4?
jest równa 4?
A) 6 B) 5 C) 4 D) 3
Średnia arytmetyczna zestawu sześciu liczb: 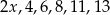 , jest równa 5. Wynika stąd, że
, jest równa 5. Wynika stąd, że
A) 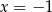 B)
B) 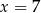 C)
C) 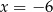 D)
D) 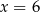
Średnia arytmetyczna liczb 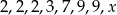 jest równa 4,5. Liczba
jest równa 4,5. Liczba  jest równa
jest równa
A) 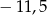 B) 1 C) 1,5 D) 2
B) 1 C) 1,5 D) 2
Średnia arytmetyczna dziesięciu liczb 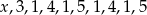 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 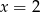 B)
B) 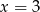 C)
C) 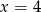 D)
D) 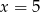
Średnia arytmetyczna liczb: 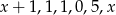 jest równa
jest równa  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A)  B) 2 C)
B) 2 C)  D)
D) 
Średnia arytmetyczna zestawu danych: 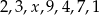 wynosi
wynosi 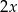 . Wynika z tego, że:
. Wynika z tego, że:
A) 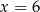 B)
B) 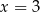 C)
C) 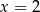 D)
D) 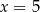
W trójkącie prostokątnym dany jest kąt ostry o mierze  i pole
i pole 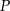 tego trójkąta. Obliczyć długość środkowej poprowadzonej z wierzchołka kąta prostego.
tego trójkąta. Obliczyć długość środkowej poprowadzonej z wierzchołka kąta prostego.
Rowerzysta jedzie ze stałą prędkością 20km/h.
- Napisz wzór wyrażający drogę
 rowerzysty w ciągu
rowerzysty w ciągu 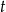 godzin.
godzin. - Sporządź tabelkę wartości
 dla
dla 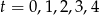 .
. - Naszkicuj wykres zależności
 od
od 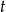 .
.
Wyznacz te wartości parametru 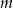 , dla których równanie
, dla których równanie
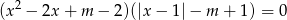
ma dokładnie trzy pierwiastki rzeczywiste? Oblicz te pierwiastki.
Objętość ostrosłupa prawidłowego trójkątnego 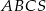 jest równa
jest równa 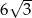 , a krawędź boczna tworzy z płaszczyzną podstawy kąt
, a krawędź boczna tworzy z płaszczyzną podstawy kąt 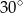 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
Dany jest nieskończony ciąg geometryczny 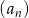 , który zawiera zarówno wyrazy dodatnie, jak i ujemne, w którym
, który zawiera zarówno wyrazy dodatnie, jak i ujemne, w którym 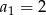 , oraz drugi, czwarty i piąty wyraz są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że suma sześcianów wszystkich wyrazów ciągu
, oraz drugi, czwarty i piąty wyraz są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że suma sześcianów wszystkich wyrazów ciągu 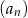 jest równa sumie kwadratów wszystkich wyrazów tego ciągu.
jest równa sumie kwadratów wszystkich wyrazów tego ciągu.
Liczba miejsc zerowych funkcji 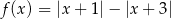 , gdzie
, gdzie 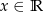 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Funkcja 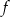 przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb:
przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb: 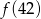 ,
, 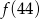 ,
, 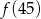 ,
, 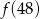 największa to
największa to
A) 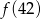 B)
B) 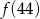 C)
C) 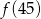 D)
D) 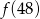
Funkcja 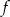 przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb:
przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb: 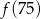 ,
, 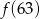 ,
, 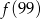 ,
, 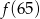 największa to
największa to
A) 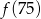 B)
B) 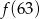 C)
C) 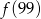 D)
D) 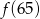
W ciągu arytmetycznym 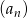 wyraz
wyraz 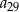 jest dwa razy większy od wyrazu
jest dwa razy większy od wyrazu 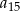 oraz
oraz 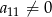 . Wtedy iloraz
. Wtedy iloraz 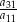 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
W ciągu arytmetycznym 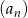 wyraz
wyraz 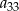 jest dwa razy większy od wyrazu
jest dwa razy większy od wyrazu 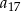 oraz
oraz 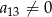 . Wtedy iloraz
. Wtedy iloraz 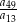 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
Jeżeli 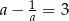 to liczba
to liczba 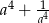 jest równa
jest równa
A) 121 B) 119 C) 123 D) 81
Jeżeli 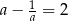 , to liczba
, to liczba 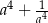 jest równa
jest równa
A) 36 B) 34 C) 6 D) 16
Jeżeli 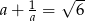 to liczba
to liczba 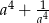 jest równa
jest równa
A) 16 B) 6 C) 14 D) 36
Ze zbioru 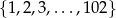 losujemy 2 różne liczby. Jakie jest prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3?
losujemy 2 różne liczby. Jakie jest prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3?
Rozwiąż nierówność 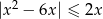 .
.
Pole powierzchni bocznej ostrosłupa prawidłowego trójkątnego równa się 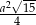 , gdzie
, gdzie  oznacza długość krawędzi podstawy tego ostrosłupa. Zaznacz na poniższym rysunku kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy. Miarę tego kąta oznacz symbolem
oznacza długość krawędzi podstawy tego ostrosłupa. Zaznacz na poniższym rysunku kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy. Miarę tego kąta oznacz symbolem 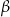 . Oblicz
. Oblicz 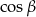 i korzystając z tablic funkcji trygonometrycznych i odczytaj przybliżoną wartość
i korzystając z tablic funkcji trygonometrycznych i odczytaj przybliżoną wartość 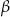 z dokładnością do
z dokładnością do  .
.
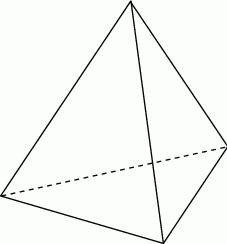
Dany jest ostrosłup prawidłowy czworokątny  o podstawie
o podstawie  . Pole trójkąta
. Pole trójkąta 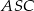 jest równe 120, a cosinus kąta
jest równe 120, a cosinus kąta 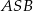 jest równy
jest równy 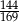 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
W pewnym zakładzie pracy w wyniku dwóch podwyżek zwiększono pensje pracowników o 26%. W ramach pierwszej z tych podwyżek płace zwiększono o 20%. O ile procent zwiększono płace w ramach drugiej podwyżki?
A) o 12% B) o 6% C) o 5% D) o 10%
W wyniku dwóch obniżek cenę komputera obniżono o 40%. Druga z tych obniżek była obniżką o 25%. O ile procent obniżono cenę komputera przy pierwszej obniżce?
A) o 15% B) o 65% C) o 20% D) o 30%
W wyniku dwóch obniżek cenę spodni obniżono o 52%. W ramach pierwszej z tych obniżek cenę zmniejszono o 20%. O ile procent zmniejszono cenę w ramach drugiej obniżki?
A) o 60% B) o 40% C) o 20% D) o 50%
Punkty 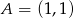 i
i 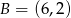 są wierzchołkami trójkąta
są wierzchołkami trójkąta 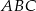 . Wysokości trójkąta
. Wysokości trójkąta 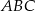 przecinają się w punkcie
przecinają się w punkcie 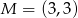 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.

