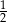Liczba 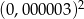 jest równa
jest równa
A) 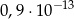 B)
B) 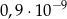 C)
C) 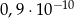 D)
D) 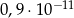
/Szkoła średnia
Liczba 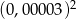 jest równa
jest równa
A) 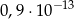 B)
B) 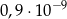 C)
C) 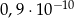 D)
D) 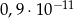
Liczba 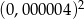 jest równa
jest równa
A) 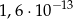 B)
B) 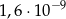 C)
C) 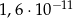 D)
D) 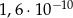
Z punktu 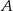 leżącego na okręgu o promieniu
leżącego na okręgu o promieniu 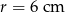 i środku
i środku 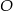 poprowadzono dwie równej długości cięciwy
poprowadzono dwie równej długości cięciwy 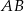 i
i 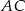 tworzące kąt
tworzące kąt 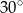 . Oblicz pole czworokąta
. Oblicz pole czworokąta 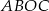 .
.
Kąt  w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek
w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek 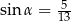 . Bok
. Bok  tego trójkąta ma długość:
tego trójkąta ma długość:
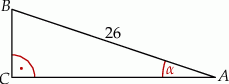
A) 10 B) 24 C) 12 D) 5
Dany jest trójkąt prostokątny o bokach długości 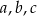 .
.
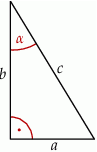
Jeżeli 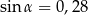 oraz
oraz 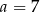 , to
, to
A) 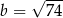 B)
B) 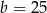 C)
C) 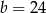 D)
D) 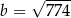
Kąt  w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek
w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek 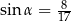 . Bok
. Bok 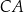 tego trójkąta ma długość:
tego trójkąta ma długość:
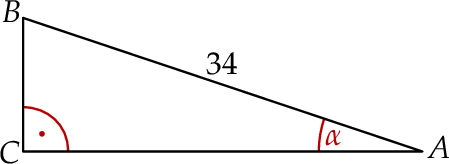
A) 30 B) 8 C) 16 D) 24
Jeśli 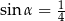 , to długość przyprostokątnej
, to długość przyprostokątnej 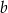 danego trójkąta (patrz rysunek) jest równa
danego trójkąta (patrz rysunek) jest równa
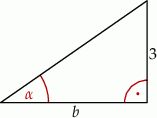
A) 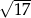 B)
B) 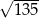 C)
C) 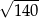 D)
D) 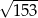
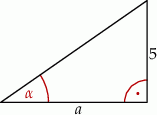
Jeśli 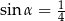 , to długość przyprostokątnej
, to długość przyprostokątnej  danego trójkąta (patrz rysunek) jest równa
danego trójkąta (patrz rysunek) jest równa
A) 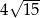 B)
B) 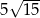 C)
C) 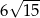 D)
D) 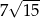
Objętość graniastosłupa prawidłowego czworokątnego jest równa 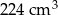 , a promień okręgu opisanego na podstawie ma długość 4 cm. Wyznacz miarę kąta między przekątnymi sąsiednich ścian bocznych wychodzącymi z tego samego wierzchołka graniastosłupa. Wynik podaj z dokładnością do
, a promień okręgu opisanego na podstawie ma długość 4 cm. Wyznacz miarę kąta między przekątnymi sąsiednich ścian bocznych wychodzącymi z tego samego wierzchołka graniastosłupa. Wynik podaj z dokładnością do 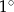 .
.
Rozwiąż równanie 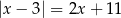 .
.
Wierzchołek 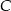 trójkąta
trójkąta 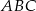 leży na prostej
leży na prostej 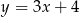 , a pozostałe wierzchołki mają współrzędne
, a pozostałe wierzchołki mają współrzędne 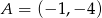 i
i 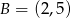 . Uzasadnij, że pole trójkąta
. Uzasadnij, że pole trójkąta 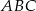 nie zależy od wyboru punktu
nie zależy od wyboru punktu 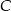 i oblicz to pole.
i oblicz to pole.
Miara kąta między bokiem 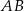 równoległoboku
równoległoboku 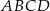 , a przekątną
, a przekątną 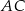 jest równa
jest równa 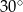 . Długość przekątnej
. Długość przekątnej 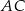 jest równa 5, a długość boku
jest równa 5, a długość boku 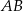 wynosi 4, zatem pole równoległoboku jest równe
wynosi 4, zatem pole równoległoboku jest równe
A) 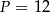 B)
B) 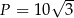 C)
C) 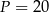 D)
D) 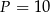
Rzucamy 5 razy symetryczną monetą. Oblicz prawdopodobieństwo otrzymania co najmniej 4 orłów lub co najmniej 4 reszek, jeżeli wiadomo, że otrzymaliśmy co najmniej jedną reszkę.
Dane są dwie bryły: stożek, w którym długość promienia podstawy jest równa 2 dm i wysokość ma długość 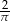 dm oraz ostrosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość 4 dm. Wiedząc, że objętości tych brył są równe, wyznacz kąt nachylenia ściany bocznej ostrosłupa do jego podstawy.
dm oraz ostrosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość 4 dm. Wiedząc, że objętości tych brył są równe, wyznacz kąt nachylenia ściany bocznej ostrosłupa do jego podstawy.
Rozwiąż równanie 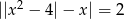 .
.
Na płaszczyźnie dany jest nieskończony ciąg 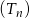 , dla
, dla 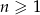 , równoramiennych trójkątów prostokątnych. Pole trójkąta
, równoramiennych trójkątów prostokątnych. Pole trójkąta 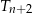 jest dwa razy mniejsze od pola trójkąta
jest dwa razy mniejsze od pola trójkąta 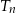 dla
dla 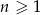 . Uzasadnij, że suma pól trójkątów
. Uzasadnij, że suma pól trójkątów 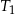 i
i 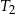 jest równa sumie pól wszystkich pozostałych trójkątów.
jest równa sumie pól wszystkich pozostałych trójkątów.
Na płaszczyźnie dany jest nieskończony ciąg 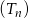 , dla
, dla 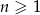 , trójkątów równobocznych. Pole trójkąta
, trójkątów równobocznych. Pole trójkąta 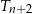 jest dwa razy mniejsze od pola trójkąta
jest dwa razy mniejsze od pola trójkąta 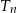 dla
dla 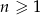 . Uzasadnij, że suma pól trójkątów
. Uzasadnij, że suma pól trójkątów 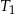 i
i 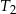 jest równa sumie pól wszystkich pozostałych trójkątów.
jest równa sumie pól wszystkich pozostałych trójkątów.
Rozwiąż nierówność 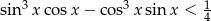 , gdzie
, gdzie 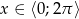 .
.
Wiadomo, że kąt  jest kątem ostrym i
jest kątem ostrym i 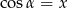 . Wtedy
. Wtedy 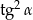 równa się
równa się
A) 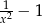 B)
B) 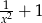 C)
C) 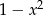 D)
D) 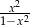
Wiadomo, że kąt  jest kątem ostrym i
jest kątem ostrym i 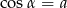 . Wtedy
. Wtedy 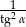 równa się
równa się
A) 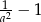 B)
B) 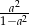 C)
C) 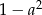 D)
D) 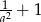
Wiadomo, że kąt  jest kątem ostrym i
jest kątem ostrym i 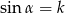 . Wtedy
. Wtedy 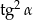 równa się
równa się
A) 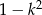 B)
B) 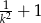 C)
C) 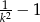 D)
D) 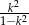
Niech 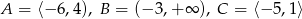 . Wyznacz zbiór
. Wyznacz zbiór 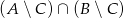 .
.
Wyznacz te wartości parametru 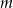 , dla których nierówność
, dla których nierówność 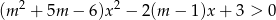 jest prawdziwa dla każdego
jest prawdziwa dla każdego 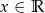 .
.
Wyrażenie 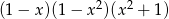 jest równe
jest równe
A) 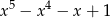 B)
B) 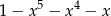 C)
C) 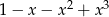 D)
D) 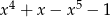
Obwód trójkąta 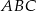 wynosi 28 cm, a jego pole jest równe
wynosi 28 cm, a jego pole jest równe 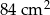 . Promień okręgu wpisanego w trójkąt
. Promień okręgu wpisanego w trójkąt 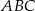 jest równy
jest równy
A) 3 cm B) 6 cm C) 4 cm D) 7 cm
Podaj te wartości  , przy których dla każdego
, przy których dla każdego 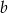 istnieje takie
istnieje takie  , że układ równań:
, że układ równań:
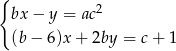
ma zawsze przynajmniej jedno rozwiązanie.
Punkt 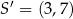 jest obrazem punktu
jest obrazem punktu 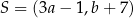 w symetrii osiowej względem osi
w symetrii osiowej względem osi 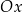 układu współrzędnych, gdy
układu współrzędnych, gdy
A) 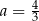 oraz
oraz 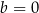 B)
B) 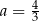 oraz
oraz 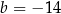
C) 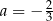 oraz
oraz 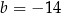 D)
D) 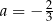 oraz
oraz 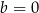
Funkcja kwadratowa 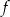 jest określona wzorem
jest określona wzorem 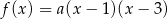 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 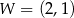 .
.
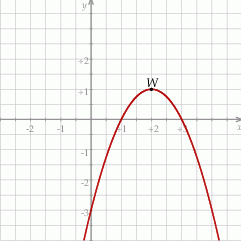
Współczynnik  we wzorze funkcji
we wzorze funkcji 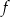 jest równy
jest równy
A) 1 B) 2 C) 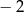 D)
D) 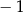
Funkcja kwadratowa 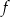 jest określona wzorem
jest określona wzorem 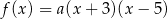 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 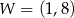 .
.
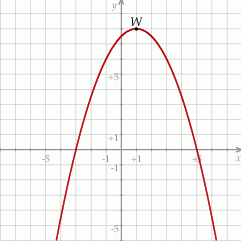
Współczynnik  we wzorze funkcji
we wzorze funkcji 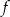 jest równy
jest równy
A) 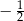 B) 2 C)
B) 2 C) 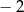 D)
D)