Rozwiąż równanie, w którym lewa strona jest sumą zbieżnego szeregu geometrycznego.
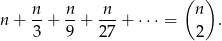
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie, w którym lewa strona jest sumą zbieżnego szeregu geometrycznego.
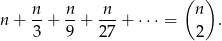
Przekrój osiowy stożka jest trójkątem równoramiennym o ramieniu długości 12. Kąt rozwarcia stożka ma miarę 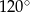 . Objętość stożka wynosi
. Objętość stożka wynosi
A) 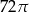 B)
B) 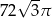 C)
C) 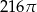 D)
D) 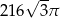
Liczby 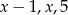 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Rozwiąż równanie 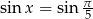 .
.
Rozwiąż równanie 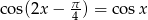 .
.
Wyznacz wszystkie liczby rzeczywiste  , spełniające równanie
, spełniające równanie 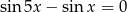 .
.
Rozwiąż równanie 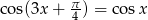 .
.
Rozwiąż równanie 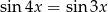 .
.
Rozwiąż równanie 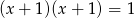 .
.
Rozwiąż równanie kwadratowe 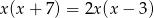 .
.
Rozwiąż równanie 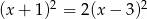 .
.
Rozwiąż równanie 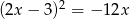 .
.
Rozwiąż równanie 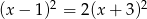 .
.
Rozwiąż równanie 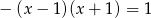 .
.
Dwa okręgi o środkach 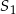 i
i 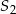 przecinają się w punktach
przecinają się w punktach 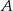 i
i 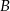 , przy czym punkty
, przy czym punkty 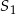 i
i 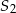 leżą po przeciwnych stronach prostej
leżą po przeciwnych stronach prostej 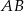 . Miary kątów
. Miary kątów 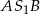 i
i 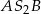 wynoszą odpowiednio
wynoszą odpowiednio 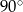 i
i 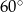 . Wyznacz długości promieni tych okręgów wiedząc, że
. Wyznacz długości promieni tych okręgów wiedząc, że 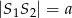 .
.
Kule o jednakowych promieniach ułożono w rzędach tworząc w ten sposób kwadrat. Gdyby usunięto 669 kul, to z pozostałych można by było zbudować trójkąt równoboczny (w pierwszym rzędzie jedna kula, w drugim dwie, w trzecim trzy itd.) Bok trójkąta równobocznego zawierałby wówczas o 8 kul więcej niż bok kwadratu. Z ilu kul zbudowany był kwadrat?
W układzie współrzędnych na płaszczyźnie punkty 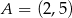 i
i 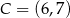 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 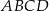 . Wyznacz równanie prostej
. Wyznacz równanie prostej 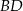 .
.
W układzie współrzędnych na płaszczyźnie punkty 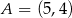 i
i 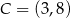 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 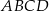 . Wyznacz równanie prostej
. Wyznacz równanie prostej 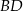 .
.
W kwadracie 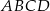 punkty
punkty 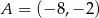 oraz
oraz 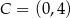 są końcami przekątnej. Wyznacz równanie prostej zawierającej przekątną
są końcami przekątnej. Wyznacz równanie prostej zawierającej przekątną 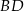 tego kwadratu.
tego kwadratu.
Wiadomo, że 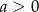 i
i 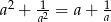 . Wykaż, że
. Wykaż, że 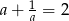 .
.
Do wykresu funkcji nie należy punkt 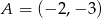 . Funkcja
. Funkcja 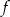 może mieć wzór
może mieć wzór
A) 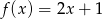 B)
B) 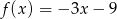 C)
C) 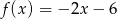 D)
D) 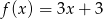
Na podstawie 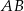 i ramieniu
i ramieniu 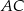 trójkąta równoramiennego
trójkąta równoramiennego 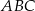 dane są punkty
dane są punkty 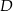 i
i 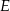 takie, że
takie, że 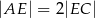 i
i 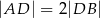 . Punkty
. Punkty 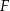 i
i 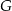 leżą na ramieniu
leżą na ramieniu 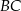 tak, że odcinki
tak, że odcinki 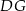 i
i 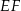 są prostopadłe do prostej
są prostopadłe do prostej 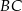 (zobacz rysunek).
(zobacz rysunek).
Pole trójkąta  jest równe 18. Zatem suma pól trójkątów
jest równe 18. Zatem suma pól trójkątów  i
i 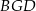 jest równa
jest równa
A) 9 B) 6 C) 3 D) 2
Punkty 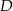 i
i 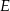 są środkami odpowiednio podstawy
są środkami odpowiednio podstawy 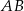 i ramienia
i ramienia 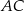 trójkąta równoramiennego
trójkąta równoramiennego 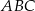 . Punkty
. Punkty 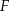 i
i 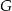 leżą na ramieniu
leżą na ramieniu 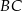 tak, że odcinki
tak, że odcinki 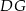 i
i 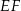 są prostopadłe do prostej
są prostopadłe do prostej 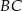 (zobacz rysunek).
(zobacz rysunek).
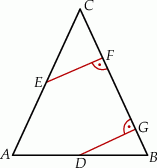
Pole trójkąta  jest równe 2, a pole trójkąta
jest równe 2, a pole trójkąta  jest równe 4. Zatem pole trójkąta
jest równe 4. Zatem pole trójkąta  jest równe
jest równe
A) 24 B) 8 C) 12 D) 16
Długości boków trójkąta są kolejnymi wyrazami ciągu arytmetycznego. Obwód trójkąta jest równy 33, a cosinus największego kąta jest równy  . Oblicz promień okręgu opisanego na tym trójkącie.
. Oblicz promień okręgu opisanego na tym trójkącie.
Prosta 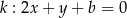 ma dwa punkty wspólne z parabolą
ma dwa punkty wspólne z parabolą 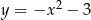 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
A) 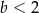 B)
B) 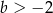 C)
C) 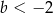 D)
D) 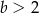
Uzasadnij, że jeżeli  jest liczbą całkowitą to liczba
jest liczbą całkowitą to liczba 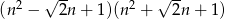 też jest liczbą całkowitą.
też jest liczbą całkowitą.
Wielomiany 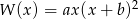 i
i 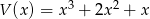 są równe. Oblicz
są równe. Oblicz  i
i 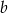 .
.
Rozwiąż nierówność 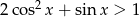 , gdzie
, gdzie 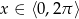 .
.
Jeśli 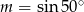 , to
, to
A) 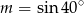 B)
B) 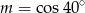 C)
C) 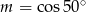 D)
D) 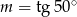
Jeśli 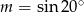 , to
, to
A) 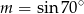 B)
B) 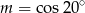 C)
C) 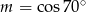 D)
D) 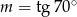
Dwa boki trójkąta wpisanego w okrąg o promieniu 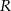 są odpowiednio równe
są odpowiednio równe 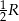 i
i 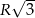 . Oblicz długość trzeciego boku.
. Oblicz długość trzeciego boku.
Punkty 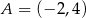 i
i 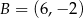 są końcami podstawy trójkąta równoramiennego
są końcami podstawy trójkąta równoramiennego 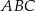 . Prosta zawierająca wysokość
. Prosta zawierająca wysokość 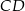 tego trójkąta przecina prostą
tego trójkąta przecina prostą 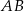 w punkcie
w punkcie
A) 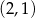 B)
B) 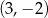 C)
C) 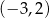 D)
D) 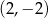
Punkty 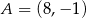 i
i 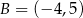 są końcami podstawy trójkąta równoramiennego
są końcami podstawy trójkąta równoramiennego 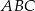 . Prosta zawierająca wysokość
. Prosta zawierająca wysokość 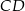 tego trójkąta przecina prostą
tego trójkąta przecina prostą 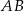 w punkcie
w punkcie
A) 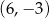 B)
B) 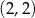 C)
C) 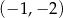 D)
D) 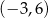
Punkt 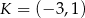 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 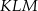 , w którym
, w którym 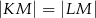 . Odcinek
. Odcinek 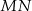 jest wysokością trójkąta i
jest wysokością trójkąta i 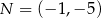 . Zatem
. Zatem
A) 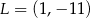 B)
B) 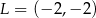 C)
C) 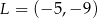 D)
D) 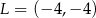
Punkt 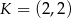 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 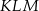 , w którym
, w którym 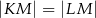 . Odcinek
. Odcinek 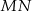 jest wysokością trójkąta i
jest wysokością trójkąta i 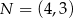 . Zatem
. Zatem
A) 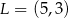 B)
B) 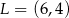 C)
C) 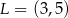 D)
D) 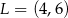
Niech 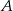 będzie zbiorem wszystkich liczb
będzie zbiorem wszystkich liczb  , które spełniają równość
, które spełniają równość 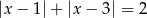 . Niech
. Niech 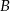 będzie zbiorem wszystkich punktów na osi liczbowej, których suma odległości od punktów 4 i 6 jest niewiększa niż 4. Zaznacz na osi liczbowej zbiory
będzie zbiorem wszystkich punktów na osi liczbowej, których suma odległości od punktów 4 i 6 jest niewiększa niż 4. Zaznacz na osi liczbowej zbiory 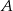 i
i 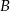 oraz wszystkie punkty, które należą jednocześnie do
oraz wszystkie punkty, które należą jednocześnie do 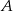 i do
i do 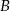 .
.
