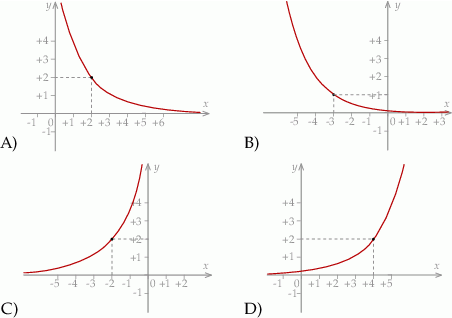
Dane są dwie funkcje określone dla wszystkich liczb rzeczywistych  wzorami
wzorami 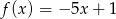 oraz
oraz 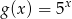 . Liczba punktów wspólnych wykresów tych funkcji jest równa
. Liczba punktów wspólnych wykresów tych funkcji jest równa
A) 3 B) 2 C) 1 D) 0
/Szkoła średnia/Zadania testowe/Funkcje - wykresy/Wykładniczy
Dane są dwie funkcje określone dla wszystkich liczb rzeczywistych  wzorami
wzorami 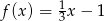 oraz
oraz 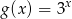 . Liczba punktów wspólnych wykresów tych funkcji jest równa
. Liczba punktów wspólnych wykresów tych funkcji jest równa
A) 3 B) 2 C) 1 D) 0
Dane są dwie funkcje określone dla wszystkich liczb rzeczywistych  wzorami
wzorami 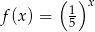 oraz
oraz 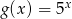 . Liczba punktów wspólnych wykresów tych funkcji jest równa
. Liczba punktów wspólnych wykresów tych funkcji jest równa
A) 0 B) 1 C) 2 D) 3
Wykres funkcji 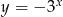 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) I i II B) II i III C) III i IV D) IV i I
Na rysunku przedstawiono fragment wykresu funkcji wykładniczej 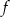 określonej wzorem
określonej wzorem 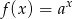 . Punkt
. Punkt 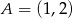 należy do tego wykresu funkcji.
należy do tego wykresu funkcji.
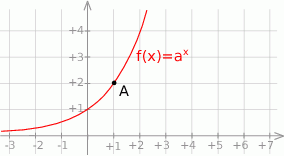
Podstawa  potęgi jest równa
potęgi jest równa
A) 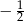 B)
B) 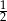 C)
C) 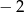 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu funkcji wykładniczej 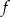 określonej wzorem
określonej wzorem 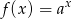 . Punkt
. Punkt 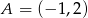 należy do tego wykresu funkcji.
należy do tego wykresu funkcji.
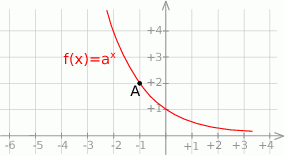
Podstawa  potęgi jest równa
potęgi jest równa
A) 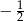 B)
B) 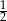 C)
C) 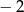 D) 2
D) 2
Funkcja 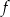 określona jest wzorem
określona jest wzorem 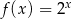 . Funkcja
. Funkcja 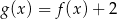 z prostą
z prostą 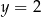
A) ma jeden punkt wspólny B) dwa punkty wspólne
C) nie ma punktów wspólnych D) ma nieskończenie wiele punktów wspólnych
Funkcja 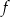 określona jest wzorem
określona jest wzorem 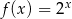 . Wykres funkcji
. Wykres funkcji 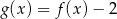 z prostą
z prostą 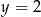
A) ma jeden punkt wspólny B) dwa punkty wspólne
C) nie ma punktów wspólnych D) ma nieskończenie wiele punktów wspólnych
Jeżeli do wykresu funkcji wykładniczej 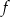 należy punkt
należy punkt 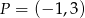 , to funkcja ta określona jest wzorem
, to funkcja ta określona jest wzorem
A) 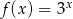 B)
B) 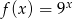 C)
C) 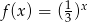 D)
D) 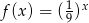
Jeżeli do wykresu funkcji wykładniczej 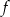 należy punkt
należy punkt 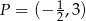 , to funkcja ta określona jest wzorem
, to funkcja ta określona jest wzorem
A) 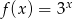 B)
B) 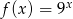 C)
C) 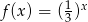 D)
D) 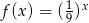
Jeżeli do wykresu funkcji wykładniczej 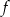 należy punkt
należy punkt 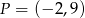 , to funkcja ta określona jest wzorem
, to funkcja ta określona jest wzorem
A) 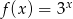 B)
B) 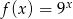 C)
C) 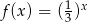 D)
D) 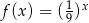
Na rysunku przedstawiono fragment wykresu funkcji wykładniczej 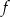 określonej wzorem
określonej wzorem 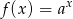 . Wartość funkcji dla
. Wartość funkcji dla 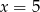 jest cztery razy większa, niż wartość dla
jest cztery razy większa, niż wartość dla 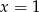 .
.
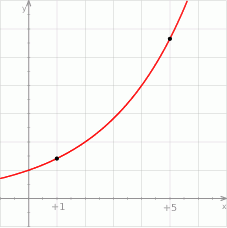
Podstawa  potęgi jest równa
potęgi jest równa
A) 2 B) 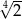 C)
C) 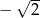 D)
D) 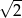
Która z podanych prostych nie przecina wykresu funkcji 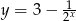 ?
?
A) 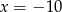 B)
B) 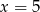 C)
C) 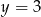 D)
D) 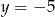
Na rysunku przedstawiono wykres funkcji określonej wzorem
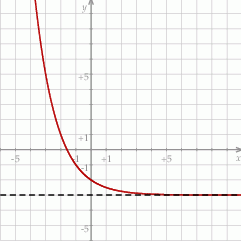
A) 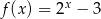 B)
B) 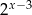 C)
C) 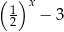 D)
D) 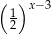
Dana jest funkcja wykładnicza 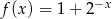 określona dla
określona dla 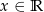 . Zbiorem wartości funkcji
. Zbiorem wartości funkcji 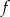 jest przedział
jest przedział
A) 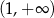 , , | B) 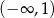 , , |
ponieważ wykres funkcji 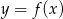 można otrzymać z wykresu funkcji
można otrzymać z wykresu funkcji 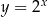 poprzez
poprzez
| 1) | symetrię względem osi 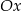 i przesunięcie o 1 jednostkę w dół. i przesunięcie o 1 jednostkę w dół. |
| 2) | symetrię względem osi 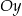 i przesunięcie o 1 jednostkę w górę. i przesunięcie o 1 jednostkę w górę. |
| 3) | symetrię względem osi 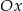 i przesunięcie o 1 jednostkę w górę. i przesunięcie o 1 jednostkę w górę. |
Dane są funkcje 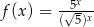 oraz
oraz 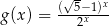 , określone dla wszystkich liczb rzeczywistych
, określone dla wszystkich liczb rzeczywistych  . Punkt wspólny wykresów funkcji
. Punkt wspólny wykresów funkcji 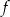 i
i 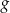
A) nie istnieje B) ma współrzędne 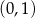
C) ma współrzędne 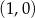 D) ma współrzędne
D) ma współrzędne 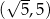
Wykres funkcji 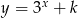 przechodzi przez punkt
przechodzi przez punkt 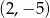 gdy liczba
gdy liczba 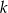 jest równa
jest równa
A) 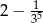 B) 4 C) -14 D) 14
B) 4 C) -14 D) 14
Jeżeli wiadomo, że punkt 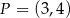 należy do wykresu funkcji
należy do wykresu funkcji 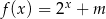 , to
, to
A) 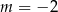 B)
B) 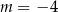 C)
C) 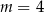 D)
D) 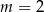
Dana jest funkcja 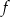 określona wzorem
określona wzorem 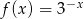 . Wykres funkcji
. Wykres funkcji 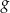 jest symetryczny do wykresu funkcji
jest symetryczny do wykresu funkcji 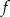 względem osi
względem osi 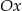 . Zatem
. Zatem
A) 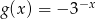 B)
B) 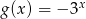 C)
C) 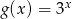 D)
D) 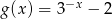
Dana jest funkcja 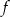 określona wzorem
określona wzorem 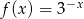 . Wykres funkcji
. Wykres funkcji 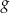 jest symetryczny do wykresu funkcji
jest symetryczny do wykresu funkcji 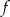 względem osi
względem osi 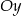 . Zatem
. Zatem
A) 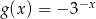 B)
B) 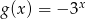 C)
C) 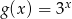 D)
D) 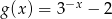
Dana jest funkcja 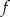 określona wzorem
określona wzorem 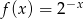 . Wykres funkcji
. Wykres funkcji 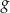 jest symetryczny do wykresu funkcji
jest symetryczny do wykresu funkcji 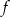 względem osi
względem osi 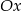 . Zatem
. Zatem
A) 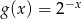 B)
B) 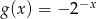 C)
C) 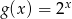 D)
D) 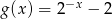
Dane są funkcje 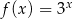 oraz
oraz 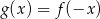 , określone dla wszystkich liczb rzeczywistych
, określone dla wszystkich liczb rzeczywistych  . Punkt wspólny wykresów funkcji
. Punkt wspólny wykresów funkcji 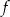 i
i 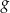
A) nie istnieje B) ma współrzędne 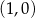
C) ma współrzędne 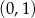 D) ma współrzędne
D) ma współrzędne 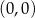
Dane są funkcje 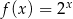 oraz
oraz 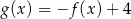 , określone dla wszystkich liczb rzeczywistych
, określone dla wszystkich liczb rzeczywistych  . Punkt wspólny wykresów funkcji
. Punkt wspólny wykresów funkcji 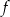 i
i 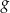
A) nie istnieje B) ma współrzędne 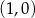
C) ma współrzędne 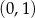 D) ma współrzędne
D) ma współrzędne 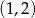
Punkt 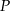 jest punktem wspólnym wykresu funkcji
jest punktem wspólnym wykresu funkcji 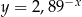 i prostej
i prostej 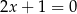 . Odległość punktu
. Odległość punktu 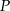 od osi
od osi 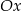 układu współrzędnych jest równa
układu współrzędnych jest równa
A) 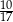 B)
B) 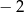 C) 1,7 D) 1
C) 1,7 D) 1
Do wykresu funkcji wykładniczej 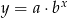 należą punkty
należą punkty 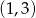 i
i 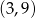 . Zatem liczba
. Zatem liczba 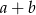 jest równa
jest równa
A) 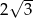 B) 12 C)
B) 12 C) 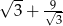 D)
D) 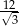
Do wykresu funkcji wykładniczej 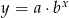 należą punkty
należą punkty 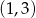 i
i 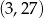 . Zatem liczba
. Zatem liczba 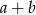 jest równa
jest równa
A) 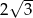 B) 12 C) 4 D)
B) 12 C) 4 D) 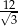
Do wykresu funkcji 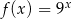 nie należy punkt
nie należy punkt
A) 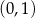 B)
B) 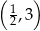 C)
C) 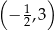 D)
D) 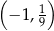
Do wykresu funkcji 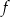 danej wzorem
danej wzorem 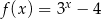 , należy punkt o współrzędnych
, należy punkt o współrzędnych
A) 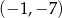 B)
B) 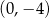 C)
C) 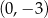 D)
D) 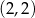
Do wykresu funkcji, określonej dla wszystkich liczb rzeczywistych wzorem 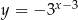 , należy punkt
, należy punkt
A) 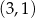 B)
B) 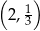 C)
C) 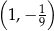 D)
D) 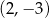
Do wykresu funkcji 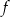 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  wzorem
wzorem 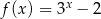 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 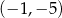 B)
B) 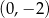 C)
C) 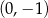 D)
D) 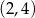
Do wykresu funkcji 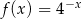 nie należy punkt
nie należy punkt
A) 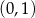 B)
B) 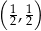 C)
C) 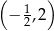 D)
D) 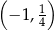
Do wykresu funkcji 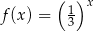 należy punkt
należy punkt
A) 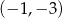 B)
B) 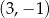 C)
C) 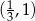 D)
D) 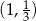
Do wykresu funkcji określonej wzorem 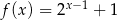 , należy punkt o współrzędnych
, należy punkt o współrzędnych
A) 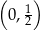 B)
B) 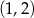 C)
C) 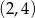 D)
D) 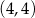
Do wykresu funkcji 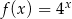 nie należy punkt
nie należy punkt
A) 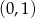 B)
B) 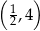 C)
C) 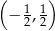 D)
D) 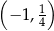
Do wykresu funkcji, określonej dla wszystkich liczb rzeczywistych wzorem 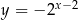 , należy punkt
, należy punkt
A) 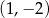 B)
B) 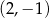 C)
C) 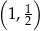 D)
D) 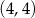
Do wykresu funkcji 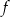 danej wzorem
danej wzorem 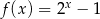 nie należy punkt o współrzędnych
nie należy punkt o współrzędnych
A) 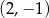 B)
B) 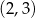 C)
C) 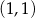 D)
D) 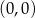
Do wykresu funkcji 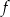 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  wzorem
wzorem 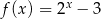 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 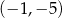 B)
B) 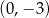 C)
C) 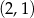 D)
D) 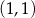
Funkcja 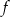 jest określona dla wszystkich liczb rzeczywistych wzorem
jest określona dla wszystkich liczb rzeczywistych wzorem 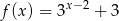 . Prosta
. Prosta 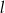 ma równanie
ma równanie 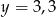 . Ile punktów wspólnych mają wykres funkcji
. Ile punktów wspólnych mają wykres funkcji 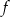 i prosta
i prosta 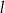 ?
?
A) Zero. B) Jeden. C) Dwa. D) Nieskończenie wiele.
Funkcja 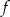 jest określona dla wszystkich liczb rzeczywistych wzorem
jest określona dla wszystkich liczb rzeczywistych wzorem 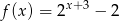 . Prosta
. Prosta 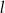 ma równanie
ma równanie 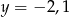 . Ile punktów wspólnych mają wykres funkcji
. Ile punktów wspólnych mają wykres funkcji 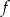 i prosta
i prosta 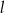 ?
?
A) Zero. B) Jeden. C) Dwa. D) Nieskończenie wiele.
Wykres funkcji 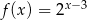 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
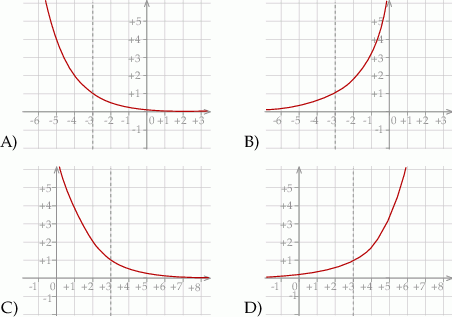
Wykres funkcji 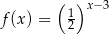 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
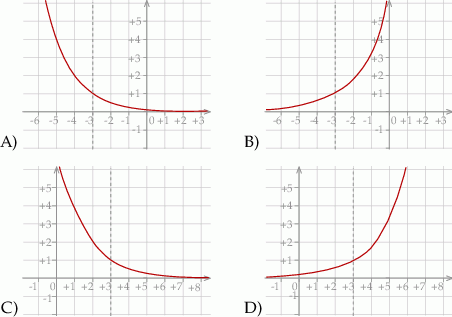
Wykres funkcji 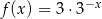 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
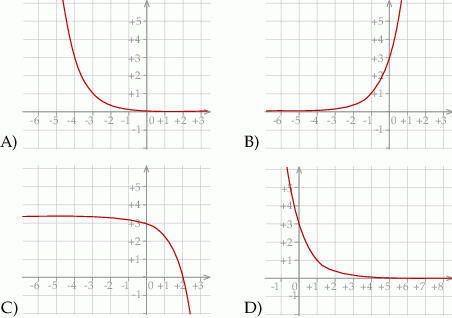
Wykres funkcji 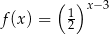 przedstawiony jest na rysunku
przedstawiony jest na rysunku