Reszta z dzielenia wielomianu 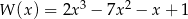 przez dwumian
przez dwumian 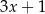 jest równa
jest równa
A) 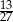 B)
B) 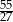 C)
C) 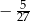 D)
D) 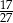
/Szkoła średnia/Zadania testowe/Funkcje/Wielomiany/Dwa wielomiany
Reszta z dzielenia wielomianu 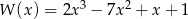 przez dwumian
przez dwumian 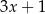 jest równa
jest równa
A) 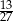 B)
B) 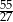 C)
C) 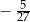 D)
D) 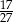
Wielomian 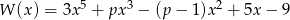 jest podzielny przez dwumian
jest podzielny przez dwumian 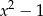 dla
dla 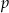 równego
równego
A) 6 B) 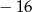 C) 4 D)
C) 4 D) 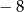
Dane są wielomiany 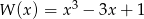 oraz
oraz 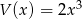 . Wielomian
. Wielomian 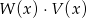 jest równy
jest równy
A) 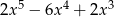 B)
B) 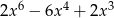 C)
C) 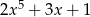 D)
D) 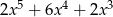
Dane są wielomiany 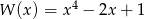 oraz
oraz 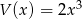 . Wielomian
. Wielomian 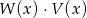 jest równy
jest równy
A) 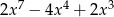 B)
B) 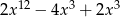 C)
C) 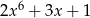 D)
D) 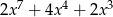
Iloczyn wielomianów 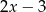 oraz
oraz 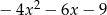 jest równy
jest równy
A) 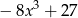 B)
B) 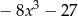 C)
C) 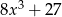 D)
D) 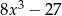
Iloczyn wielomianów 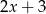 oraz
oraz 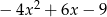 jest równy
jest równy
A) 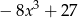 B)
B) 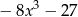 C)
C) 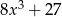 D)
D) 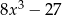
Dane są wielomiany 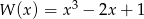 oraz
oraz 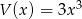 . Wielomian
. Wielomian 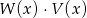 jest równy
jest równy
A) 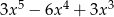 B)
B) 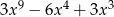 C)
C) 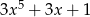 D)
D) 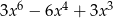
Dane są wielomiany 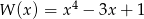 oraz
oraz 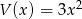 . Wielomian
. Wielomian 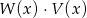 jest równy
jest równy
A) 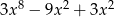 B)
B) 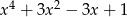 C)
C) 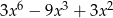 D)
D) 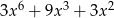
Wielomiany 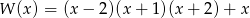 i
i 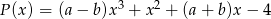 są równe. Z tego wynika, że
są równe. Z tego wynika, że
A) 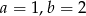 B)
B) 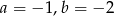 C)
C) 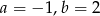 D)
D) 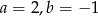
Wielomiany 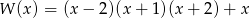 i
i 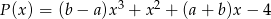 są równe. Z tego wynika, że
są równe. Z tego wynika, że
A) 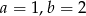 B)
B) 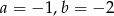 C)
C) 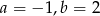 D)
D) 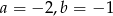
Wielomiany 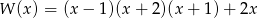 i
i 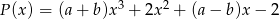 są równe. Z tego wynika, że
są równe. Z tego wynika, że
A) 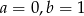 B)
B) 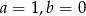 C)
C) 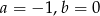 D)
D) 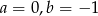
Wielomian 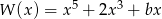 jest podzielny przez wielomian
jest podzielny przez wielomian 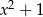 . Wynika stąd, że
. Wynika stąd, że
A) 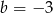 B)
B) 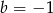 C)
C) 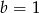 D)
D) 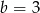
Wielomian 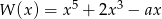 jest podzielny przez wielomian
jest podzielny przez wielomian 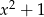 . Wynika stąd, że
. Wynika stąd, że
A) 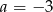 B)
B) 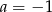 C)
C) 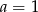 D)
D) 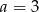
Wielomiany 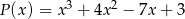 i
i 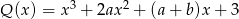 są równe. Zatem
są równe. Zatem
A) 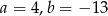 B)
B) 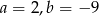 C)
C) 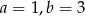 D)
D) 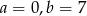
Wielomiany 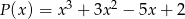 i
i 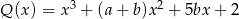 są równe. Zatem
są równe. Zatem
A) 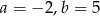 B)
B) 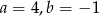 C)
C) 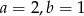 D)
D) 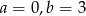
Reszta z dzielenia wielomianu 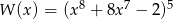 przez dwumian
przez dwumian 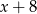 jest równa
jest równa
A) 32 B) 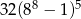 C)
C) 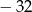 D)
D) 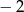
Reszta z dzielenia wielomianu 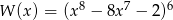 przez dwumian
przez dwumian 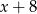 jest równa
jest równa
A) 64 B) 2 C) 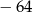 D)
D) 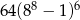
Reszta z dzielenia wielomianu 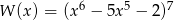 przez dwumian
przez dwumian 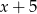 jest równa
jest równa
A) 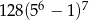 B)
B) 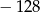 C)
C) 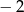 D) 128
D) 128
Reszta z dzielenia wielomianu 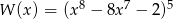 przez dwumian
przez dwumian 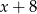 jest równa
jest równa
A) 32 B) 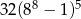 C)
C) 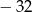 D)
D) 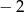
Reszta z dzielenia wielomianu 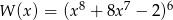 przez dwumian
przez dwumian 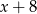 jest równa
jest równa
A) 64 B) 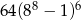 C)
C) 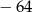 D)
D) 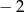
Reszta z dzielenia wielomianu 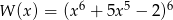 przez dwumian
przez dwumian 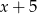 jest równa
jest równa
A) 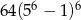 B)
B) 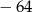 C)
C) 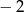 D) 64
D) 64
Reszta z dzielenia wielomianu 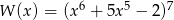 przez dwumian
przez dwumian 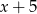 jest równa
jest równa
A) 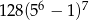 B)
B) 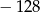 C)
C) 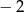 D) 128
D) 128
Iloczyn wielomianów 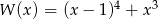 i
i 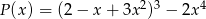 jest wielomianem stopnia
jest wielomianem stopnia
A) 24 B) 10 C) 12 D) 7
Dane są wielomiany 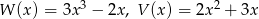 . Stopień wielomianu
. Stopień wielomianu 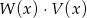 jest równy
jest równy
A) 6 B) 5 C) 4 D) 3
Wielomian 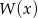 jest iloczynem wielomianów
jest iloczynem wielomianów 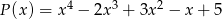 i
i 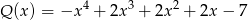 . Zatem stopień wielomianu
. Zatem stopień wielomianu 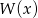 jest równy
jest równy
A) 16 B) 8 C) 4 D) 2
Dane są dwa wielomiany 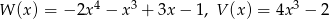 . Stopień wielomianu
. Stopień wielomianu 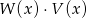 jest równy
jest równy
A) 12 B) 7 C) 4 D) 3
Iloczyn wielomianów 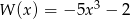 i
i 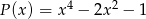 jest wielomianem stopnia
jest wielomianem stopnia
A) 7 B) 3 C) 5 D) 6
Dane są wielomiany: 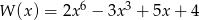 i
i 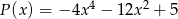 . Stopień wielomianu
. Stopień wielomianu 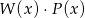 jest równy:
jest równy:
A) 24 B) 10 C) 9 D) 6
Dane są wielomiany: 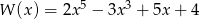 i
i 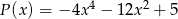 . Stopień wielomianu
. Stopień wielomianu 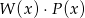 jest równy:
jest równy:
A) 20 B) -8 C) 9 D) 5
Dane są wielomiany 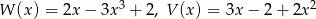 . Stopień wielomianu
. Stopień wielomianu 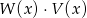 jest równy
jest równy
A) 6 B) 4 C) 5 D) 3
Iloczyn wielomianów 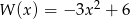 i
i 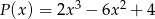 jest wielomianem stopnia
jest wielomianem stopnia
A) 2 B) 3 C) 5 D) 6
Suma dwóch wielomianów, z których każdy jest stopnia piątego, może być wielomianem stopnia
A) drugiego B) szóstego C) dziesiątego D) dwudziestego piątego
Dane są wielomiany 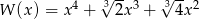 oraz
oraz 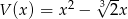 . Wielomian
. Wielomian 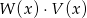 jest równy
jest równy
A) 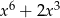 B)
B) 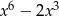 C)
C) 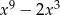 D)
D) 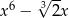
Wielomian 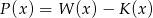 jest siódmego stopnia oraz
jest siódmego stopnia oraz 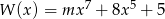 ,
, 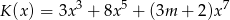 . Wynika stąd, że liczba
. Wynika stąd, że liczba 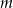 jest różna od
jest różna od
A) 3 B) -1 C) 1 D) 0
Wielomian 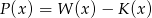 jest siódmego stopnia oraz
jest siódmego stopnia oraz 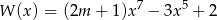 ,
, 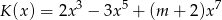 . Wynika stąd, że liczba
. Wynika stąd, że liczba 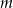 jest różna od
jest różna od
A) 3 B) -1 C) 1 D) 0
Wielomian 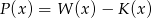 jest piątego stopnia oraz
jest piątego stopnia oraz 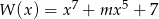 ,
, 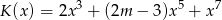 . Wynika stąd, że liczba
. Wynika stąd, że liczba 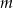 jest różna od
jest różna od
A) 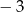 B)
B) 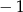 C) 1 D) 3
C) 1 D) 3
Aby otrzymać wielomian 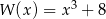 , należy pomnożyć wielomian
, należy pomnożyć wielomian 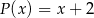 przez wielomian:
przez wielomian:
A) 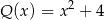 B)
B) 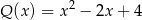
C) 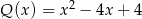 D)
D) 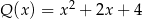
Który z wielomianów należy dodać do wielomianu 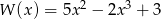 aby otrzymać wielomian
aby otrzymać wielomian 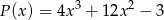 ?
?
A) 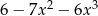 B)
B) 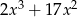 C)
C) 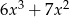 D)
D) 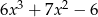
Wielomian 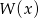 jest sumą wielomianów
jest sumą wielomianów 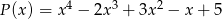 i
i 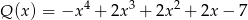 . Zatem stopień wielomianu
. Zatem stopień wielomianu 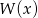 jest równy
jest równy
A) 16 B) 8 C) 4 D) 2
Dane są wielomiany 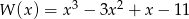 i
i 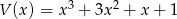 . Stopień wielomianu
. Stopień wielomianu 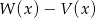 jest równy
jest równy
A) 0 B) 1 C) 2 D) 3
Dane są wielomiany 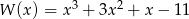 i
i 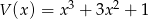 . Stopień wielomianu
. Stopień wielomianu 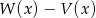 jest równy
jest równy
A) 0 B) 1 C) 2 D) 3
Wielomian 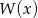 jest sumą wielomianów
jest sumą wielomianów 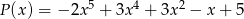 i
i 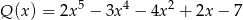 . Zatem stopień wielomianu
. Zatem stopień wielomianu 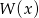 jest równy
jest równy
A) 2 B) 4 C) 5 D) 10
Reszta z dzielenia wielomianu 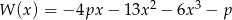 przez dwumian
przez dwumian 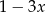 jest równa 3. Zatem
jest równa 3. Zatem
A) 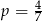 B)
B) 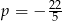 C)
C) 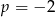 D)
D) 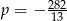
Przez jaki wielomian należy pomnożyć 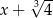 aby otrzymać wielomian
aby otrzymać wielomian 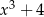 ?
?
A) 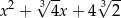 B)
B) 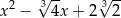
C) 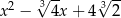 D)
D) 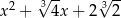
Wielomiany 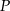 i
i 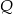 określone są wzorami
określone są wzorami 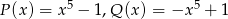 . Wielomian
. Wielomian 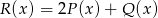 jest stopnia
jest stopnia
A) 0 B) 10 C) 1 D) 5
Wielomiany 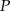 i
i 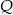 określone są wzorami
określone są wzorami 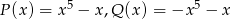 . Wielomian
. Wielomian 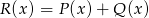 jest stopnia
jest stopnia
A) 0 B) 10 C) 1 D) 5
Wielomiany 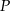 i
i 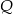 określone są wzorami
określone są wzorami 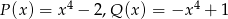 . Wielomian
. Wielomian 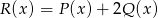 jest stopnia
jest stopnia
A) 0 B) 4 C) 2 D) 8
Funkcje 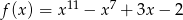 i
i 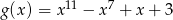 dla argumentu
dla argumentu  przyjmują tę samą wartość. Zatem
przyjmują tę samą wartość. Zatem
A) 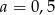 B)
B) 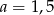 C)
C) 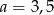 D)
D) 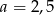
Funkcje 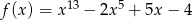 i
i 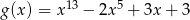 dla argumentu
dla argumentu  przyjmują tę samą wartość. Zatem
przyjmują tę samą wartość. Zatem
A) 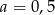 B)
B) 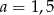 C)
C) 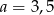 D)
D) 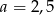
Wielomiany 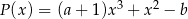 i
i 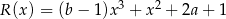 są równe. Zatem liczba
są równe. Zatem liczba 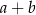
A) należy do zbioru 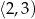 B) jest większa od 3
B) jest większa od 3
C) należy do zbioru 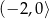 D) jest mniejsza od -2
D) jest mniejsza od -2

