Na bokach 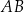 i
i 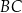 trójkąta
trójkąta 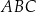 wybrano odpowiednio punkty
wybrano odpowiednio punkty  i
i 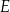 w ten sposób, że
w ten sposób, że 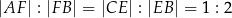 . Odcinki
. Odcinki 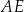 i
i 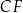 przecinają się w punkcie
przecinają się w punkcie 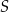 (zobacz rysunek).
(zobacz rysunek).
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 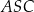 jest podobny do trójkąta jest podobny do trójkąta 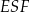 . . | P | F |
Pole trójkąta 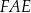 jest równe polu trójkąta jest równe polu trójkąta 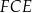 . . | P | F |

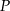 jest punktem wspólnym środkowych
jest punktem wspólnym środkowych 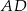 i
i 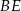 w trójkącie
w trójkącie 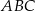 . Wówczas odcinki
. Wówczas odcinki 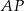 i
i 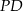 mogą mieć długości
mogą mieć długości 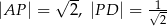
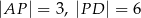
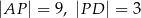
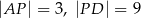
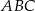 mają długości
mają długości 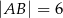 i
i 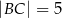 . Sinus największego kąta tego trójkąta jest równy
. Sinus największego kąta tego trójkąta jest równy  . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe. 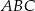 jest mniejsze od 10.
jest mniejsze od 10. 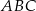 trójkąta
trójkąta 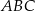 jest równy
jest równy 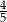 .
.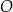 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 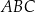 oraz
oraz  ,
,  . Prosta
. Prosta  przecina bok
przecina bok 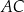 trójkąta
trójkąta 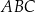 w punkcie
w punkcie 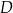 (zobacz rysunek).
(zobacz rysunek). 
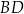 i
i 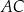 są prostopadłe.
są prostopadłe. 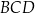 i
i 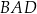 jest równy 0,9.
jest równy 0,9.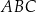 długość podstawy
długość podstawy 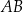 jest równa 4, a długość ramienia
jest równa 4, a długość ramienia 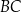 jest równa 6. Dwusieczna kąta
jest równa 6. Dwusieczna kąta 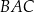 przecina bok
przecina bok 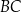 w punkcie
w punkcie 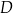 .
. 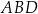 jest prostokątny.
jest prostokątny. 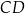 jest krótszy od odcinka
jest krótszy od odcinka 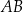 .
.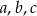 . Stosunek
. Stosunek 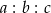 jest równy 3:5:7. Które zdanie jest fałszywe?
jest równy 3:5:7. Które zdanie jest fałszywe? jest o 12,5% mniejsza od liczby
jest o 12,5% mniejsza od liczby 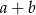
 stanowi 20% liczby
stanowi 20% liczby 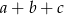
 stanowi 25% liczby
stanowi 25% liczby 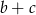
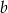 to 60% liczby
to 60% liczby  .
.  długość boku
długość boku 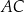 jest równa 3, a długość boku
jest równa 3, a długość boku 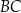 jest równa 4. Dwusieczna kąta
jest równa 4. Dwusieczna kąta 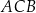 przecina bok
przecina bok 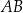 w punkcie
w punkcie 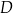 . Stosunek
. Stosunek 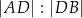 jest równy
jest równy 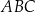 długość boku
długość boku 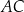 jest równa 6, a długość boku
jest równa 6, a długość boku 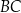 jest równa 8. Dwusieczna kąta
jest równa 8. Dwusieczna kąta 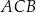 przecina bok
przecina bok 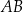 w punkcie
w punkcie 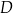 . Stosunek
. Stosunek 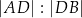 jest równy
jest równy 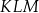 , w którym
, w którym 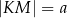 ,
, 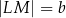 oraz
oraz 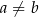 . Dwusieczna kąta
. Dwusieczna kąta 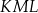 przecina bok
przecina bok 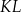 w punkcie
w punkcie 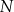 takim, że
takim, że 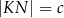 ,
, 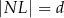 oraz
oraz 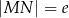 (zobacz rysunek).
(zobacz rysunek). 
 prawdziwa jest równość
prawdziwa jest równość 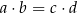
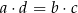
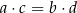
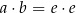
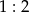 .
. 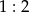 .
. 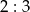 .
. 