Wyrażenie 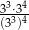 ma wartość
ma wartość
A) 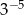 B)
B) 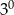 C)
C) 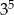 D)
D) 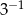
/Szkoła podstawowa/Zadania testowe
Wyrażenie 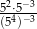 ma wartość
ma wartość
A) 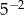 B)
B) 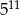 C)
C) 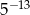 D)
D) 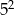
Która równość jest fałszywa?
A) 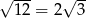 B)
B) 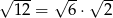 C)
C) 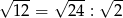 D)
D) 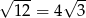
Która równość jest fałszywa?
A) 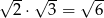 B)
B) 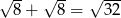 C)
C) 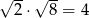 D)
D) 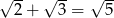
Jeśli 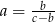 , to
, to
A) 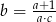 B)
B) 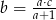 C)
C) 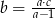 D)
D) 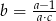
Jeśli 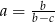 , to
, to
A) 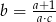 B)
B) 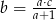 C)
C) 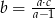 D)
D) 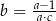
Dane są liczby 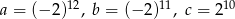 .
.
Liczby te uporządkowane od najmniejszej do największej to:
A) 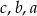 B)
B) 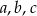 C)
C) 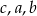 D)
D) 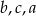
Dane są liczby 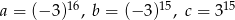 .
.
Liczby te uporządkowane od największej do najmniejszej to:
A) 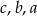 B)
B) 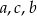 C)
C) 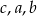 D)
D) 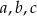
Oprocentowanie kredytu konsumpcyjnego wynosiło w marcu 16%. W kwietniu wzrosło o 25%. O ile punktów procentowych zwiększyło się oprocentowanie kredytu?
A) o 4 B) o 9 C) o 25 D) o 41
Oprocentowanie kredytu konsumpcyjnego wynosiło w marcu 15%. W kwietniu wzrosło o 30%. O ile punktów procentowych zwiększyło się oprocentowanie kredytu?
A) o 45 B) o 30 C) o 15 D) o 4,5
Oprocentowanie kredytu konsumpcyjnego wynosiło w marcu 20%. W kwietniu wzrosło o 20%. O ile punktów procentowych zwiększyło się oprocentowanie kredytu?
A) o 0 B) o 20 C) o 4 D) o 40
Na przekątnej 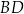 kwadratu
kwadratu 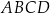 o boku długości 4 zbudowano trójkąt równoboczny
o boku długości 4 zbudowano trójkąt równoboczny 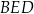 .
.
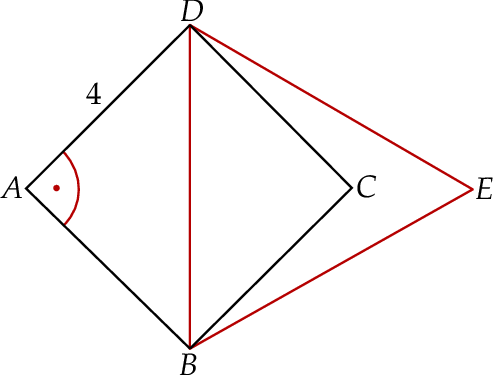
Pole trójkąta 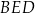 jest równe
jest równe
A) 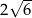 B)
B) 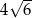 C)
C) 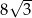 D)
D) 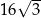
Na poniższym wykresie przedstawiono jak zmieniała się liczba ludności Europy i Afryki w latach 1950–2010 (wykresy mają różne osie pionowe).
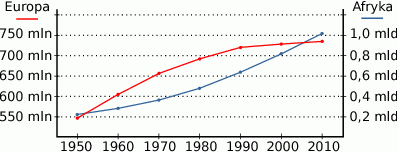
Wskaż zdanie prawdziwe.
A) W roku 2000 Europa liczyła więcej mieszkańców niż Afryka
B) W 1990 roku w Afryce mieszkało około 600 mln ludzi
C) W całym przedstawionym okresie w Europie mieszkało mniej osób niż w Afryce
D) W latach 1950-2010 liczba mieszkańców Afryki podwoiła się
Zosia zebrała 2 kg malin i wsypała je do trzech takich samych pojemników. Masa pustego pojemnika była równa 0,05 kg. Pierwszy pojemnik z malinami miał masę 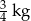 , a masa drugiego pojemnika z malinami była równa 0,70 kg. Ile malin wsypała Zosia do trzeciego pojemnika?
, a masa drugiego pojemnika z malinami była równa 0,70 kg. Ile malin wsypała Zosia do trzeciego pojemnika?
A) 0,45 kg B) 0,55 kg C) 0,60 kg D) 0,65 kg
Na rysunku przedstawiono fragment siatki ostrosłupa prawidłowego czworokątnego.
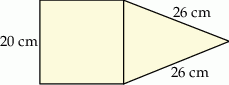
Suma długości krawędzi bocznych tego ostrosłupa jest równa A/B.
A) 360 cm B) 104 cm
Pole powierzchni całkowitej tego ostrosłupa jest równa C/D.
C) 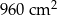 D)
D) 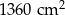
W klasie jest o 25% więcej chłopców niż dziewcząt. Jaką część wszystkich uczniów tej klasy stanowią chłopcy?
A) 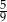 B)
B) 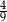 C)
C) 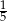 D)
D) 
W klasie jest o 15% więcej chłopców niż dziewcząt. Jaką część wszystkich uczniów tej klasy stanowią chłopcy?
A) 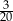 B)
B) 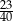 C)
C) 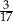 D)
D) 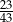
Dziewczęta stanowią 30% uczniów w pewnej klasy. Wynika stąd, że chłopcy stanowią
A) 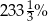 liczby dziewcząt B)
liczby dziewcząt B) 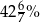 liczby dziewcząt
liczby dziewcząt
C) 21% liczby dziewcząt D) 70% liczby dziewcząt
Chłopcy stanowią 25% uczniów w pewnej klasy. Wynika stąd, że dziewczęta stanowią
A) 175% liczby chłopców B) 200% liczby chłopców
C) 75% liczby chłopców D) 300% liczby chłopców
Dziewczęta stanowią 40% uczniów w pewnej klasy. Wynika stąd, że chłopcy stanowią
A) 50% liczby dziewcząt B) 150% liczby dziewcząt
C) 60% liczby dziewcząt D) 120% liczby dziewcząt
W układzie współrzędnych zaznaczono trzy kolejne wierzchołki równoległoboku.
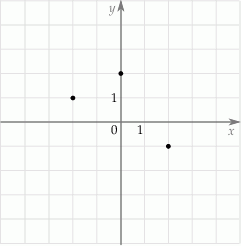
Który z punktów nie może być czwartym wierzchołkiem tego równoległoboku?
A) 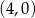 B)
B) 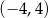 C)
C) 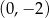 D)
D) 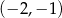
W pudełku są trzy rodzaje piłek: czerwone, niebieskie i zielone. Czerwonych piłek jest trzy razy więcej niż niebieskich, a zielonych jest dwa razy mniej niż czerwonych. Losujemy jedną piłkę. Prawdopodobieństwo, że wylosujemy piłkę zieloną, jest równe
A) 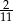 B)
B) 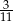 C)
C) 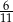 D)
D) 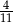
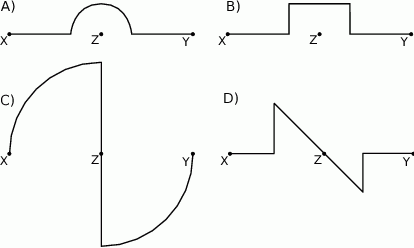
Piechur szedł z punktu 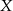 do punktu
do punktu 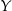 ze stałą prędkością. Na wykresie poniżej zilustrowano, jak zmieniała się odległość piechura od punktu
ze stałą prędkością. Na wykresie poniżej zilustrowano, jak zmieniała się odległość piechura od punktu 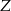 .
.
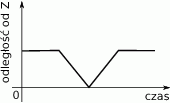
Na którym z poniższych rysunków zilustrowano, jak mogła wyglądać trasa piechura pomiędzy punktami 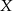 i
i 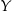 ?
?
Maturzysta na rozwiązanie testu składającego się z 34 zadań przeznaczył 169 minut, przy czym na rozwiązanie każdego z 9 zadań otwartych przeznaczył trzy razy więcej czasu niż na rozwiązanie każdego z zdań zamkniętych. Średnia liczba sekund przeznaczonych na jedno zadanie zamknięte jest równa
A) 180 B) 205 C) 195 D) 170
Dane są trzy wyrażenia:
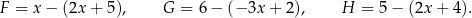
Dla każdej wartości  prawdziwa jest równość
prawdziwa jest równość
A) 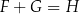 B)
B) 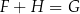 C)
C) 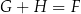 D)
D) 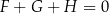
Dane są dwie liczby  i
i 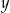 . Wiadomo, że
. Wiadomo, że 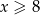 oraz
oraz 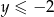 .
.
![]()
Najmniejsza możliwa wartość różnicy 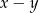 jest równa:
jest równa:
A) 10 B) 6 C) 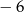 D)
D) 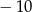
Dane są dwie liczby  i
i 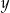 . Wiadomo, że
. Wiadomo, że 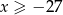 oraz
oraz 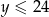 .
.
![]()
Największa możliwa wartość różnicy 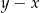 jest równa:
jest równa:
A) 0 B) 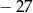 C) 51 D) 24
C) 51 D) 24
Dane są dwie liczby  i
i 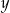 . Wiadomo, że
. Wiadomo, że 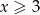 oraz
oraz 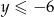 .
.
![]()
Najmniejsza możliwa wartość różnicy 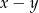 jest równa:
jest równa:
A) 3 B) 9 C) 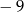 D)
D) 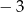
Dana jest liczba 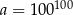 . Liczba
. Liczba 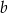 stanowi 1% liczby
stanowi 1% liczby  . Wówczas
. Wówczas
A) 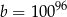 B)
B) 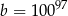 C)
C) 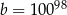 D)
D) 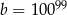
Płyta kosztowała 80 zł, a po obniżce 60 zł. O ile procent obniżono cenę płyty?
A) 20% B) 25% C) 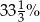 D) 75%
D) 75%
Książka kosztowała 75 zł, a po obniżce 60 zł. O ile procent obniżono cenę książki?
A) 20% B) 25% C) 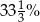 D) 75%
D) 75%
Odtwarzacz kosztujący 340 zł sprzedano podczas wyprzedaży za 255 zł. Obniżka wynosiła
A) 15% B) 20% C) 40% D) 25%
Buty, które kosztowały 220 złotych, przeceniono i sprzedano za 176 złotych. O ile procent obniżono cenę butów?
A) 80 B) 20 C) 22 D) 44
W ramach wyprzedaży sezonowej płaszcz o początkowej wartości 240 zł przeceniono na 200 zł. Zatem cenę tego płaszcza obniżono o
A) 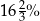 jego początkowej wartości.
jego początkowej wartości.
B) 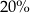 jego początkowej wartości.
jego początkowej wartości.
C) 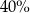 jego początkowej wartości.
jego początkowej wartości.
D) 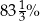 jego początkowej wartości.
jego początkowej wartości.
Rower kosztujący 270 zł sprzedano podczas wyprzedaży za 216 zł. Obniżka wynosiła
A) 15% B) 20% C) 40% D) 80%
Kurtkę, która kosztowała 450 złotych, przeceniono i sprzedano za 387 złotych. O ile procent obniżono cenę kurtki?
A) 14 B) 15 C) 20 D) 24
Narty kosztowały 680 zł. O ile procent należałoby obniżyć cenę nart, aby kosztowały 595 zł?
A) 8,5% B) 12,5% C) 14,2% D) 25%
Kąty 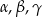 pewnego trójkąta spełniają dwa warunki:
pewnego trójkąta spełniają dwa warunki: 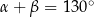 i
i 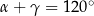 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt  ma miarę ma miarę 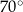 . . | P | F |
Różnica miar między kątem największym a kątem najmniejszym w tym trójkącie jest równa 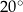 . . | P | F |

