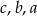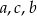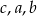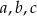Suma siedemdziesięciu czterech liczb dodatnich jest równa 1978. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Po zmniejszeniu każdej z tych liczb o 6 suma otrzymanych liczb będzie równa 1536. | P | F |
| Po zwiększeniu każdej z tych liczb o 50% suma otrzymanych liczb będzie równa 2967. | P | F |

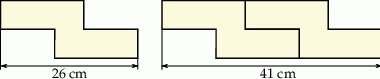

 ma długość
ma długość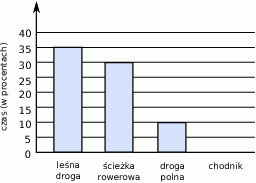
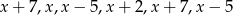 jest równa średniej tych liczb. Zatem liczba
jest równa średniej tych liczb. Zatem liczba 
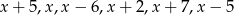 jest dwa razy większa od średniej tych liczb. Zatem liczba
jest dwa razy większa od średniej tych liczb. Zatem liczba 
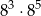
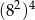
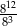
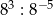

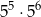
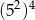
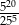
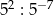

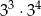
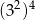
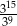
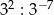



 całej kwoty, w drugim tygodniu
całej kwoty, w drugim tygodniu 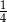 pozostałej kwoty, w trzecim tygodniu wydał dwa razy więcej pieniędzy niż w drugim tygodniu. W czwartym tygodniu wydał pozostałe 75 zł. Jeżeli przez
pozostałej kwoty, w trzecim tygodniu wydał dwa razy więcej pieniędzy niż w drugim tygodniu. W czwartym tygodniu wydał pozostałe 75 zł. Jeżeli przez  oznaczymy kwotę kieszonkowego, którą otrzymał Jacek, to sytuację przedstawioną w zadaniu opisuje równanie
oznaczymy kwotę kieszonkowego, którą otrzymał Jacek, to sytuację przedstawioną w zadaniu opisuje równanie 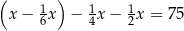
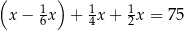
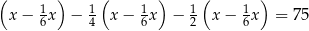
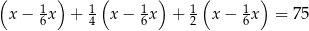
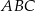 , w którym
, w którym 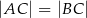 i
i 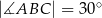 poprowadzono wysokość
poprowadzono wysokość 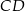 i dwusieczną kąta
i dwusieczną kąta 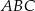 przecinającą bok
przecinającą bok 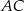 w punkcie
w punkcie 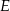 . Wysokość i dwusieczna przecinają się w punkcie
. Wysokość i dwusieczna przecinają się w punkcie 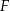 .
. 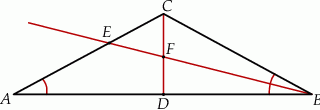
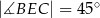
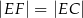
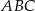 , w którym
, w którym 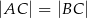 i
i 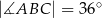 poprowadzono wysokość
poprowadzono wysokość 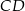 i dwusieczną kąta
i dwusieczną kąta 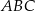 przecinającą bok
przecinającą bok 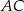 w punkcie
w punkcie 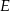 . Wysokość i dwusieczna przecinają się w punkcie
. Wysokość i dwusieczna przecinają się w punkcie 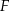 .
. 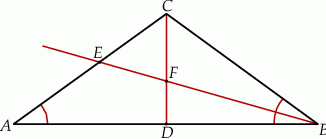
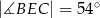
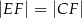
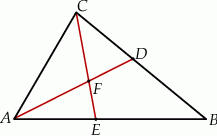
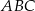 , w którym
, w którym 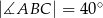 ,
, 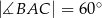 poprowadzono dwusieczne
poprowadzono dwusieczne 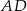 i
i 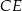 , które przecinają się w punkcie
, które przecinają się w punkcie 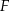 .
. 
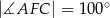
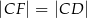
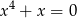
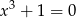
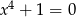
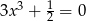
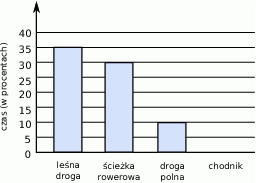
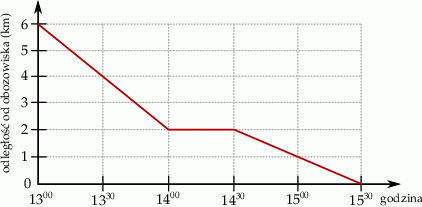
 glazurnik rozpoczął godzinną przerwę.
glazurnik rozpoczął godzinną przerwę. 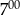 do
do 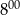 glazurnik ułożył mniej płytek niż od
glazurnik ułożył mniej płytek niż od 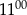 do
do 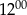 .
. 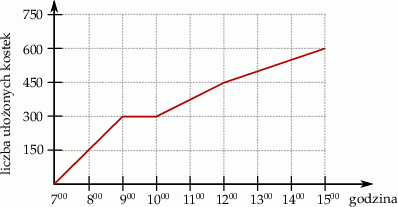
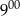 brukarz rozpoczął godzinną przerwę.
brukarz rozpoczął godzinną przerwę. 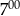 do
do 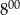 brukarz ułożył więcej kostek niż od
brukarz ułożył więcej kostek niż od 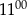 do
do  .
. 
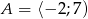 . Liczb pierwszych, które należą do tego zbioru jest
. Liczb pierwszych, które należą do tego zbioru jest 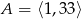 . Liczb pierwszych, które należą do tego zbioru jest
. Liczb pierwszych, które należą do tego zbioru jest 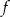 jest określona wzorem
jest określona wzorem 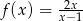 dla
dla 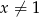 . Wartość funkcji
. Wartość funkcji 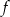 dla argumentu
dla argumentu 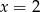 jest równa
jest równa 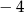
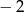
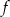 jest określona wzorem
jest określona wzorem 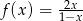 dla
dla 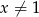 . Wartość funkcji
. Wartość funkcji 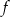 dla argumentu
dla argumentu 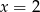 jest równa
jest równa 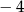
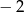
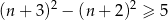
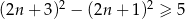
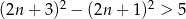
![2 [(2n + 3) − (2n + 1 )] ≥ 5](https://img.zadania.info/zad/3694791/HzadT3x.gif)
![[(n + 3) − (n + 2)]2 ≥ 5](https://img.zadania.info/zad/5555770/HzadT0x.gif)
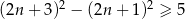
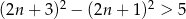
![2 [(2n + 3) − (2n + 1 )] ≥ 5](https://img.zadania.info/zad/5555770/HzadT3x.gif)
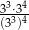 ma wartość
ma wartość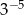
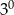
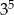
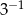
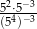 ma wartość
ma wartość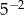
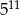
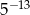
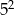
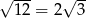
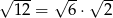
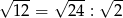
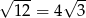
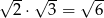
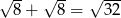
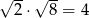
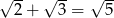
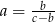 , to
, to 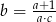
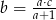
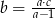
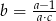
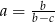 , to
, to 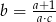
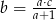
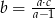
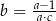
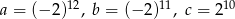 .
. 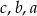
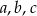
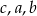
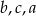
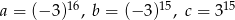 .
.