Kasia ma 6 lat. Średnia arytmetyczna wieku Ani i Pawła jest równa 12 lat. Średnia arytmetyczna wieku Kasi, Ani i Pawła jest równa
A) 6 lat B) 9 lat C) 10 lat D) 15 lat
/Szkoła podstawowa/Zadania testowe
Ola ma 7 lat. Średnia arytmetyczna wieku Ewy i Karola jest równa 10 lat. Średnia arytmetyczna wieku Oli, Ewy i Karola jest równa
A) 6 lat B) 9 lat C) 10 lat D) 15 lat
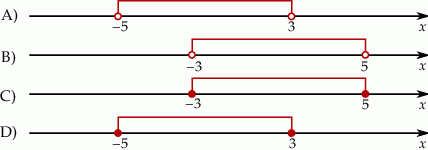
Wskaż rysunek, na którym przedstawiono przedział, będący zbiorem wszystkich rozwiązań nierówności 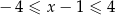 .
.
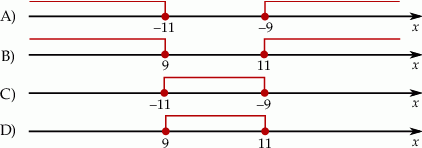
Wskaż rysunek, na którym jest przedstawiony zbiór wszystkich liczb  spełniających warunek:
spełniających warunek: 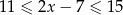 .
.
Rozwiązaniem nierówności 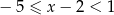 jest zbiór
jest zbiór
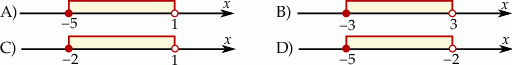
Wskaż rysunek, na którym przedstawiono przedział, będący zbiorem wszystkich rozwiązań nierówności 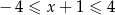 .
.
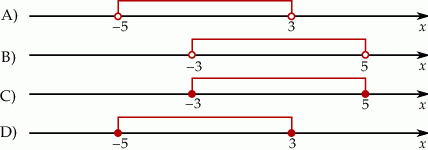
Rozwiązaniem nierówności 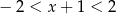 jest zbiór liczb
jest zbiór liczb
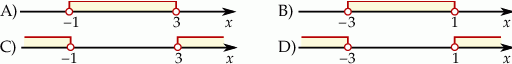
Rozwiązaniem nierówności 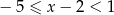 jest zbiór
jest zbiór
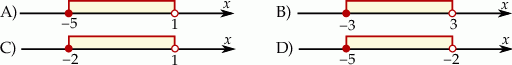
Rozwiązaniem nierówności 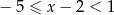 jest zbiór
jest zbiór
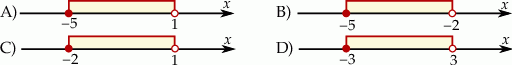
Wskaż rysunek, na którym jest przedstawiony zbiór wszystkich liczb  spełniających warunek:
spełniających warunek: 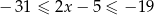 .
.
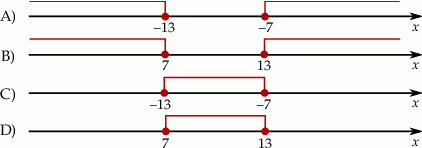
Kulki magnetyczne są sprzedawane w zestawach w kształcie sześcianu o krawędzi składającej się z 6 kulek (zobacz rysunek).

Kamil kupił 3 takie zestawy kulek magnetycznych, a następnie zbudował z nich wszystkich pewną liczbę sześcianów o krawędzi składającej się z 3 kulek.
Kamil kupił w sumie A/B kulek magnetycznych.
A) 648 B) 216
Kamil zbudował C/D sześciany o krawędzi składającej się z 3 kulek.
C) 24 D) 72
Suma liczby  i
i 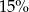 tej liczby jest równa 230. Równaniem opisującym tę zależność jest
tej liczby jest równa 230. Równaniem opisującym tę zależność jest
A) 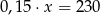 B)
B) 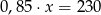 C)
C) 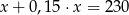 D)
D) 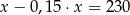
Różnica liczby  i
i 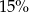 tej liczby jest równa 255. Równaniem opisującym tę zależność jest
tej liczby jest równa 255. Równaniem opisującym tę zależność jest
A) 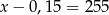 B)
B) 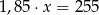 C)
C) 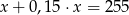 D)
D) 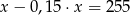
Cztery pompy o jednakowej wydajności pracując jednocześnie, wypompowały wodę zgromadzoną w zbiorniku w czasie 12 godzin.
Ile takich pomp należałoby użyć, aby tę samą ilość wody wypompować w ciągu 6 godzin?
A) 2 B) 3 C) 6 D) 8
Trzy pompy o jednakowej wydajności pracując jednocześnie, wypompowały wodę zgromadzoną w zbiorniku w czasie 24 godzin.
Ile takich pomp należałoby użyć, aby tę samą ilość wody wypompować w ciągu 8 godzin?
A) 9 B) 8 C) 6 D) 12
Na rysunku przedstawiono prostokąt. Długość dłuższego boku oznaczono symbolem  oraz opisano za pomocą wyrażenia algebraicznego
oraz opisano za pomocą wyrażenia algebraicznego 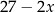 . Długość krótszego boku oznaczono symbolem
. Długość krótszego boku oznaczono symbolem 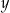 oraz opisano za pomocą wyrażenia algebraicznego
oraz opisano za pomocą wyrażenia algebraicznego 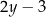 .
.
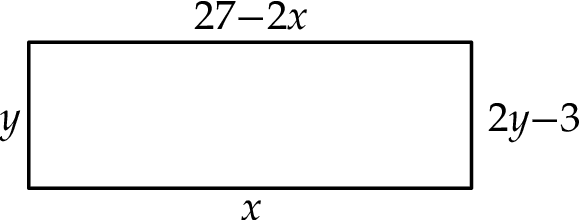
Które równanie nie opisuje poprawnej zależności między wartościami  i
i 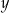 ?
?
A) 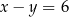 B)
B) 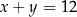 C)
C) 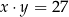 D)
D) 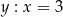
Na rysunku przedstawiono prostokąt. Długość dłuższego boku oznaczono symbolem  oraz opisano za pomocą wyrażenia algebraicznego
oraz opisano za pomocą wyrażenia algebraicznego 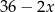 . Długość krótszego boku oznaczono symbolem
. Długość krótszego boku oznaczono symbolem 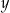 oraz opisano za pomocą wyrażenia algebraicznego
oraz opisano za pomocą wyrażenia algebraicznego 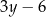 .
.
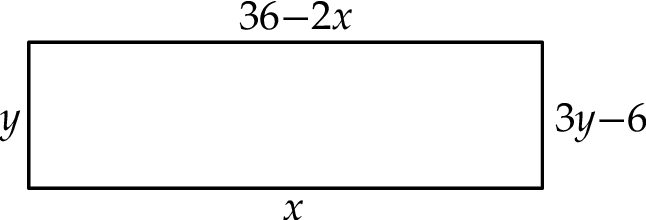
Które równanie nie opisuje poprawnej zależności między wartościami  i
i 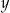 ?
?
A) 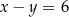 B)
B) 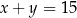 C)
C) 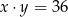 D)
D) 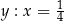
W układzie współrzędnych zaznaczono trójkąt 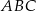 oraz punkt
oraz punkt 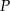 należący do boku
należący do boku 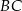 . Wszystkie współrzędne punktów
. Wszystkie współrzędne punktów 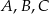 i
i 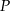 są liczbami całkowitymi.
są liczbami całkowitymi.
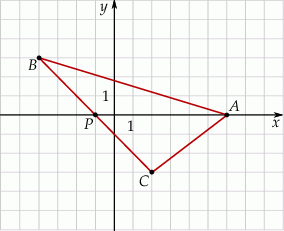
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 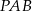 jest równe polu trójkąta jest równe polu trójkąta 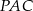 . . | P | F |
Pole trójkąta 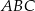 jest równe 21. jest równe 21. | P | F |
Jedną z jednostek używanych do mierzenia kątów są grady. Tworząc te jednostki dzielimy kąt pełny na 400 gradów. Miara w stopniach kąta o mierze 220 gradów jest równa
A) 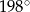 B)
B) 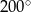 C)
C) 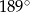 D)
D) 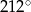
Jedną z jednostek używanych do mierzenia kątów są grady. Tworząc te jednostki dzielimy kąt pełny na 400 gradów. Kąt prosty wyrażony w gradach to
A) 150 gradów B) 200 gradów C) 100 gradów D) 50 gradów
Firma składa się z dwóch oddziałów. W marcu zysk pierwszego oddziału był równy 30 tys. zł, a drugiego oddziału 24 tys. zł. W kwietniu zysk pierwszego oddziału zmniejszył się o 10% w stosunku do marca, ale zysk całej firmy był taki sam jak w marcu.
O ile procent w stosunku do poprzedniego miesiąca zwiększył się w kwietniu zysk drugiego oddziału?
A) 10% B) 12,5% C) 8% D) 14,5%
Trzy koleżanki kupiły bilety autobusowe w tym samym automacie. Kamila kupiła 3 bilety 20–minutowe, 2 bilety 75–minutowe, jeden bilet 24–godzinny i zapłaciła za te bilety 28 zł. Justyna kupiła 2 bilety 20–minutowe, 3 bilety 75–minutowe, 4 bilety 24–godzinne i zapłaciła za te bilety 62 zł. Kasia kupiła jeden bilet 20–minutowy, jeden bilet 75–minutowy i jeden bilet 24–godzinny. Ile Kasia zapłaciła za bilety?
A) 20 zł B) 16 zł C) 18 zł D) 15 zł
Zależność między temperaturą wyrażoną w stopniach Celsjusza a temperaturą wyrażoną w stopniach Fahrenheita wyraża się wzorem 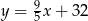 , gdzie
, gdzie  - temperatura w skali Celsjusza,
- temperatura w skali Celsjusza, 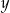 - temperatura w skali Fahrenheita. Zatem 122 stopnie Fahrenheita są równe
- temperatura w skali Fahrenheita. Zatem 122 stopnie Fahrenheita są równe
A) 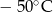 B)
B) 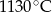 C)
C) 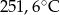 D)
D) 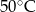
Zależność między temperaturą wyrażoną w stopniach Celsjusza a temperaturą wyrażoną w stopniach Fahrenheita wyraża się wzorem 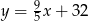 , gdzie
, gdzie  - temperatura w skali Celsjusza,
- temperatura w skali Celsjusza, 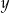 - temperatura w skali Fahrenheita. Zatem 59 stopnie Fahrenheita są równe
- temperatura w skali Fahrenheita. Zatem 59 stopnie Fahrenheita są równe
A) 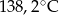 B)
B) 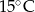 C)
C) 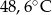 D)
D) 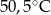
Zależność między temperaturą wyrażoną w stopniach Celsjusza a temperaturą wyrażoną w stopniach Fahrenheita wyraża się wzorem 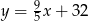 , gdzie
, gdzie  - temperatura w skali Celsjusza,
- temperatura w skali Celsjusza, 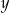 - temperatura w skali Fahrenheita. Zatem 113 stopnie Fahrenheita są równe
- temperatura w skali Fahrenheita. Zatem 113 stopnie Fahrenheita są równe
A) 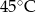 B)
B) 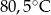 C)
C) 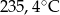 D)
D) 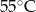
Wartość wyrażenia 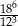 jest równa A/B.
jest równa A/B.
A) 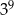 B)
B) 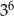
Wartość wyrażenia 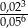 jest równa C/D.
jest równa C/D.
C) 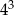 D)
D) 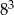
Wśród pewnej grupy osób przeprowadzono ankietę. Jedno z pytań brzmiało: Jaki jest twój ulubiony dzień tygodnia?. Każdy ankietowany wskazał tylko jeden dzień tygodnia. Rozkład udzielonych odpowiedzi na to pytanie przedstawiono na diagramie.
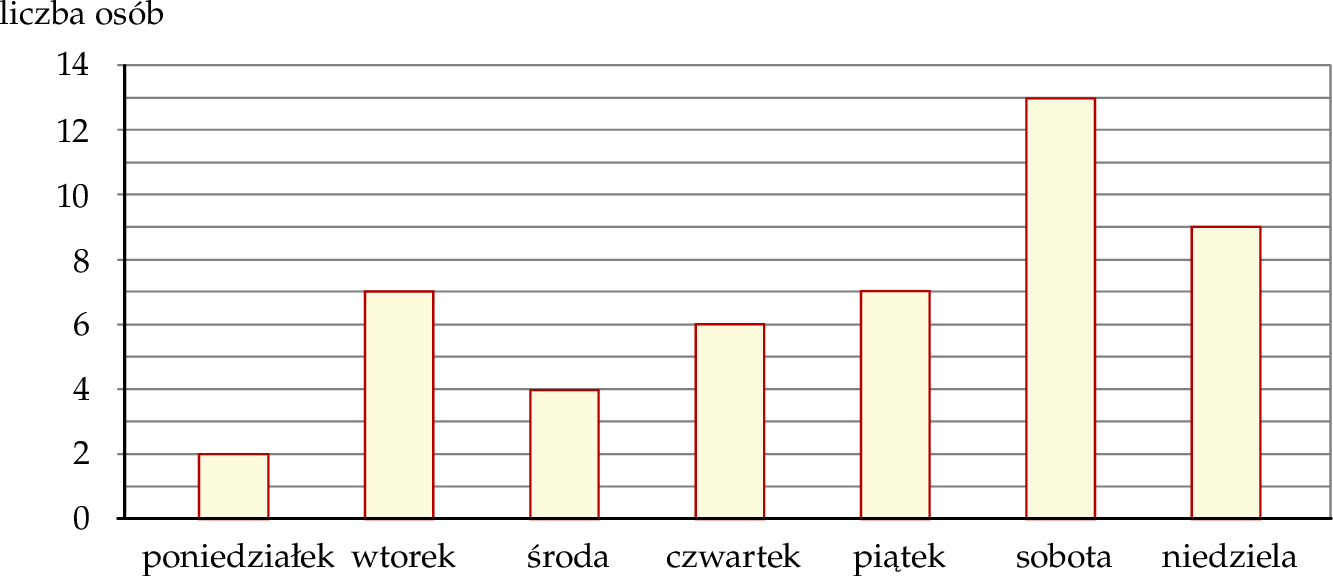
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Niedziela jest ulubionym dniem tygodnia dla mniej niż  liczby osób ankietowanych. liczby osób ankietowanych. | P | F |
| Ponad 50% ankietowanych osób jako ulubiony dzień tygodnia wskazało wtorek, czwartek lub sobotę. | P | F |
Maturzysta na rozwiązanie testu składającego się z 36 zadań przeznaczył 3 godziny. Średnia liczba sekund przeznaczonych na jedno zadanie jest równa
A) 300 B) 240 C) 30 D) 5
Szklane naczynie w kształcie stożka o promieniu podstawy 6 cm i wysokości 9 cm napełniono wodą do połowy wysokości (zobacz rysunek) i szczelnie zamknięto.
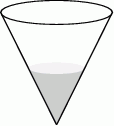
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość wlanej wody stanowi 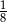 objętości naczynia. objętości naczynia. | P | F |
| Jeżeli naczynie odwrócimy i postawimy na podstawie stożka, to naczynie będzie wypełnione wodą do połowy wysokości. | P | F |
Pan Kazimierz po 10% podwyżce zarabia 2695 zł miesięcznie. Przed podwyżką pan Kazimierz zarabiał
A) 2500 zł. B) 2350 zł. C) 2400 zł. D) 2450 zł.
Dane są trzy liczby:
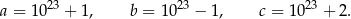
Które z tych liczb są podzielne przez 3?
A) Tylko liczby  i
i 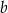 . B) Tylko liczba
. B) Tylko liczba 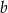 . C) Tylko liczby
. C) Tylko liczby 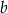 i
i  . D) Tylko liczba
. D) Tylko liczba  .
.
W tabeli przedstawiono procentowy podział uczestników obozu ze względu na wiek.
| Wiek uczestnika | Liczba uczestników |
| 10 lat | 20% |
| 12 lat | 40% |
| 14 lat | 25% |
| 16 lat | 15% |
Mediana wieku uczestników obozu jest równa
A) 12 lat B) 11 lat C) 10 lat D) 13 lat
Liczbę 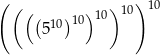 można przedstawić w postaci
można przedstawić w postaci
A) 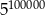 B)
B) 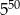 C)
C) 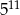 D)
D) 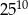
Liczbę 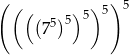 można przedstawić w postaci
można przedstawić w postaci
A) 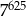 B)
B) 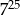 C)
C) 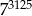 D)
D) 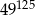
Średnia prędkość poruszania się mrówki to 50 centymetrów na minutę. Średnia prędkość biegnącego słonia to 39 kilometrów na godzinę. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Średnia prędkość biegnącego słonia jest 1300 razy większa od średniej prędkości mrówki. | P | F |
| W ciągu jednej godziny mrówka pokonuje dystans 30 metrów. | P | F |

