Janek w pierwszym semestrze otrzymał następujące oceny z matematyki: z prac klasowych 2, 3, 3, 4, z kartkówek 5, 5, 4, 4, 5, 5, z odpowiedzi ustnych 2, 3, 4. Oceny z prac klasowych mają wagę 0,5, z kartkówek 0,3, z odpowiedzi ustnych 0,2. Średnia ważona (zaokrąglona do dwóch miejsc po przecinku) ocen z matematyki Janka w pierwszym semestrze jest równa
A) 3,68 B) 3,58 C) 3,25 D) 1,23
/Szkoła podstawowa/Zadania testowe
Kasia w pierwszym semestrze otrzymała następujące oceny z matematyki: z prac klasowych 3, 4, 4, 2, z kartkówek 5, 4, 4, 3, 5, z zadań domowych 3, 4, 5. Oceny z prac klasowych mają wagę 5, z kartkówek 3, z zadania domowego 2. Średnia ważona (zaokrąglona do dwóch miejsc po przecinku) ocen z matematyki Kasi w pierwszym semestrze jest równa
A) 3,71 B) 4,6 C) 13,7 D) 11,41
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Graniastosłup może mieć 2019 ścian. | P | F |
| Ostrosłup może mieć 2019 krawędzi. | P | F |
Zaznacz zdanie fałszywe.
A) Każdy równoległobok posiada środek symetrii.
B) Każdy równoległobok posiada oś symetrii.
C) Każdy romb posiada środek symetrii.
D) Każdy romb posiada oś symetrii.
Bezrobocie w pewnym kraju wynosi 10%. Które z poniższych zdań jest fałszywe?
A) Jeżeli bezrobocie wzrośnie o 5 punktów procentowych, to będzie wynosiło 15%.
B) Jeżeli bezrobocie zmaleje o 3 punkty procentowe, to będzie wynosiło 7%.
C) Jeżeli bezrobocie spadnie o 5%, to będzie wynosiło 5%.
D) Jeżeli bezrobocie wzrośnie o 10%, to będzie wynosiło 11%.
Organizatorzy loterii fantowej przygotowali zestaw losów, w którym były dwa rodzaje losów: niebieskie i zielone. Losów niebieskich było dwa razy mniej niż losów zielonych i upoważniały one do odbioru cenniejszej nagrody. Uczestnicy loterii losowali po jednym losie, który po wylosowaniu był usuwany z zestawu. Pierwszy uczestnik loterii wyciągnął los niebieski, a drugi uczestnik wyciągnął los zielony.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo wyciągnięcia przez trzecią osobę losu niebieskiego jest równe 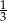 . . | P | F |
Prawdopodobieństwo wyciągnięcia przez pierwszą osobę losu zielonego było równe  . . | P | F |
Cenę  (w złotych) pewnego towaru obniżono najpierw o 30%, a następnie obniżono o 20% w odniesieniu do ceny obowiązującej w danym momencie. Po obydwu tych obniżkach cena towaru jest równa
(w złotych) pewnego towaru obniżono najpierw o 30%, a następnie obniżono o 20% w odniesieniu do ceny obowiązującej w danym momencie. Po obydwu tych obniżkach cena towaru jest równa
A) 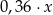 złotych. B)
złotych. B) 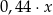 złotych.
złotych.
C) 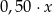 złotych. D)
złotych. D) 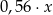 złotych.
złotych.
Bok kwadratu ma długość 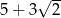 . Przekątna kwadratu ma długość A/B.
. Przekątna kwadratu ma długość A/B.
A) 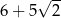 B) 11
B) 11
Pole kwadratu jest równe C/D.
C) 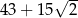 D)
D) 
Wyznaczając  z równania
z równania 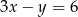 otrzymujemy:
otrzymujemy:
A) 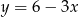 B)
B) 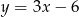 C)
C) 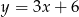 D)
D) 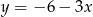
Grupa uczniów jechała pociągiem w góry. Jedna siódma uczniów miała miejsca przy oknie, jedna piąta uczniów miała miejsca przy korytarzu, a pozostali uczniowie mieli miejsca środkowe.
Jaki procent wszystkich uczniów stanowią uczniowie, którzy nie mieli miejsc przy korytarzu?
A) 75% B) 60% C) 20% D) 80%
Pole prostokąta, którego boki mają długości 0,002 mm i 500 km jest równe
A) 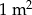 B)
B) 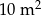 C)
C) 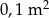 D)
D) 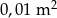
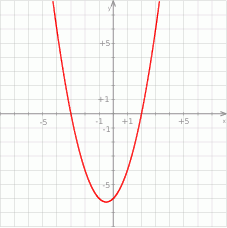
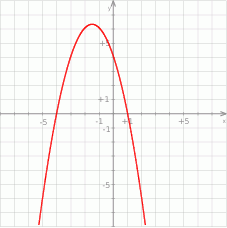
Przedstawiona na wykresie funkcja przyjmuje wartości ujemne jeżeli
A) 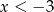 B)
B) 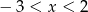 C)
C) 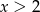 D)
D) 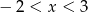
Przedstawiona na wykresie funkcja przyjmuje wartości dodatnie jeżeli
A) 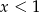 B)
B) 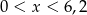 C)
C) 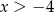 D)
D) 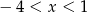
Poniżej podano kilka kolejnych potęg liczby 7.
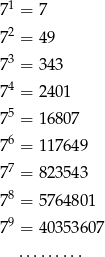
Cyfrą jedności liczby 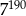 jest
jest
A) 1 B) 3 C) 7 D) 9
Poniżej podano kilka kolejnych potęg liczby 8.
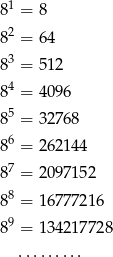
Cyfrą jedności liczby 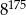 jest
jest
A) 4 B) 2 C) 8 D) 6
Słoń waży 5 ton, a waga mrówki jest równa 0,5 grama. Ile razy słoń jest cięższy od mrówki?
A) 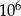 B)
B) 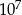 C) 10 D)
C) 10 D) 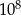
Wieża Eiffla ma wysokość 300 m, a pantofelek ma długość 0,3 mm. Ile razy wieża Eiffla jest wyższa od długości pantofelka?
A) 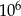 B)
B) 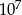 C) 1000 D)
C) 1000 D) 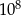
W pewnym zoo mieszkają słoń afrykański o masie 6 ton oraz góralek skalny o masie 3 kg. Masa słonia afrykańskiego jest większa niż masa góralka skalnego
A) 20 razy. B) 200 razy. C) 2 000 razy. D) 20 000 razy.
W klasie IIIa liczba dziewcząt stanowi  liczby wszystkich uczniów tej klasy. W klasie IIIa
liczby wszystkich uczniów tej klasy. W klasie IIIa
A) jest więcej chłopców niż dziewcząt.
B) liczba dziewcząt stanowi 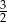 liczby chłopców.
liczby chłopców.
C) jest dwa razy więcej dziewcząt niż chłopców.
D) stosunek liczby chłopców do liczby dziewcząt jest równy 1:3.
W klasie IIIa liczba dziewcząt stanowi  liczby wszystkich uczniów tej klasy. W klasie IIIa
liczby wszystkich uczniów tej klasy. W klasie IIIa
A) jest cztery razy więcej dziewcząt niż chłopców.
B) stosunek liczby chłopców do liczby dziewcząt jest równy 1:3.
C) jest więcej chłopców niż dziewcząt.
D) liczba dziewcząt stanowi 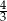 liczby chłopców.
liczby chłopców.
Do dzbanka wlano 2 jednakowe butelki soku.
Ile takich samych butelek wody należy dolać do dzbanka, aby sok stanowił 25% napoju?
A) 2 B) 4 C) 6 D) 8
Do pustej szklanki wlano 3 miarki syropu.
Ile takich samych miarek wody należy dolać do szklanki, aby syrop stanowił 30% napoju?
A) 10 B) 5 C) 6 D) 7
Dane są liczby 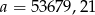 i
i 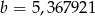 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba  jest 100 razy większa od liczby jest 100 razy większa od liczby 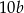 . . | P | F |
Liczba 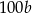 jest 1000 razy mniejsza od liczby jest 1000 razy mniejsza od liczby  . . | P | F |
Cenę telewizora obniżono o 15%, a następnie o 2%. Klient kupił telewizor po obniżonej cenie i dzięki temu zapłacił o 501 zł mniej, niż zapłaciłby przed obniżkami. Przed obniżkami ten telewizor kosztował
A) 2947 zł B) 4000 zł C) 3000 zł D) 2840 zł
Cenę laptopa podwyższono o 12%, a następnie o 19%. W wyniku tych podwyżek cena laptopa wzrosła o 832 zł. Przed podwyżkami ten laptop kosztował
A) 3332 zł B) 2500 zł C) 3000 zł D) 2375 zł
W trakcie kontroli jakości basenu rekreacyjnego napełniono go całkowicie wodą. Po pewnym czasie w basenie wykryto usterkę i częściowo go opróżniono. Następnie usterkę usunięto i basen ponownie napełniono wodą. Na zakończenie kontroli basen całkowicie opróżniono z wody.
Na wykresie przedstawiono jak zmieniała się w czasie kontroli objętość wody w basenie.
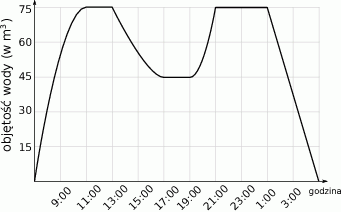
Ile wody spuszczono z basenu po wykryciu usterki?
A)
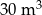 B)
B) 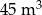 C)
C) 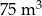 D)
D) 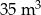
W trakcie kontroli jakości basenu rekreacyjnego napełniono go całkowicie wodą. Po pewnym czasie w basenie wykryto usterkę i częściowo go opróżniono. Następnie usterkę usunięto i basen ponownie napełniono wodą. Na zakończenie kontroli basen całkowicie opróżniono z wody.
Na wykresie przedstawiono jak zmieniała się w czasie kontroli objętość wody w basenie.
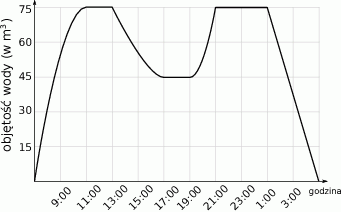
Na podstawie podanych informacji wybierz zdanie prawdziwe.
A) W trakcie kontroli więcej czasu poświęcono na napełnianie basenu, niż na jego opróżnianie.
B) Kontrola basenu trwała 11 godzin.
C) Częściowe opróżnienie basenu po wykryciu usterki trwało dłużej niż jego ponowne napełnienie po jej naprawieniu.
D) Basen był całkowicie wypełniony wodą przez 3 godziny.
W trakcie kontroli jakości basenu rekreacyjnego napełniono go całkowicie wodą. Po pewnym czasie w basenie wykryto usterkę i częściowo go opróżniono. Następnie usterkę usunięto i basen ponownie napełniono wodą. Na zakończenie kontroli basen całkowicie opróżniono z wody.
Na wykresie przedstawiono jak zmieniała się w czasie kontroli objętość wody w basenie.
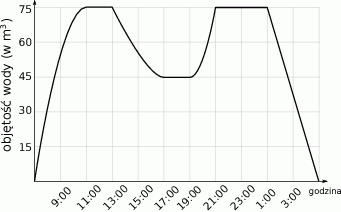
Podczas końcowego opróżniania basenu,
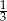 objętości wody usunięto w ciągu
objętości wody usunięto w ciąguA) 80 minut B) 40 minut C) 60 minut D) 70 minut
Do pojemnika wsypano 200 koralików białych i 300 czerwonych. Wymieszano je i zapakowano do woreczków po 50 sztuk. Okazało się, że w jednym z woreczków znalazły się tylko białe koraliki.
Wobec tego nie jest możliwe, aby
A) wszystkie pozostałe białe koraliki znajdowały się w trzech woreczkach.
B) w jednym z pozostałych woreczków nie było białych koralików.
C) w większości pozostałych woreczków znalazło się po 17 białych koralików.
D) w każdym z pozostałych woreczków było więcej koralików białych niż czerwonych.
Na boku 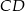 prostokąta
prostokąta 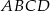 o bokach długości 12 cm i 20 cm wybrano punkt
o bokach długości 12 cm i 20 cm wybrano punkt 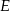 w ten sposób, że pole czworokąta
w ten sposób, że pole czworokąta 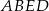 jest równe
jest równe 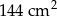 .
.
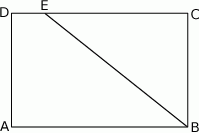
Długość odcinka 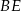 jest równa
jest równa
A) 20 B) 24 C) 18 D) 16

