Na którym rysunku zamalowano 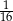 figury?
figury?

 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na którym rysunku zamalowano 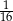 figury?
figury?

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 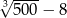 jest dodatnia. jest dodatnia. | P | F |
Liczba 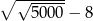 jest ujemna. jest ujemna. | P | F |
Podróż pociągiem z Olsztyna do Gdyni planowo trwa 2 godziny i 54 minuty. Pewnego dnia pociąg wyjechał z Olsztyna punktualnie o wyznaczonej godzinie, ale przyjechał do Gdyni z czterominutowym opóźnieniem o godzinie 17:31. Pociąg wyjechał z Olsztyna o godzinie
A) 14:27 B) 14:41 C) 14:31 D) 14:33
Ze zbioru liczb naturalnych dwucyfrowych nie większych niż 35 losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że wylosowana liczba będzie podzielna przez 5?
A) 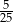 B)
B) 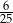 C)
C) 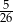 D)
D) 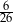
Ze zbioru kolejnych liczb naturalnych 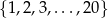 losujemy jedną liczbę. Prawdopodobieństwo, że wylosujemy liczbę podzielną przez 3 jest równe
losujemy jedną liczbę. Prawdopodobieństwo, że wylosujemy liczbę podzielną przez 3 jest równe
A) 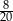 B)
B) 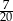 C)
C) 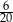 D)
D) 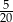
Ze zbioru liczb 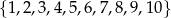 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby parzystej jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby parzystej jest równe
A) 0,5 B) 0,6 C) 0,4 D) 0,8
Ze zbioru liczb naturalnych dwucyfrowych losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 5, jest równe
A)  B)
B) 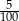 C)
C) 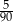 D)
D) 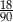
Ze zbioru liczb 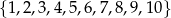 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby podzielnej przez 3 lub 4 jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby podzielnej przez 3 lub 4 jest równe
A) 0,5 B) 0,6 C) 0,4 D) 0,8
Dane są liczby 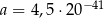 oraz
oraz 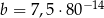 . Wtedy iloraz
. Wtedy iloraz 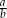 jest równy
jest równy
A) 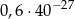 B)
B) 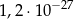 C)
C) 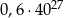 D)
D) 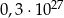
Poniższa tabela przedstawia temperaturę odczytywaną o tej samej porze w kolejnych dniach tygodnia.
| Poniedziałek | Wtorek | Środa | Czwartek | Piątek | Sobota | Niedziela |
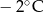 | 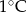 | 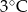 | 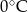 | 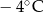 | 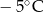 | 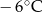 |
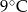 B)
B) 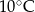 C)
C) 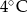 D)
D) 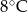
Poniższa tabela przedstawia temperaturę odczytywaną o tej samej porze w kolejnych dniach tygodnia.
| Poniedziałek | Wtorek | Środa | Czwartek | Piątek | Sobota | Niedziela |
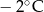 | 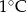 | 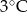 | 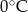 | 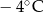 | 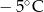 | 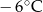 |
Średnia temperatura tego tygodnia była niższa niż 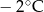 . . | P | F |
| Przez cztery kolejne dni tego tygodnia temperatura malała. | P | F |
Na rysunku przedstawiono czworokąt zbudowany z dwóch trójkątów prostokątnych. Dane są długości boków 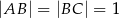 oraz
oraz 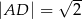 .
.
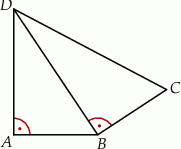
Długość boku 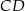 jest równa
jest równa
A) 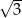 B) 2 C) 3 D)
B) 2 C) 3 D) 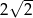
Na rysunku przedstawiono czworokąt zbudowany z dwóch trójkątów prostokątnych. Dane są długości boków 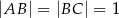 oraz
oraz 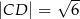 .
.
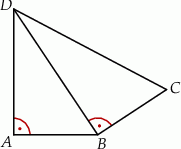
Długość boku 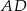 jest równa
jest równa
A) 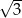 B) 2 C) 3 D)
B) 2 C) 3 D) 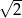
Firma „Poziomka” produkuje napój owocowy mieszając przecier owocowy i wodę w stosunku 2 : 7. Z 400 litrów przecieru owocowego można wyprodukować A/B napoju owocowego.
A) 1400 B) 1800
Do wyprodukowania 450 litrów napoju owocowego potrzeba C/D litrów wody.
C) 280 D) 350
Z odległości 33 m czubek drzewa widać po kątem 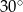 . Jak wysokie jest to drzewo?
. Jak wysokie jest to drzewo?
A) Około 16 m. B) Około 25 m. C) Około 19 m. D) Około 66 m.
Reszta z dzielenia liczby 55 przez 8 jest równa
A) 4 B) 5 C) 6 D) 7
Reszta z dzielenia liczby 65 przez 7 jest równa
A) 1 B) 2 C) 3 D) 5
Funkcja przedstawiona na wykresie przyjmuje wartości dodatnie dla
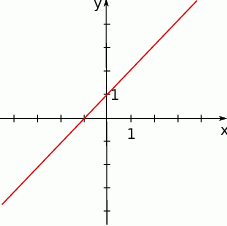
A) 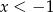 B)
B) 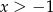 C)
C) 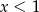 D)
D) 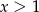
Funkcja przedstawiona na wykresie przyjmuje wartości dodatnie dla
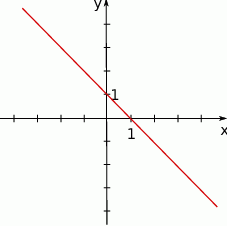
A) 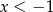 B)
B) 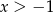 C)
C) 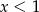 D)
D) 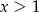
Funkcja przedstawiona na wykresie przyjmuje wartości ujemne dla
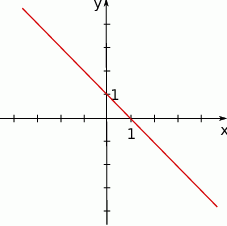
A) 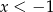 B)
B) 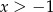 C)
C) 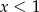 D)
D) 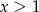
Janek w pierwszym semestrze otrzymał następujące oceny z matematyki: z prac klasowych 2, 3, 3, 4, z kartkówek 5, 5, 4, 4, 5, 5, z odpowiedzi ustnych 2, 3, 4. Oceny z prac klasowych mają wagę 0,5, z kartkówek 0,3, z odpowiedzi ustnych 0,2. Średnia ważona (zaokrąglona do dwóch miejsc po przecinku) ocen z matematyki Janka w pierwszym semestrze jest równa
A) 3,68 B) 3,58 C) 3,25 D) 1,23
Kasia w pierwszym semestrze otrzymała następujące oceny z matematyki: z prac klasowych 3, 4, 4, 2, z kartkówek 5, 4, 4, 3, 5, z zadań domowych 3, 4, 5. Oceny z prac klasowych mają wagę 5, z kartkówek 3, z zadania domowego 2. Średnia ważona (zaokrąglona do dwóch miejsc po przecinku) ocen z matematyki Kasi w pierwszym semestrze jest równa
A) 3,71 B) 4,6 C) 13,7 D) 11,41
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Graniastosłup może mieć 2019 ścian. | P | F |
| Ostrosłup może mieć 2019 krawędzi. | P | F |
Zaznacz zdanie fałszywe.
A) Każdy równoległobok posiada środek symetrii.
B) Każdy równoległobok posiada oś symetrii.
C) Każdy romb posiada środek symetrii.
D) Każdy romb posiada oś symetrii.
Bezrobocie w pewnym kraju wynosi 10%. Które z poniższych zdań jest fałszywe?
A) Jeżeli bezrobocie wzrośnie o 5 punktów procentowych, to będzie wynosiło 15%.
B) Jeżeli bezrobocie zmaleje o 3 punkty procentowe, to będzie wynosiło 7%.
C) Jeżeli bezrobocie spadnie o 5%, to będzie wynosiło 5%.
D) Jeżeli bezrobocie wzrośnie o 10%, to będzie wynosiło 11%.
Organizatorzy loterii fantowej przygotowali zestaw losów, w którym były dwa rodzaje losów: niebieskie i zielone. Losów niebieskich było dwa razy mniej niż losów zielonych i upoważniały one do odbioru cenniejszej nagrody. Uczestnicy loterii losowali po jednym losie, który po wylosowaniu był usuwany z zestawu. Pierwszy uczestnik loterii wyciągnął los niebieski, a drugi uczestnik wyciągnął los zielony.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo wyciągnięcia przez trzecią osobę losu niebieskiego jest równe 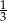 . . | P | F |
Prawdopodobieństwo wyciągnięcia przez pierwszą osobę losu zielonego było równe  . . | P | F |
Cenę  (w złotych) pewnego towaru obniżono najpierw o 30%, a następnie obniżono o 20% w odniesieniu do ceny obowiązującej w danym momencie. Po obydwu tych obniżkach cena towaru jest równa
(w złotych) pewnego towaru obniżono najpierw o 30%, a następnie obniżono o 20% w odniesieniu do ceny obowiązującej w danym momencie. Po obydwu tych obniżkach cena towaru jest równa
A) 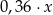 złotych. B)
złotych. B) 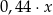 złotych.
złotych.
C) 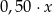 złotych. D)
złotych. D) 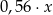 złotych.
złotych.
Bok kwadratu ma długość 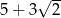 . Przekątna kwadratu ma długość A/B.
. Przekątna kwadratu ma długość A/B.
A) 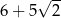 B) 11
B) 11
Pole kwadratu jest równe C/D.
C) 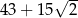 D)
D) 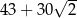
Wyznaczając 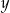 z równania
z równania 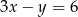 otrzymujemy:
otrzymujemy:
A) 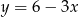 B)
B) 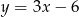 C)
C) 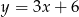 D)
D) 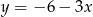
Grupa uczniów jechała pociągiem w góry. Jedna siódma uczniów miała miejsca przy oknie, jedna piąta uczniów miała miejsca przy korytarzu, a pozostali uczniowie mieli miejsca środkowe.
Jaki procent wszystkich uczniów stanowią uczniowie, którzy nie mieli miejsc przy korytarzu?
A) 75% B) 60% C) 20% D) 80%
