Na bokach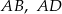 
i 
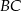rombu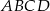 
wybrano odpowiednio punkty 
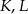i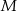 
w ten sposób, że odcink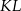i 
i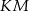 
są równoległe do przekątnych rombu. Wykaż, że odcinek 
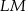przechodzi przez punkt przecięcia przekątnych rombu.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Romb/Udowodnij...
Kąt ostry rombu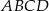 
ma miarę 
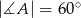. Na bokach 
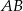i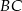 
wybrano punkty 
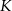i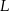 
w ten sposób, że 
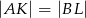. Uzasadnij, że trójkąt 
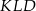jest trójkątem równobocznym.
Na bokach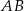 
i 
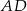rombu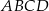 
wybrano odpowiednio punkty 
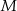i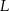 
w ten sposób, że 
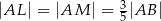. Odcinek 
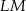jest styczny do okręgu wpisanego w romb 
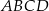. Punkt 
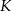jest punktem styczności okręgu wpisanego w ten romb z bokiem 
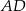(zobacz rysunek).
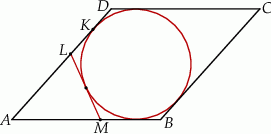
Wykaż, że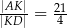 
.
Na bokach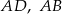 
i 
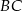rombu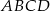 
wybrano punkty 
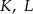i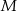 
w ten sposób, że 
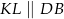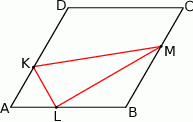
i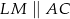 
. Uzasadnij, że pole czworokąta 
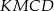stanowi połowę pola rombu.
Przekątne rombu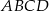 
przecinają się w punkcie 
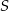. Punkty 
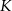i 
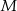leżą na przekątnej 
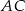tak, że 
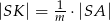i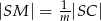 
. Punkty 
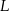i 
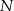leżą na przekątnej 
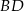tak, że 
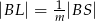i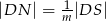 
(zobacz rysunek). Wykaż, że jeżeli stosunek pola czworokąta 
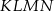do pola rombu 
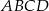jest równy 1:4, to 
.
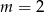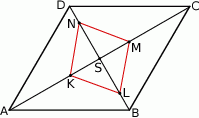
Wykaż, że środki boków rombu są wierzchołkami prostokąta.
Przekątne rombu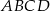 
przecinają się w punkcie 
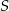. Punkt 
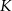jest takim punktem boku 
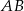, że odcinek 
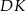jest wysokością rombu (zobacz rysunek).
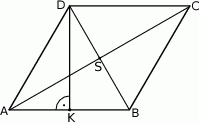
Wykaż, że jeżeli trójkąty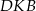 
i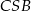 
są przystające, to punkt 
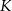jest środkiem odcinka 
.
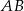Kąt ostry rombu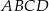 
ma miarę 
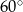. Na bokach 
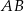i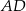 
tego rombu wybrano punkty – odpowiednio – 
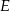i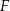 
takie, że 
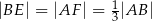. Odcink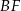i 
i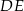 
przecinają się w punkcie 
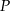(zobacz rysunek).
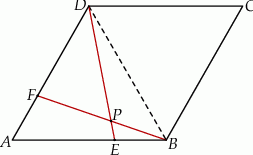
Wykaż, że punkt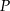 
leży na okręgu opisanym na trójkącie 
.
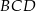W romb o boku 
wpisano dwa okręgi w ten sposób, że okręgi te są styczne zewnętrznie i każdy z nich jest styczny do dwóch sąsiednich boków rombu przecinających się pod kątem ostrym 
(zobacz rysunek).
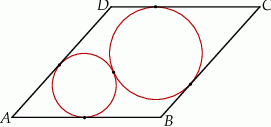
Udowodnij, że suma promieni tych okręgów jest równa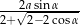 
.
