Janek, Tomek i Łukasz zbierali pieniądze na zakup piłki. Janek dał 60% potrzebnej kwoty, Tomek dał 40% pozostałej części. Łukasz dołożył brakujące 48 zł. Ile kosztowała piłka?
/Szkoła średnia/Zadania z treścią/Procenty
Firma 
zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy 
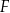, którzy otrzymują płacę miesięczną w danej wysokości.
Liczba pracowników firmy 
, których miesięczna płaca brutto nie przewyższa 5 000 zł, stanowi (w zaokrągleniu do 1%)
A) 91% liczby wszystkich pracowników tej firmy.
B) 78% liczby wszystkich pracowników tej firmy.
C) 53% liczby wszystkich pracowników tej firmy.
D) 22% liczby wszystkich pracowników tej firmy.
Pan Alojzy postanowił co miesiąc odkładać pewną sumę pieniędzy. W pierwszym miesiącu odłożył 100 zł, a w każdym następnym odkładał o 5% więcej niż w poprzednim. Razem z panem Alojzym oszczędzanie rozpoczęła jego małżonka, przy czym odłożyła ona w pierwszym miesiącu 110 zł, a w każdym następnym odkładała o 3% więcej, niż w poprzednim. Oblicz, która z tych dwóch osób zaoszczędzi więcej pieniędzy po roku oszczędzania.
Firma zatrudniła w tym samym czasie małżeństwo na następujących warunkach: mąż otrzymał za pierwszy przepracowany miesiąc 1200 zł, a żona 1600 zł. Pensja męża będzie wzrastać co miesiąc o 100 zł, a żony o 40 zł.
- Po przepracowaniu którego miesiąca, żona odbierze pensję w wysokości 2680 zł?
- Ile miesięcy muszą przepracować małżonkowie, aby suma zarobków męża stanowiła 150% sumy zarobków żony (licząc od początku zatrudnienia)?
Jeden z pracowników pewnej firmy otrzymuje stałą pensję miesięczną za 168 przepracowanych godzin oraz dodatkowe wynagrodzenie za nadgodziny. Stawka za godzinę nadliczbową jest o 50% większa niż stawka za godzinę etatową. W styczniu pracownik ten miał 8 nadgodzin i otrzymał razem 2700 zł.
- Oblicz stawkę za godzinę nadliczbową oraz stawkę za godzinę etatową.
- Napisz wzór funkcji wyrażającej wynagrodzenie pracownika w zależności od liczby przepracowanych godzin nadliczbowych.
Zmieszano 1 kg solanki o zawartości 18% soli i 2 kg solanki o zawartości 15% soli. Ile procent soli zawiera ta mieszanina?
Ukryj
Podobne zadania
Szklankę octu o stężeniu 10% zmieszano z trzema szklankami octu sześcioprocentowego. Jakie jest stężenie otrzymanej mieszanki?
Zmieszano 2 kg solanki o zawartości 12% soli i 1 kg solanki o zawartości 18% soli. Ile procent soli zawiera ta mieszanina?
Jeden z boków prostokąta zwiększono o 10%, a drugi zmniejszono o 10%. Czy pole tego prostokąta uległo zmianie? Jeżeli tak, to o ile procent?
Ukryj
Podobne zadania
Dany jest prostokąt o bokach 
i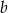 
. Długość boku 
zmniejszono o 20% a długość boku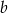 
zwiększono o 10%. Oblicz, ile procent pola prostokąta o bokach 
i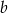 
stanowi pole prostokąta otrzymanego po dokonaniu zmian długości boków.
Pan Piotrek postanowił założyć lokatę, wpłacając 10000 zł na okres jednego roku. Bank proponuje oprocentowanie kapitału 12% w stosunku rocznym, z kapitalizacją odsetek co kwartał. Oblicz, jaką kwotę będzie dysponować pan Piotrek po roku, wiedząc, że podatek od uzyskanego w ten sposób dochodu wynosi 19% i jest pobierany przy każdej kapitalizacji.
Pan Adam wpłacił na rachunek w funduszu inwestycyjnym pewną kwotę pieniędzy. Po roku stan rachunku zwiększył się o 4,5%, w drugim roku zmniejszył się o 5%, a w trzecim roku wzrósł o 4%. Wiedząc, że stan rachunku pana Adama po trzech latach oszczędzania wynosi 1548,69 zł oblicz jaką kwotę pan Adam początkowo wpłacił na ten rachunek.
Dwaj rowerzyści pokonują trasę między punktam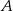i 
i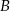 
. O ile procent średnia prędkość drugiego rowerzysty musi być większa od średniej prędkości pierwszego rowerzysty, aby przyjechał on o 20% szybciej?
Wyprowadź wzór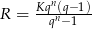 
na wysokość raty 
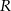kredytu udzielonego w kwocie 
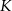, przy założeniu, że:
– spłata tego kredytu jest rozłożona na 
równych rat płaconych miesięcznie;
– pierwszą ratę wpłacamy po miesiącu od daty udzielenia kredytu;
– roczne oprocentowanie kredytu jest równe 
i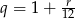 
.
Cenę sukienki obniżano dwukrotnie, za każdym razem o ten sam procent. W wyniku tych obniżek cena sukienki ze 100 zł spadła do 96,04 zł. Oblicz, o ile procent za każdym razem obniżano cenę sukienki.
Pan Kwiatkowski i pan Kowalski wpłacili swoje oszczędności o łącznej wartości 10 000 zł do różnych banków. Pan Kwiatkowski ulokował swoje oszczędności w banku, w którym oprocentowanie rocznie wynosiło 12% zaś pan Kowalski - w banku, który proponował oprocentowanie roczne w wysokości 14%. Po roku łączna kwota odsetek wynosiła 1384 zł. Ile złotych ulokował w banku każdy z panów?
Złotnik ma dwie sztabki wykonane z różnych stopów. Pierwsza sztabka składa się ze 120 g złota i 30 g miedzi, a druga sztabka składa się ze 180 g złota i 20 g miedzi. Ile gramów każdej sztabki powinien wziąć złotnik, aby po stopieniu tych dwóch kawałków otrzymać sztabkę składającą się ze 172 g złota i 28 g miedzi?
