Czworokąt w podstawie/Dowolny - zadania z matematyki

/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Dowolny/Czworokąt w podstawie

Podstawą graniastosłupa jest trapez równoramienny o podstawach długości 56 cm i 40 cm oraz wysokości 15 cm. Wiedząc, że wysokość graniastosłupa jest równa 10 cm, oblicz jego pole powierzchni całkowitej.

Ukryj Podobne zadania

Podstawą graniastosłupa jest trapez równoramienny o podstawach długości 56 cm i 40 cm oraz wysokości 15 cm. Wiedząc, że wysokość graniastosłupa jest równa 20 cm, oblicz jego pole powierzchni całkowitej.

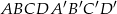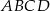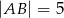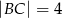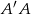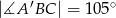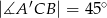Podstawą graniastosłupa prostego ′ ′ ′ ′ ABCDA B C D jest równoległobok ABCD o bokach długości |AB | = 5 i |BC | = 4 . Oblicz długość wysokości A ′A graniastosłupa jeżeli |∡A ′BC | = 1 05∘ oraz |∡A ′CB | = 45∘ .

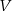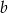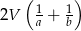Podstawą graniastosłupa prostego o objętości jest równoległobok o bokach długości i . Wykaż, że pole powierzchni bocznej tego graniastosłupa jest nie mniejsze niż ( ) 2V 1 + 1 a b .

Podstawą graniastosłupa prostego 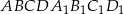ABCDA 1B1C1D 1 jest trapez równoramienny 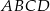ABCD wpisany w okrąg o środku 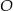i promieniu 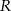. Dłuższa podstawa 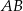trapezu jest średnicą tego okręgu, a krótsza ma długość (zobacz rysunek). Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem o mierze . Wyznacz objętość tego graniastosłupa jako funkcję promienia 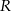, długości podstawy i miary kąta .

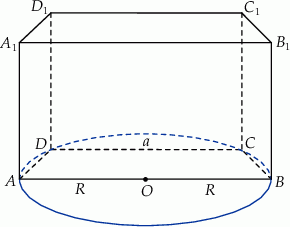
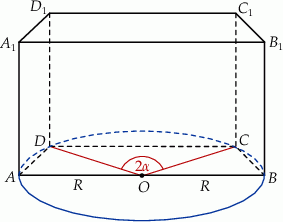
Podstawą graniastosłupa prostego 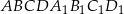ABCDA 1B 1C1D 1 jest trapez równoramienny 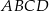ABCD wpisany w okrąg o środku 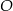i promieniu 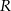. Dłuższa podstawa 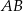trapezu jest średnicą tego okręgu, a krótsza – cięciwą odpowiadającą kątowi środkowemu o mierze 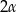(zobacz rysunek). Przekątna ściany bocznej zawierającej ramię trapezu jest nachylona do płaszczyzny podstawy pod kątem o mierze . Wyznacz objętość tego graniastosłupa jako funkcję promienia 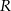i miary kąta .

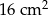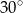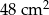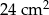Dany jest graniastosłup, którego podstawą jest równoległobok o polu 2 16 cm i kącie ostrym 30∘ . Oblicz objętość graniastosłupa jeżeli pola jego ścian są równe 48 cm 2 i 24 cm 2 .