Dany jest ostrosłup prawidłowy trójkątny, w którym długość krawędzi podstawy jest równa  . Kąt między krawędzią boczną i krawędzią podstawy ma miarę
. Kąt między krawędzią boczną i krawędzią podstawy ma miarę 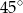 . Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
. Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy trójkątny/Przekroje
Dany jest ostrosłup prawidłowy trójkątny, w którym długość krawędzi podstawy jest równa  . Kąt między krawędzią boczną i krawędzią podstawy ma miarę
. Kąt między krawędzią boczną i krawędzią podstawy ma miarę 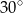 . Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
. Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
Dany jest ostrosłup prawidłowy trójkątny 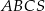 o podstawie
o podstawie 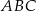 . Krawędź podstawy tego ostrosłupa ma długość
. Krawędź podstawy tego ostrosłupa ma długość  . Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem
. Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 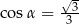 . Przez środek
. Przez środek 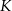 krawędzi
krawędzi 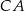 i środek
i środek 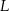 krawędzi
krawędzi 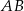 poprowadzono płaszczyznę
poprowadzono płaszczyznę 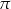 prostopadłą do płaszczyzny
prostopadłą do płaszczyzny 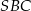 . Oblicz pole otrzymanego przekroju.
. Oblicz pole otrzymanego przekroju.
Krawędź boczna ostrosłupa prawidłowego trójkątnego jest nachylona do płaszczyzny podstawy pod kątem  . Przez krawędź podstawy tego ostrosłupa poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy pod katem
. Przez krawędź podstawy tego ostrosłupa poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy pod katem 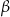 , i która przecina przeciwległą krawędź ostrosłupa (zobacz rysunek).
, i która przecina przeciwległą krawędź ostrosłupa (zobacz rysunek).
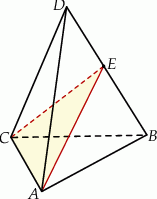
Oblicz stosunek pola powierzchni otrzymanego przekroju do pola powierzchni podstawy ostrosłupa jeżeli wiadomo, że 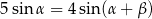 .
.
Ostrosłup prawidłowy trójkątny przecięto płaszczyzną, która przechodzi przez krawędź podstawy długości  oraz jest prostopadła do przeciwległej krawędzi bocznej. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem
oraz jest prostopadła do przeciwległej krawędzi bocznej. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem  . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
Wysokość ostrosłupa prawidłowego trójkątnego jest równa 4, a krawędź podstawy ma długość 1. Ostrosłup przecięto płaszczyzną, która przechodzi przez krawędź podstawy oraz jest prostopadła do przeciwległej krawędzi bocznej. Oblicz pole powierzchni tego przekroju.
Dany jest ostrosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość  i krawędź boczna jest od niej dwa razy dłuższa. Oblicz cosinus kąta między krawędzią boczną i krawędzią podstawy ostrosłupa. Narysuj przekrój ostrosłupa płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej krawędzi bocznej i oblicz pole tego przekroju.
i krawędź boczna jest od niej dwa razy dłuższa. Oblicz cosinus kąta między krawędzią boczną i krawędzią podstawy ostrosłupa. Narysuj przekrój ostrosłupa płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej krawędzi bocznej i oblicz pole tego przekroju.
Ostrosłup prawidłowy trójkątny przecięto płaszczyzną przechodzącą przez krawędź podstawy długości  i środek wysokości ostrosłupa. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem
i środek wysokości ostrosłupa. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem  . Oblicz objętość i pole powierzchni bocznej ostrosłupa.
. Oblicz objętość i pole powierzchni bocznej ostrosłupa.

