Okrąg i koło/Planimetria - zadania z matematyki

/Szkoła średnia/Geometria/Planimetria/Okrąg i koło

Ramiona kąta ostrego o mierze 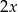przecięto prostą 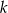prostopadłą do dwusiecznej kąta, która jest odległa o 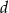od jego wierzchołka. W ten kąt wpisano dwa okręgi, każdy styczny do obu ramion kąta i prostej 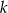. Oblicz odległość środków tych okręgów.

Przez punkty 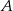i 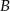okręgu poprowadzono styczne, które przecięły się w punkcie .

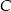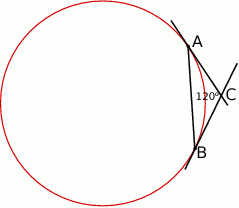
Wykaż, że jeżeli 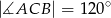|∡ACB | = 12 0∘ , to cięciwa 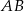ma długość równą długości promienia okręgu.

Do dwóch okręgów o promieniach długości 3 cm i 10 cm poprowadzono wspólną styczną tak, że okręgi znajdują się po różnych stronach tej stycznej. Odległość między środkami okręgów wynosi 39 cm. Oblicz długość odcinka między punktami styczności.

Dane są trzy okręgi o środkach 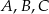A ,B ,C i promieniach równych odpowiednio 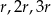r,2r,3r . Każde dwa z tych okręgów są zewnętrznie styczne: pierwszy z drugim w punkcie 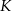, drugi z trzecim w punkcie 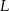i trzeci z pierwszym w punkcie 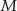. Oblicz stosunek pola trójkąta 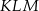KLM do pola trójkąta ABC .

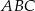W danym okręgu o środku 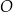poprowadzono cięciwy 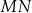i 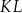, które przecięły się w punkcie .

ZINFO-FIGURE

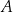Wykaż, że trójkąty 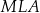i 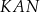są podobne.
Wiedząc, że 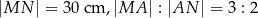oraz 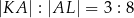, oblicz długość cięciwy .

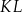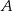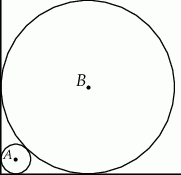
Dwa okręgi o środkach i 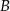są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek promienia większego z tych okręgów do promienia mniejszego jest równy 3 + 2√ 2- .

Ukryj Podobne zadania

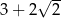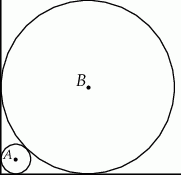
Dwa okręgi o środkach 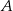i 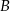są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek obwodu większego z tych okręgów do obwodu mniejszego jest równy 3 + 2√ 2- .

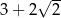Dane jest koło o promieniu długości 16 cm. W kole tym poprowadzono cięciwę opartą na łuku odpowiadającym kątowi środkowemu o mierze 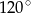120∘ . Znajdź odległość tej cięciwy od środka koła.

Do dwóch okręgów przecinających się w punktach 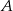i 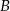poprowadzono wspólną styczną 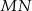, przy czym punkt 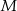należy do pierwszego, a punkt 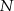do drugiego okręgu. Wykaż, że prosta 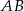dzieli odcinek 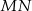na połowy.

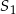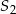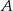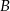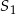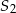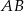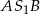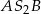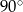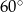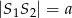Dwa okręgi o środkach S 1 i przecinają się w punktach i , przy czym punkty S 1 i S 2 leżą po przeciwnych stronach prostej . Miary kątów AS 1B i AS 2B wynoszą odpowiednio 90∘ i 60∘ . Wyznacz długości promieni tych okręgów wiedząc, że |S S | = a 1 2 .

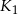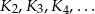Koło ma promień długości . Wewnątrz tego koła rysujemy kolejno koła K 2,K3,K 4,... takie, że kolejne koło ma średnicę równą promieniowi poprzedniego koła.

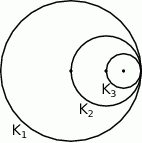
Wyznacz pole koła 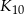K10 .

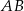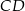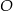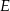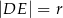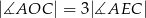Średnica i cięciwa okręgu o środku i promieniu przecinają się w punkcie takim, że |DE | = r . Wykaż, że |∡AOC | = 3|∡AEC | .

Ukryj Podobne zadania

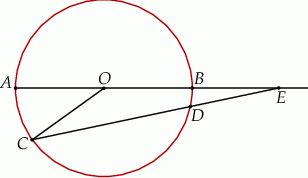
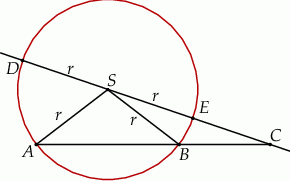
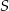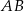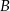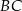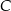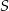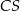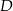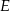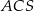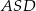Dany jest okrąg o środku w punkcie i promieniu . Na przedłużeniu cięciwy poza punkt odłożono odcinek równy promieniowi danego okręgu. Przez punkty i poprowadzono prostą. Prosta przecina dany okrąg w punktach i (zobacz rysunek). Wykaż, że jeżeli miara kąta ACS jest równa , to miara kąta ASD jest równa .

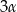Dany jest okrąg o promieniu 11 oraz punkt 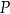oddalony o 7 od środka okręgu. Przez punkt 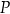poprowadzono cięciwę o długości 18. W jakim stosunku punkt 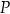podzielił tę cięciwę na dwa odcinki?

Strona 6 z 6