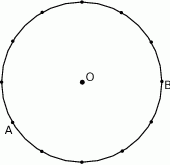
Punkty  i
i  leżą na okręgu o środku
leżą na okręgu o środku  i dzielą ten okrąg na dwa łuki, których stosunek długości jest równy 7:5. Oblicz miarę kąta środkowego opartego na krótszym łuku.
i dzielą ten okrąg na dwa łuki, których stosunek długości jest równy 7:5. Oblicz miarę kąta środkowego opartego na krótszym łuku.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkty 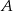 i
i 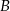 leżą na okręgu o środku
leżą na okręgu o środku 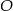 i dzielą ten okrąg na dwa łuki, których stosunek długości jest równy 7:5. Oblicz miarę kąta środkowego opartego na krótszym łuku.
i dzielą ten okrąg na dwa łuki, których stosunek długości jest równy 7:5. Oblicz miarę kąta środkowego opartego na krótszym łuku.

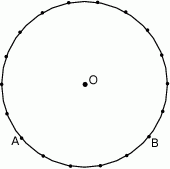
Punkty 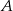 i
i 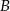 leżą na okręgu o środku
leżą na okręgu o środku 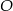 i dzielą ten okrąg na dwa łuki, których stosunek długości jest równy 13:5. Oblicz miarę kąta środkowego opartego na krótszym łuku.
i dzielą ten okrąg na dwa łuki, których stosunek długości jest równy 13:5. Oblicz miarę kąta środkowego opartego na krótszym łuku.
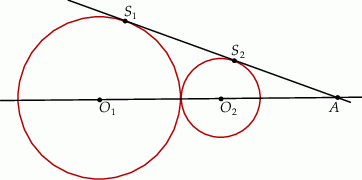
Dane są okręgi o środkach 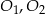 oraz promieniu 2. Jeden z nich jest styczny wewnętrznie, a drugi styczny zewnętrznie do okręgu o środku
oraz promieniu 2. Jeden z nich jest styczny wewnętrznie, a drugi styczny zewnętrznie do okręgu o środku 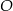 i promieniu 5. Wiadomo, że
i promieniu 5. Wiadomo, że 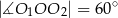 . Oblicz długość odcinka
. Oblicz długość odcinka 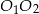 .
.
Cięciwa okręgu tworzy kąt 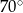 z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
Cięciwa okręgu tworzy kąt 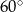 z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
Cięciwa okręgu tworzy kąt 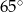 z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
z promieniem przechodzącym przez jej koniec. Oblicz obydwa kąty środkowe wyznaczone przez tę cięciwę.
W okręgu o promieniu długości  kreślimy średnicę
kreślimy średnicę 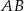 oraz taką cięciwę
oraz taką cięciwę 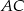 , że
, że 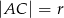 . Jaką częścią okręgu jest łuk
. Jaką częścią okręgu jest łuk 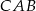 ?
?
W pierścieniu kołowym cięciwa zewnętrznego okręgu ma długość 10 i jest styczna do wewnętrznego okręgu (zobacz rysunek).
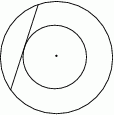
Wykaż, że pole tego pierścienia można wyrazić wzorem, w którym nie występują promienie wyznaczających go okręgów.
Dwie cięciwy przecinają się wewnątrz okręgu tak, że odcinki jednej z nich mają długości 8 i 6, a odcinki drugiej pozostają w stosunku 2:3. Podaj długości odcinków drugiej cięciwy.
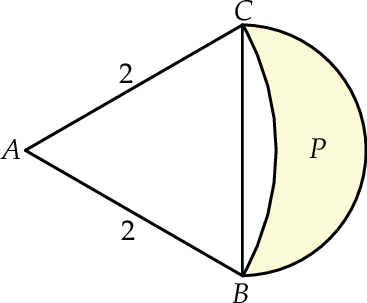
Trójkąt 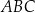 jest trójkątem równobocznym o boku długości 2. Obszar
jest trójkątem równobocznym o boku długości 2. Obszar 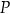 jest zawarty między półokręgiem o średnicy
jest zawarty między półokręgiem o średnicy 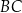 i łukiem okręgu o środku
i łukiem okręgu o środku 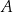 przechodzącym przez punkty
przechodzącym przez punkty 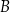 i
i  . Oblicz pole obszaru
. Oblicz pole obszaru  .
.
Z punktu  leżącego na okręgu poprowadzono średnicę
leżącego na okręgu poprowadzono średnicę 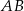 i cięciwę
i cięciwę 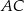 , które tworzą kąt o mierze
, które tworzą kąt o mierze 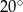 . Przez punkt
. Przez punkt 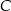 poprowadzono styczną do okręgu przecinającą prostą
poprowadzono styczną do okręgu przecinającą prostą 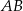 w punkcie
w punkcie 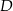 . Oblicz miary pozostałych kątów trójkąta
. Oblicz miary pozostałych kątów trójkąta 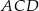 .
.
W okręgu o promieniu 8 cm poprowadzono cięciwę 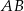 . Długość łuku
. Długość łuku 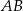 jest równa
jest równa 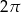 . Oblicz miarę kąta ostrego zawartego między cięciwą
. Oblicz miarę kąta ostrego zawartego między cięciwą 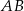 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 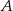 .
.
W okręgu o promieniu 5 cm poprowadzono cięciwę 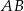 . Długość łuku
. Długość łuku 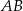 jest równa
jest równa 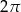 . Oblicz miarę kąta ostrego zawartego między cięciwą
. Oblicz miarę kąta ostrego zawartego między cięciwą 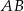 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 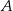 .
.
Dany jest okrąg 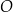 . Przez punkt
. Przez punkt 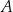 poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio –
poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio – 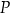 oraz
oraz 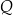 . Przez punkt
. Przez punkt 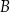 leżący na odcinku
leżący na odcinku 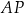 poprowadzono styczną do tego okręgu w punkcie
poprowadzono styczną do tego okręgu w punkcie 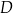 , która przecięła odcinek
, która przecięła odcinek  w punkcie
w punkcie 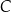 (zobacz rysunek).
(zobacz rysunek).
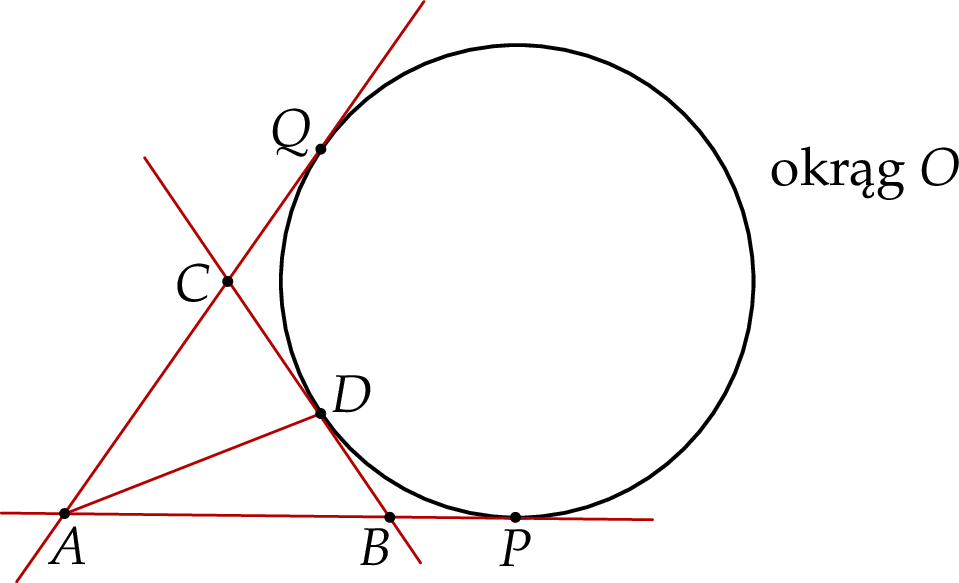
Wykaż, że jeżeli 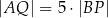 oraz
oraz 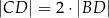 , to trójkąt
, to trójkąt 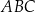 jest równoramienny.
jest równoramienny.
Dany jest okrąg 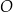 . Przez punkt
. Przez punkt 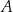 poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio –
poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio – 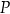 oraz
oraz 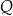 . Przez punkt
. Przez punkt 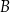 leżący na odcinku
leżący na odcinku 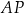 poprowadzono styczną do tego okręgu w punkcie
poprowadzono styczną do tego okręgu w punkcie 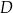 , która przecięła odcinek
, która przecięła odcinek 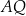 w punkcie
w punkcie 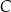 (zobacz rysunek).
(zobacz rysunek).
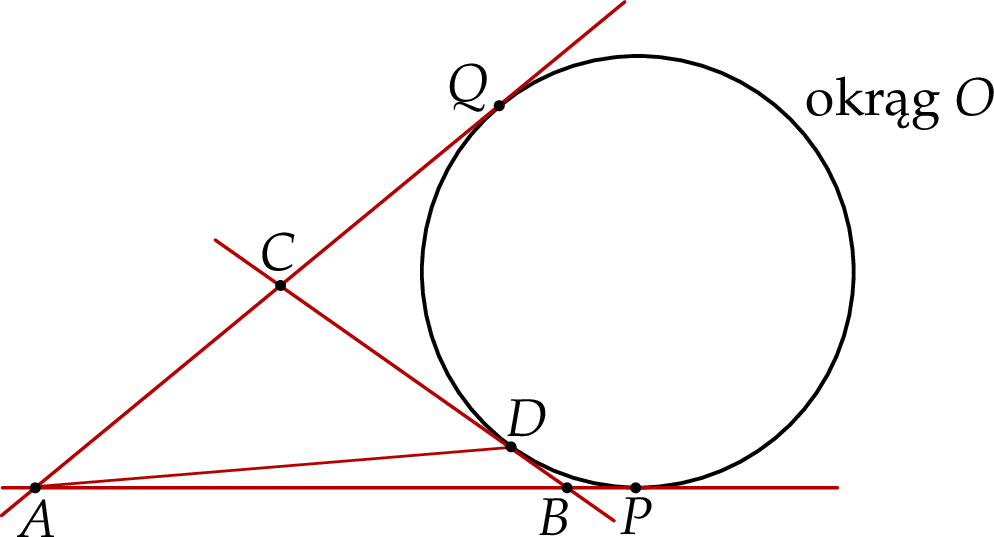
Wykaż, że jeżeli 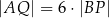 oraz
oraz 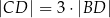 , to trójkąt
, to trójkąt 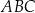 nie jest równoramienny.
nie jest równoramienny.
Przez punkt styczności dwóch okręgów poprowadzono sieczną. Udowodnij, że wypukłe kąty środkowe oparte na łukach wyznaczonych przez tę sieczną na okręgach mają równe miary.
Dwa okręgi są styczne zewnętrznie w punkcie 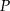 . Poprowadzono prostą, styczną do obu okręgów odpowiednio w punktach
. Poprowadzono prostą, styczną do obu okręgów odpowiednio w punktach 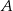 i
i 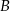 (
(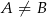 ). Wykaż, że kąt
). Wykaż, że kąt 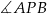 jest prosty.
jest prosty.
Dwa okręgi są zewnętrznie styczne w punkcie 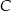 oraz są styczne do prostej
oraz są styczne do prostej  w punktach
w punktach  i
i  odpowiednio (zobacz rysunek).
odpowiednio (zobacz rysunek).
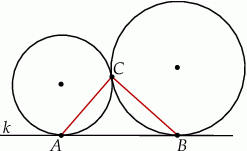
Uzasadnij, że trójkąt 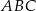 jest prostokątny.
jest prostokątny.
Okręgi 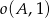 ,
, 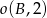 i
i 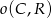 są parami styczne zewnętrznie. Oblicz
są parami styczne zewnętrznie. Oblicz 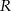 , jeśli
, jeśli 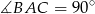 .
.
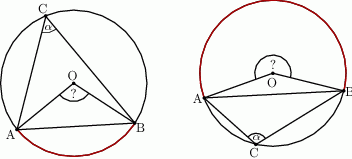
Oblicz miary kątów środkowych 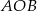 zaznaczonych na rysunkach, jeśli dana jest miara kąta wpisanego
zaznaczonych na rysunkach, jeśli dana jest miara kąta wpisanego 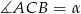 .
.
Średnica 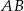 i cięciwa
i cięciwa 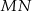 okręgu przecinają się w punkcie
okręgu przecinają się w punkcie 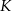 . Kąt
. Kąt 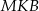 ma miarę
ma miarę 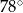 , a kąt środkowy oparty na łuku
, a kąt środkowy oparty na łuku 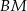 ma miarę
ma miarę 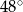 . Wyznacz miarę kąta
. Wyznacz miarę kąta 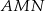 .
.
Dane są 2 koła styczne zewnętrznie o promieniach 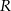 i
i  (
(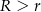 ) oraz środkach
) oraz środkach 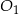 i
i 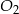 . Do tych kół poprowadzono wspólną styczną, która jest styczna do tych okręgów w punktach
. Do tych kół poprowadzono wspólną styczną, która jest styczna do tych okręgów w punktach 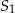 i
i 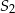 odpowiednio (
odpowiednio (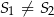 ). Oblicz pole trójkąta
). Oblicz pole trójkąta 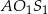 , gdzie
, gdzie 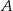 jest punktem przecięcia się prostych
jest punktem przecięcia się prostych 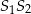 i
i 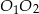 .
.
Prosta  jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie  . Oblicz miarę zaznaczonego kąta
. Oblicz miarę zaznaczonego kąta  jeśli
jeśli 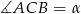 .
.
Punkty  ,
,  ,
, 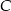 dzielą okrąg na trzy łuki, których stosunek długości wynosi
dzielą okrąg na trzy łuki, których stosunek długości wynosi 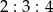 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 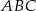 .
.
Punkty 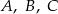 leżą na okręgu o środku
leżą na okręgu o środku  i dzielą ten okrąg na trzy łuki, których stosunek długości jest równy 3:4:5. Oblicz miary kątów trójkąta
i dzielą ten okrąg na trzy łuki, których stosunek długości jest równy 3:4:5. Oblicz miary kątów trójkąta  .
.
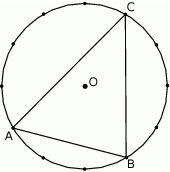
Punkty  dzielą okrąg na trzy łuki
dzielą okrąg na trzy łuki 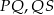 i
i 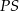 . Długości łuków
. Długości łuków 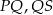 i
i 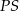 pozostają w stosunku 1:2:3. Oblicz miary kątów trójkąta
pozostają w stosunku 1:2:3. Oblicz miary kątów trójkąta 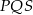 .
.
Punkty 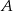 ,
, 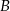 ,
, 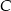 dzielą okrąg na trzy łuki, których stosunek długości wynosi
dzielą okrąg na trzy łuki, których stosunek długości wynosi 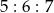 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 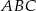 .
.
Odległość między środkami okręgów o promieniach 2 i 7 wynosi 13. Prosta 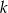 jest styczna do obu okręgów w punktach
jest styczna do obu okręgów w punktach 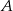 i
i 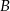 . Oblicz długość odcinka
. Oblicz długość odcinka 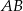 . Rozważ dwa przypadki.
. Rozważ dwa przypadki.
Trójkąt 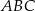 jest trójkątem równobocznym o boku długości
jest trójkątem równobocznym o boku długości  . Wykaż, że łuk okręgu opisanego na tym trójkącie zawarty między wierzchołkami
. Wykaż, że łuk okręgu opisanego na tym trójkącie zawarty między wierzchołkami 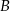 i
i 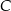 ma długość większą niż
ma długość większą niż 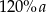 .
.
Trójkąt 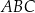 jest trójkątem równobocznym o boku długości
jest trójkątem równobocznym o boku długości  . Wykaż, że łuk okręgu wpisanego w ten trójkąt zawarty między dwoma kolejnymi punktami styczności tego okręgu z bokami trójkąta ma długość większą niż
. Wykaż, że łuk okręgu wpisanego w ten trójkąt zawarty między dwoma kolejnymi punktami styczności tego okręgu z bokami trójkąta ma długość większą niż 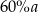 .
.

Z punktu 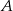 leżącego na okręgu poprowadź cięciwę
leżącego na okręgu poprowadź cięciwę 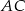 o długości równej promieniowi okręgu oraz średnicę
o długości równej promieniowi okręgu oraz średnicę 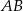 . Wyznacz miary kątów wewnętrznych trójkąta
. Wyznacz miary kątów wewnętrznych trójkąta 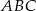 .
.
