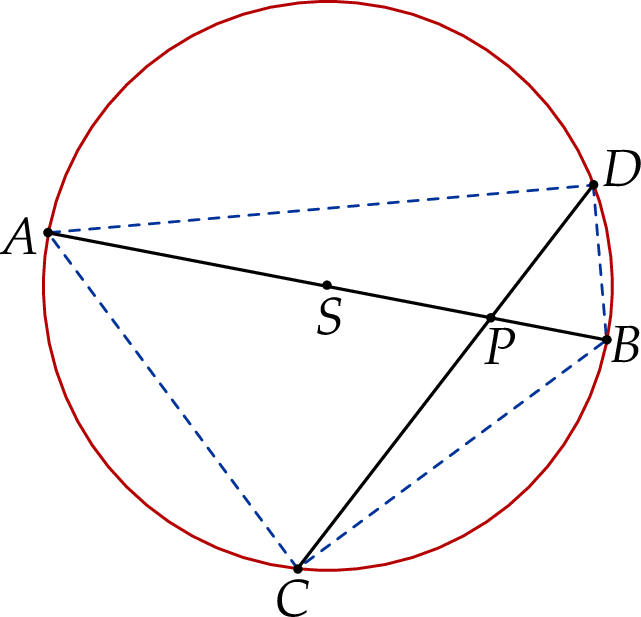
Trzy różne punkty  i
i  leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie  . Odcinek
. Odcinek 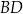 jest średnicą tego okręgu. Styczne
jest średnicą tego okręgu. Styczne 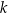 i
i 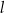 do tego okręgu, odpowiednio w punktach
do tego okręgu, odpowiednio w punktach 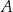 i
i 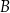 , przecinają się w punkcie
, przecinają się w punkcie 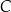 (zobacz rysunek poniżej).
(zobacz rysunek poniżej).

Wykaż, że trójkąty 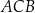 i
i 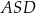 są podobne.
są podobne.

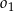 ,
, 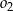 i
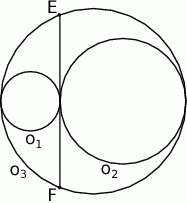
i 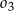 . Okręgi
. Okręgi 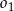 ,
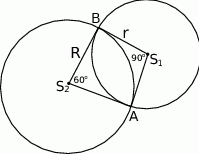
, 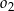 są styczne zewnętrznie, jednocześnie są styczne wewnętrznie do okręgu
są styczne zewnętrznie, jednocześnie są styczne wewnętrznie do okręgu 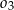 (patrz rysunek). Promienie okręgów
(patrz rysunek). Promienie okręgów 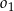 i
i 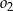 są odpowiednio równe
są odpowiednio równe 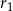 i
i 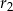 , a środki wszystkich trzech okręgów leżą na jednej prostej. Uzasadnij, że długość odcinka
, a środki wszystkich trzech okręgów leżą na jednej prostej. Uzasadnij, że długość odcinka 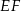 jest równa
jest równa 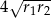 , gdzie odcinek
, gdzie odcinek 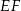 jest cięciwą okręgu
jest cięciwą okręgu 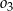 i zawiera się we wspólnej stycznej okręgów
i zawiera się we wspólnej stycznej okręgów 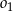 i
i 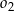 .
. 
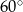 . Wyznacz stosunek długości promieni tych okręgów.
. Wyznacz stosunek długości promieni tych okręgów. 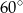 . Wyznacz stosunek długości promieni tych okręgów.
. Wyznacz stosunek długości promieni tych okręgów.  . Okręgi o średnicach
. Okręgi o średnicach 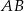 i
i 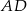 przecinają się w punktach
przecinają się w punktach 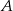 i
i 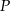 .
. 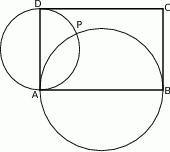
 i
i  leżą na jednej prostej.
leżą na jednej prostej.  . Okręgi o średnicach
. Okręgi o średnicach 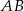 i
i 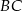 przecinają się w punktach
przecinają się w punktach 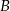 i
i 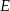 .
. 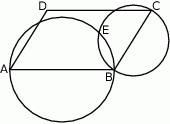
 i
i  leżą na jednej prostej.
leżą na jednej prostej.  i
i 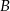 są punktami wspólnymi dwóch okręgów, a odcinki
są punktami wspólnymi dwóch okręgów, a odcinki 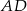 i
i 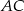 ich średnicami.
ich średnicami. 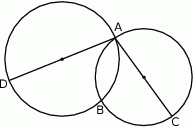
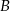 leży na prostej przechodzącej przez punkty
leży na prostej przechodzącej przez punkty 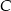 i
i 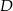 .
. 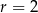 i
i 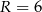 są styczne zewnętrznie i są styczne do wspólnej prostej
są styczne zewnętrznie i są styczne do wspólnej prostej 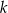 . Wykaż, że prosta
. Wykaż, że prosta 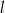 przechodząca przez środki
przechodząca przez środki 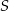 i
i 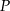 tych okręgów przecina prostą
tych okręgów przecina prostą 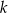 pod kątem
pod kątem 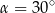 (zobacz rysunek).
(zobacz rysunek). 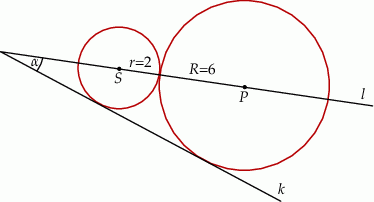
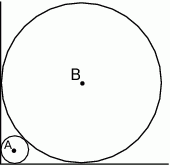
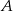 i
i 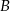 są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek pola większego z tych okręgów do pola mniejszego jest równy
są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek pola większego z tych okręgów do pola mniejszego jest równy 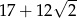 .
. 
 , jako ze środków zakreślono 4 okręgi o promieniu
, jako ze środków zakreślono 4 okręgi o promieniu 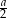 . Znajdź promienie okręgów stycznych do tych czterech okręgów jednocześnie.
. Znajdź promienie okręgów stycznych do tych czterech okręgów jednocześnie. 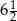 poprowadzono dwie prostopadłe cięciwy. Różnica ich długości jest równa 7. Oblicz długości tych cięciw.
poprowadzono dwie prostopadłe cięciwy. Różnica ich długości jest równa 7. Oblicz długości tych cięciw. 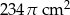 . Oblicz promienie tych kół, jeżeli wiadomo, że obwód większego koła jest o 400% większy od obwodu mniejszego koła.
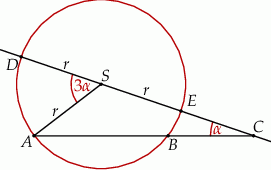
. Oblicz promienie tych kół, jeżeli wiadomo, że obwód większego koła jest o 400% większy od obwodu mniejszego koła. 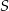 i promieniu
i promieniu  . Na przedłużeniu cięciwy
. Na przedłużeniu cięciwy 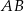 poza punkt
poza punkt 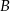 odłożono odcinek
odłożono odcinek 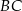 . Przez punkty
. Przez punkty 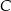 i
i 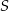 poprowadzono prostą. Prosta
poprowadzono prostą. Prosta 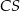 przecina dany okrąg w punktach
przecina dany okrąg w punktach 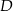 i
i 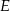 (zobacz rysunek). Wykaż, że jeżeli miara kąta
(zobacz rysunek). Wykaż, że jeżeli miara kąta 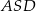 jest trzy razy większa od miary kąta
jest trzy razy większa od miary kąta 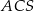 , to
, to 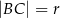 .
. 
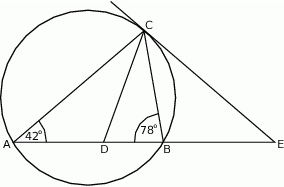
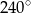 . Oblicz miarę kąta środkowego.
. Oblicz miarę kąta środkowego. 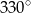 . Oblicz miarę kąta wpisanego.
. Oblicz miarę kąta wpisanego.  o środku w punkcie
o środku w punkcie 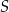 . Średnica
. Średnica 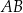 tego okręgu przecina cięciwę
tego okręgu przecina cięciwę 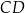 w punkcie
w punkcie 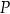 (zobacz rysunek). Ponadto:
(zobacz rysunek). Ponadto: 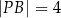 ,
, 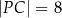 oraz
oraz 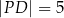 .
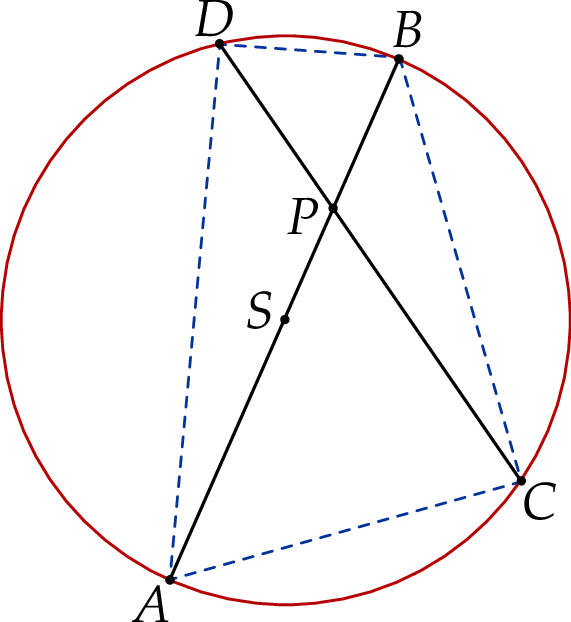
. 
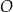 .
. 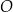 o środku w punkcie
o środku w punkcie 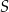 . Średnica
. Średnica 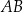 tego okręgu przecina cięciwę
tego okręgu przecina cięciwę 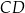 w punkcie
w punkcie 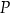 (zobacz rysunek). Ponadto:
(zobacz rysunek). Ponadto: 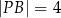 ,
, 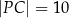 oraz
oraz 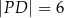 .
. 
 .
.  i
i  przecinają się w punktach
przecinają się w punktach 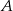 i
i 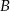 , przy czym punkty
, przy czym punkty 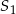 i
i 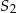 leżą po przeciwnych stronach prostej
leżą po przeciwnych stronach prostej 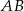 .
. 
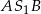 i
i 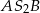 wynoszą odpowiednio
wynoszą odpowiednio 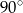 i
i 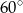 . Wyznacz stosunek
. Wyznacz stosunek 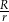 długości promieni tych okręgów.
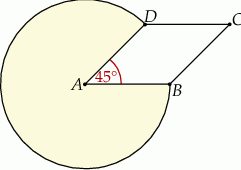
długości promieni tych okręgów. 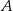 (zacieniowany obszar) jeśli pole rombu
(zacieniowany obszar) jeśli pole rombu 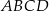 wynosi
wynosi 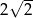 , a kąt ostry rombu ma miarę
, a kąt ostry rombu ma miarę 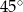 .
. 
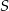 poprowadzono cięciwę, która nie jest średnicą. Punkt
poprowadzono cięciwę, która nie jest średnicą. Punkt 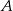 dzieli tę cięciwę na dwa odcinki o długościach 11 i 29. Odcinek
dzieli tę cięciwę na dwa odcinki o długościach 11 i 29. Odcinek 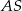 ma długość 15. Oblicz promień tego koła.
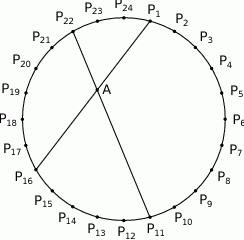
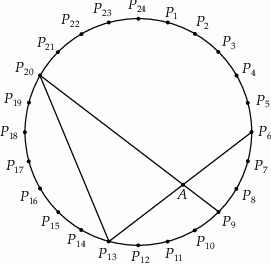
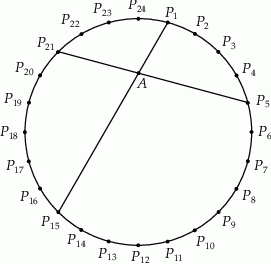
ma długość 15. Oblicz promień tego koła. 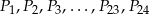 dzielą okrąg na 24 równe łuki (zobacz rysunek). Punkt
dzielą okrąg na 24 równe łuki (zobacz rysunek). Punkt 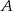 jest punktem przecięcia cięciw
jest punktem przecięcia cięciw 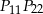 i
i 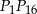 .
. 
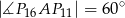 .
. 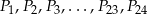 dzielą okrąg na 24 równe łuki (zobacz rysunek). Punkt
dzielą okrąg na 24 równe łuki (zobacz rysunek). Punkt 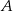 jest punktem przecięcia cięciw
jest punktem przecięcia cięciw 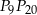 i
i 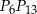 .
. 
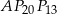 jest równoramienny.
jest równoramienny. 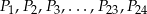 dzielą okrąg na 24 równe łuki (zobacz rysunek). Punkt
dzielą okrąg na 24 równe łuki (zobacz rysunek). Punkt 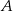 jest punktem przecięcia cięciw
jest punktem przecięcia cięciw  i
i  .
. 
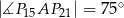 .
. 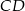 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 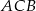 trójkąta
trójkąta 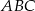 . Kąty trójkąta
. Kąty trójkąta 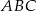 mają miary
mają miary 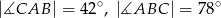 . Styczna do okręgu opisanego na tym trójkącie w punkcie
. Styczna do okręgu opisanego na tym trójkącie w punkcie 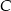 przecina prostą
przecina prostą 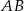 w punkcie
w punkcie 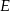 (zobacz rysunek). Oblicz, ile stopni ma każdy z kątów trójkąta
(zobacz rysunek). Oblicz, ile stopni ma każdy z kątów trójkąta 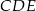 .
.