Dwa okręgi przecinają się w punktach 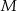 i
i 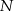 . Przez punkt
. Przez punkt 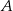 pierwszego okręgu prowadzimy proste
pierwszego okręgu prowadzimy proste 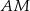 i
i 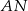 , przecinające drugi okrąg w punktach
, przecinające drugi okrąg w punktach 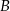 i
i 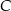 . Udowodnij, że styczna w punkcie
. Udowodnij, że styczna w punkcie 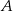 do pierwszego okręgu jest równoległa do prostej
do pierwszego okręgu jest równoległa do prostej 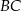 .
.
/Szkoła średnia/Geometria/Planimetria/Okrąg i koło
Dwa okręgi przecinają się w punktach 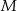 i
i 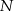 . Przez punkt
. Przez punkt 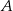 pierwszego okręgu prowadzimy proste
pierwszego okręgu prowadzimy proste 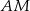 i
i 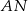 , przecinające drugi okrąg w punktach
, przecinające drugi okrąg w punktach 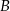 i
i 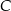 . Udowodnij, że styczna w punkcie
. Udowodnij, że styczna w punkcie 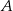 do pierwszego okręgu jest równoległa do prostej
do pierwszego okręgu jest równoległa do prostej 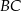 .
.
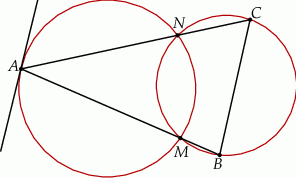
Środek 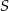 okręgu opisanego na trójkącie równoramiennym
okręgu opisanego na trójkącie równoramiennym 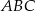 , o ramionach
, o ramionach 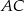 i
i 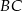 , leży wewnątrz tego trójkąta (zobacz rysunek).
, leży wewnątrz tego trójkąta (zobacz rysunek).
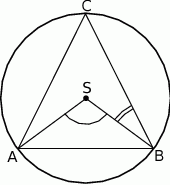
Wykaż, że miara kąta wypukłego 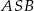 jest cztery razy większa od miary kąta wypukłego
jest cztery razy większa od miary kąta wypukłego 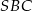 .
.
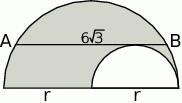
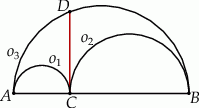
Z półkola o promieniu  wycięto półkole o średnicy
wycięto półkole o średnicy  (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 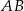 jest styczna do mniejszego półkola i jest równoległa do średnicy większego półkola. Oblicz pole zacieniowanego obszaru.
jest styczna do mniejszego półkola i jest równoległa do średnicy większego półkola. Oblicz pole zacieniowanego obszaru.
W okrąg o środku 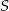 wpisany jest trójkąt równoramienny
wpisany jest trójkąt równoramienny 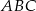 o kącie między ramionami
o kącie między ramionami 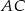 i
i 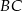 równym
równym 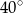 . Przez wierzchołek
. Przez wierzchołek 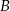 i środek okręgu
i środek okręgu 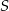 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 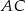 trójkąta w punkcie
trójkąta w punkcie 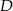 . Wyznacz miarę kąta
. Wyznacz miarę kąta 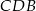 .
.
Dane są cztery okręgi. Każdy z nich jest styczny zewnętrznie do dokładnie dwóch spośród trzech pozostałych okręgów. Udowodnij, że punkty styczności tych okręgów są wierzchołkami czworokąta, na którym można opisać okrąg.
Różnica promieni dwóch okręgów współśrodkowych jest równa 3. W okręgu o większym promieniu poprowadzono cięciwę styczną do drugiego okręgu. Cięciwa ta ma długość 10. Oblicz długość promieni tych okręgów.
Przez środek 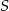 cięciwy
cięciwy 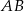 okręgu poprowadzono cięciwę
okręgu poprowadzono cięciwę 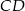 , przy czym
, przy czym 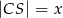 i
i 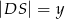 . Oblicz długość cięciwy
. Oblicz długość cięciwy 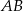 .
.
Prosta 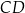 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 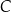 . Uzasadnij, że jeśli
. Uzasadnij, że jeśli 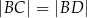 , to
, to 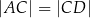 .
.
W półkole o średnicy 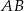 wpisano okrąg styczny do średnicy
wpisano okrąg styczny do średnicy 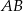 w jej środku. Znajdź promień okręgu stycznego jednocześnie do półokręgu
w jej środku. Znajdź promień okręgu stycznego jednocześnie do półokręgu 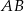 , do wpisanego okręgu oraz do średnicy
, do wpisanego okręgu oraz do średnicy 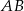 jeżeli
jeżeli 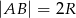 .
.
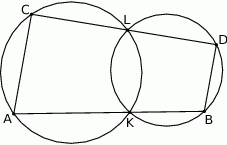
Dwa okręgi przecinają się w punktach 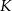 i
i 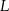 . Przez punkty
. Przez punkty 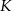 i
i 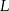 poprowadzono proste, które przecinają dane okręgi w punktach
poprowadzono proste, które przecinają dane okręgi w punktach 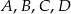 tak, jak pokazano to na poniższym rysunku. Wykaż, że
tak, jak pokazano to na poniższym rysunku. Wykaż, że 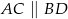 .
.
Cięciwa 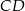 okręgu o środku
okręgu o środku 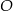 przecina średnicę
przecina średnicę 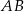 tego okręgu w punkcie
tego okręgu w punkcie 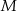 (rysunek). Kąt środkowy oparty na łuku
(rysunek). Kąt środkowy oparty na łuku 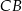 ma miarę
ma miarę 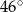 , a
, a 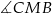 ma miarę
ma miarę 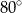 . Oblicz
. Oblicz 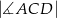 .
.
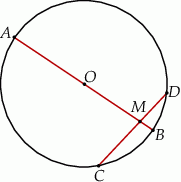
Cięciwa 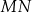 okręgu o środku
okręgu o środku 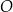 przecina średnicę
przecina średnicę 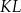 tego okręgu w punkcie
tego okręgu w punkcie 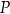 (rysunek). Kąt środkowy oparty na łuku
(rysunek). Kąt środkowy oparty na łuku 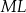 ma miarę
ma miarę 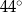 , a
, a 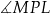 ma miarę
ma miarę 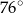 . Oblicz
. Oblicz 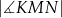 .
.
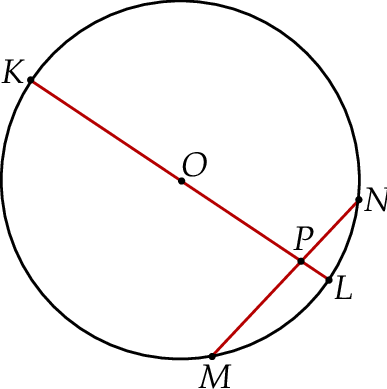
Na okręgu o środku 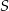 wybrano punkty
wybrano punkty 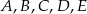 w ten sposób, że odcinek
w ten sposób, że odcinek 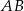 jest średnicą okręgu oraz
jest średnicą okręgu oraz 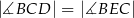 (zobacz rysunek).
(zobacz rysunek).
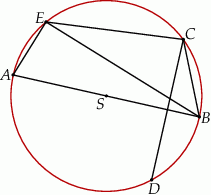
Wykaż, że proste 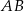 i
i 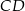 są prostopadłe.
są prostopadłe.
Dwa okręgi o promieniach  i
i 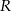 (
(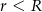 ) są styczne zewnętrznie. Prosta
) są styczne zewnętrznie. Prosta 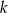 nie przechodzi przez punkt wspólny tych okręgów i jest styczna do każdego z nich. Znajdź promień okręgu stycznego zewnętrznie do danych okręgów i stycznego do prostej
nie przechodzi przez punkt wspólny tych okręgów i jest styczna do każdego z nich. Znajdź promień okręgu stycznego zewnętrznie do danych okręgów i stycznego do prostej 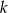 . Rozważ dwa przypadki.
. Rozważ dwa przypadki.
Dane są dwa kąty wpisane oparte na tym samym łuku. Wykaż, że dwusieczne tych kątów przetną się w punkcie należącym do okręgu.
Okręgi 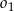 i
i 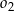 są styczne zewnętrznie oraz oba są styczne wewnętrznie do okręgu
są styczne zewnętrznie oraz oba są styczne wewnętrznie do okręgu 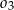 . Środki wszystkich trzech okręgów leżą na jednej prostej, a cięciwa
. Środki wszystkich trzech okręgów leżą na jednej prostej, a cięciwa 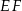 okręgu
okręgu 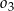 jest wspólną styczną okręgów
jest wspólną styczną okręgów 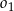 i
i 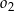 . Oblicz długość odcinka
. Oblicz długość odcinka 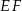 jeżeli promienie okręgów
jeżeli promienie okręgów 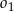 i
i 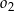 są odpowiednio równe
są odpowiednio równe 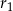 i
i 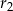 .
.
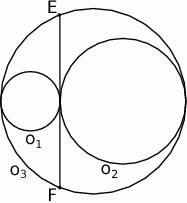
Na średnicy 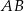 półokręgu
półokręgu 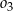 wybrano punkt
wybrano punkt 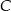 i na odcinkach
i na odcinkach 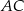 i
i 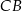 jako na średnicach skonstruowano półokręgi
jako na średnicach skonstruowano półokręgi 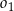 i
i 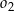 . Odcinek
. Odcinek 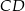 jest odcinkiem wspólnej stycznej półokręgów
jest odcinkiem wspólnej stycznej półokręgów 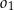 i
i 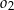 . Oblicz długość odcinka
. Oblicz długość odcinka 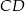 jeżeli promienie półokręgów
jeżeli promienie półokręgów 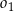 i
i 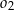 są odpowiednio równe
są odpowiednio równe 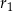 i
i 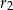 .
.
W okręgu narysowano dwie średnice 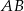 i
i 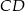 . Udowodnij, że czworokąt
. Udowodnij, że czworokąt 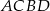 jest prostokątem.
jest prostokątem.
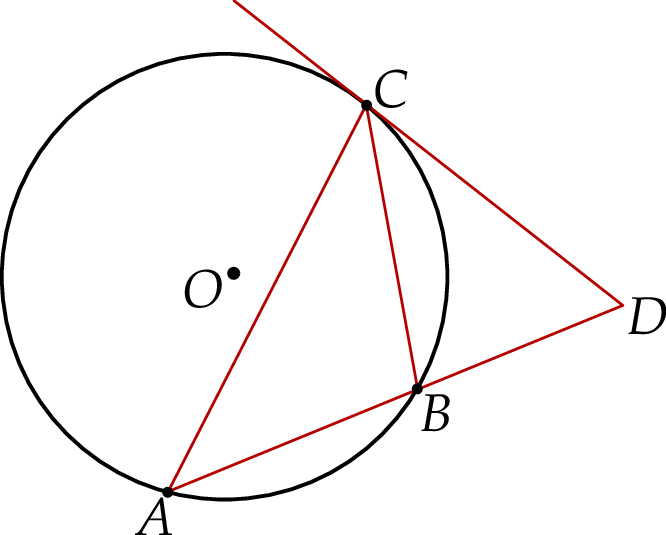
Dany jest okrąg 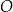 o środku w punkcie
o środku w punkcie 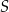 . Przedłużenie średnicy
. Przedłużenie średnicy 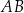 tego okręgu przecina przedłużenie cięciwy
tego okręgu przecina przedłużenie cięciwy 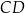 w punkcie
w punkcie 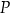 (zobacz rysunek). Ponadto:
(zobacz rysunek). Ponadto: 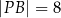 ,
, 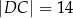 oraz
oraz 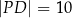 .
.
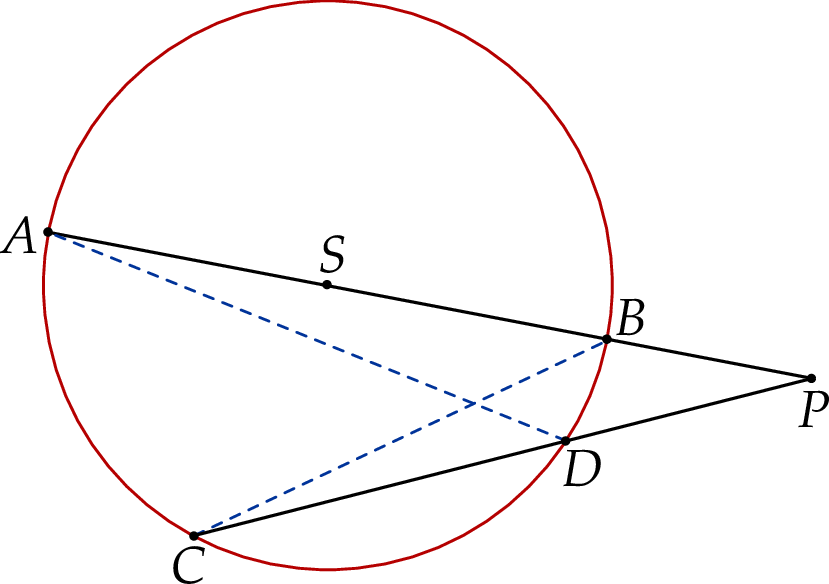
Oblicz promień okręgu 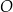 .
.
W półkolu z końca średnicy poprowadzono cięciwę, która tworzy ze średnicą kąt o mierze 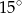 . Oblicz w jakim stosunku zostało podzielone pole tego półkola.
. Oblicz w jakim stosunku zostało podzielone pole tego półkola.
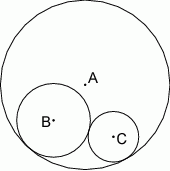
Na rysunku okręgi o środkach 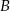 i
i 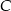 są styczne zewnętrznie i jednocześnie są styczne wewnętrznie do okręgu o środku w punkcie
są styczne zewnętrznie i jednocześnie są styczne wewnętrznie do okręgu o środku w punkcie 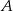 . Wykaż, że jeśli
. Wykaż, że jeśli 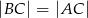 , to długość odcinka
, to długość odcinka 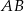 jest równa długości średnicy okręgu o środku w punkcie
jest równa długości średnicy okręgu o środku w punkcie  .
.
Wyznacz miarę łukową kąta środkowego w okręgu o promieniu 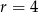 , opartego na łuku długości
, opartego na łuku długości 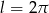 . Podaj miarę tego kąta w stopniach.
. Podaj miarę tego kąta w stopniach.
Wyznacz miarę łukową kąta środkowego w okręgu o promieniu 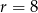 , opartego na łuku długości
, opartego na łuku długości 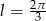 . Podaj miarę tego kąta w stopniach.
. Podaj miarę tego kąta w stopniach.
Wyznacz miarę łukową kąta środkowego w okręgu o promieniu 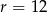 , opartego na łuku długości
, opartego na łuku długości 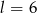 . Podaj miarę tego kąta w stopniach.
. Podaj miarę tego kąta w stopniach.
Wyznacz miarę łukową kąta środkowego w okręgu o promieniu 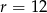 , opartego na łuku długości
, opartego na łuku długości 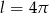 . Podaj miarę tego kąta w stopniach.
. Podaj miarę tego kąta w stopniach.

