Dane są dwa okręgi zewnętrznie styczne oraz styczne wewnętrznie do trzeciego. Środki okręgów tworzą trójkąt równoramienny o bokach długości 1 i 2. Znajdź długości promieni tych okręgów (rozważ dwa przypadki).
/Szkoła średnia/Geometria/Planimetria/Okrąg i koło
W okrąg o promieniu 6 cm wpisano w sposób symetryczny cztery przystające okręgi. Oblicz ich promień.
Trzy okręgi o promieniach 2, 4 i 6 są parami zewnętrznie styczne. Oblicz długość promienia okręgu zawierającego punkty styczności tych okręgów.
W kąt o mierze 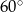 wpisano dwa okręgi styczne zewnętrznie. Promień mniejszego okręgu ma długość 1. Oblicz długość promienia drugiego okręgu.
wpisano dwa okręgi styczne zewnętrznie. Promień mniejszego okręgu ma długość 1. Oblicz długość promienia drugiego okręgu.
Okrąg dopisany do boku 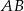 trójkąta
trójkąta 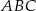 to okrąg, który jest jednocześnie styczny do tego boku, oraz do przedłużeń boków
to okrąg, który jest jednocześnie styczny do tego boku, oraz do przedłużeń boków 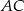 i
i 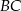 .
.
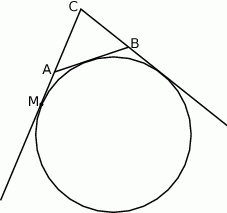
Wykaż, że jeżeli 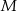 jest punktem styczności tego okręgu z przedłużeniem boku
jest punktem styczności tego okręgu z przedłużeniem boku 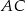 to długość odcinka
to długość odcinka 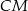 jest równa połowie obwodu trójkąta
jest równa połowie obwodu trójkąta 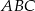 .
.
Przez punkty 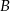 i
i 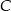 okręgu poprowadzono styczne, które przecięły się w punkcie
okręgu poprowadzono styczne, które przecięły się w punkcie 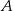 .
.
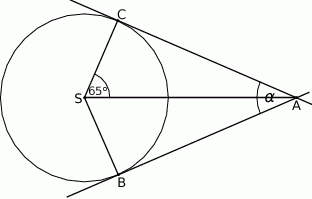
Oblicz miarę kąta 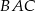 jeżeli
jeżeli 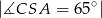 .
.
Wykaż, że stosunek pola kwadratu wpisanego w koło do pola tego koła jest mniejszy od  .
.
Wykaż, że stosunek pola kwadratu opisanego na kole do pola tego koła jest mniejszy od 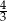 .
.
Dwa okręgi są styczne zewnętrznie, a odległość ich środków jest równa 19. Gdyby te okręgi były styczne wewnętrznie, to ta odległość wynosiłaby 5. Wyznacz długości promieni tych okręgów.
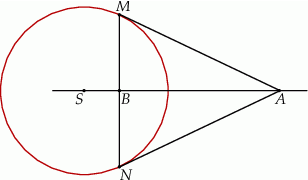
Na okręgu o promieniu  wybrano punkty
wybrano punkty 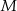 i
i 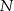 w ten sposób, że proste
w ten sposób, że proste 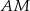 i
i 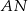 są styczne do okręgu. Punkt
są styczne do okręgu. Punkt 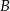 jest punktem wspólnym odcinka
jest punktem wspólnym odcinka 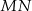 i prostej łączącej
i prostej łączącej 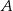 ze środkiem
ze środkiem 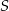 tego okręgu. Wykaż, że
tego okręgu. Wykaż, że 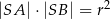 .
.
Środek okręgu leży w odległości 10 cm od cięciwy tego okręgu. Długość tej cięciwy jest o 22 cm większa od promienia tego okręgu. Oblicz promień tego okręgu.
Środek okręgu leży w odległości 8 cm od cięciwy tego okręgu. Długość tej cięciwy jest o 13 cm większa od promienia tego okręgu. Oblicz promień tego okręgu.
Trzy koła o promieniu 1 są parami styczne zewnętrznie. Oblicz pole obszaru zawartego między tymi kołami.
Ramiona kąta o mierze 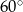 przecięto prostą
przecięto prostą 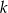 prostopadłą do jednego z ramion kąta i wpisano dwa koła styczne do obu ramion tego kąta i prostej
prostopadłą do jednego z ramion kąta i wpisano dwa koła styczne do obu ramion tego kąta i prostej 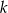 . Oblicz stosunek pól tych kół.
. Oblicz stosunek pól tych kół.
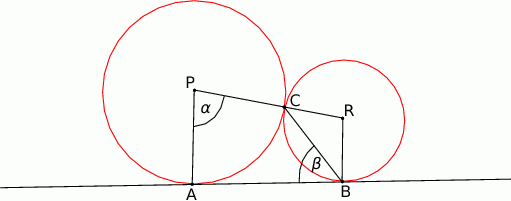
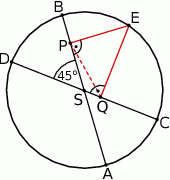
Wiedząc, że punkt 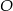 jest środkiem okręgu, oblicz miarę kąta
jest środkiem okręgu, oblicz miarę kąta  .
.
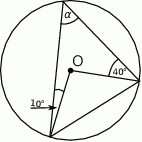
W wycinek koła o kącie 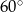 wpisano okrąg o promieniu 2 cm. Oblicz pole tego wycinka.
wpisano okrąg o promieniu 2 cm. Oblicz pole tego wycinka.
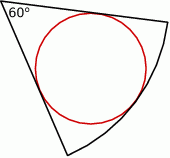
Z półokręgów budujemy krzywą (patrz rysunek). Pierwszy półokrąg ma promień długości 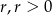 , a promień każdego następnego półokręgu stanowi
, a promień każdego następnego półokręgu stanowi  promienia poprzedniego. Niech
promienia poprzedniego. Niech  oznacza liczbę półokręgów tworzących tę krzywą. Udowodnij, że dla dowolnej liczby naturalnej dodatniej
oznacza liczbę półokręgów tworzących tę krzywą. Udowodnij, że dla dowolnej liczby naturalnej dodatniej  długość krzywej jest mniejsza od
długość krzywej jest mniejsza od 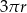 .
.

Na okręgu o środku 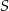 wybrano punkty
wybrano punkty 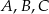 i
i 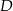 w ten sposób, że prosta
w ten sposób, że prosta 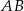 zawiera punkt
zawiera punkt 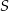 , a proste
, a proste 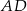 i
i 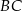 przecinają się w punkcie
przecinają się w punkcie 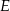 . Punkt
. Punkt 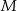 jest punktem wspólnym prostych
jest punktem wspólnym prostych 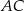 i
i 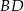 . Wykaż, że proste
. Wykaż, że proste 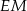 i
i 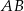 są prostopadłe.
są prostopadłe.
Dane są dwa okręgi o środkach w punktach 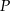 i
i 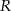 , styczne zewnętrznie w punkcie
, styczne zewnętrznie w punkcie 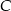 . Prosta
. Prosta 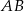 jest styczna do obu okręgów odpowiednio w punktach
jest styczna do obu okręgów odpowiednio w punktach 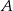 i
i 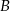 oraz
oraz 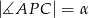 i
i 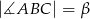 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 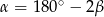 .
.
Dane są dwa okręgi o środkach w punktach 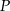 i
i 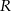 , styczne wewnętrznie w punkcie
, styczne wewnętrznie w punkcie 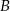 . Prosta
. Prosta 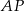 jest styczna do mniejszego okręgu w punkcie
jest styczna do mniejszego okręgu w punkcie 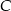 oraz
oraz 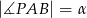 i
i 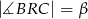 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 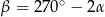 .
.
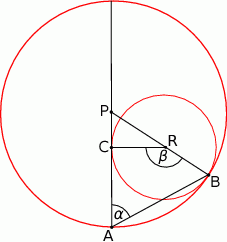
W okręgu o promieniu 6 średnice 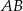 i
i 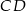 przecinają się pod kątem
przecinają się pod kątem 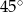 . Na okręgu tym wybrano punkt
. Na okręgu tym wybrano punkt 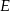 oraz skonstruowano jego rzuty
oraz skonstruowano jego rzuty 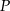 i
i 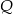 odpowiednio na średnice
odpowiednio na średnice 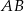 i
i 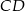 . Oblicz długość odcinka
. Oblicz długość odcinka 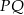 .
.
Na okręgu wybrano takich pięć różnych punktów: 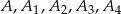 , że
, że
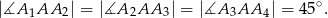
Udowodnij, że punkty 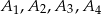 są wierzchołkami kwadratu.
są wierzchołkami kwadratu.
Dany jest okrąg 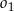 . Kreślimy cięciwę
. Kreślimy cięciwę 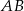 nieprzechodzącą przez środek okręgu
nieprzechodzącą przez środek okręgu 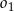 , a następnie rysujemy okrąg
, a następnie rysujemy okrąg 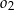 współśrodkowy z okręgiem
współśrodkowy z okręgiem 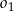 i styczny do cięciwy
i styczny do cięciwy 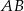 . Okręgi
. Okręgi 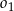 i
i 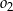 ograniczają pierścień kołowy. Uzasadnij, że pole pierścienia kołowego nie zależy od długości promienia okręgu
ograniczają pierścień kołowy. Uzasadnij, że pole pierścienia kołowego nie zależy od długości promienia okręgu 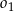 (zależy tylko od długości cięciwy
(zależy tylko od długości cięciwy 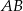 ).
).

