W okrąg wpisano trapez równoramienny 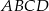 , którego podstawy mają długości:
, którego podstawy mają długości: 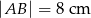 ,
, 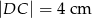 . Styczna do okręgu w punkcie
. Styczna do okręgu w punkcie 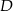 przecina prostą
przecina prostą 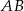 w punkcie
w punkcie 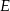 (rys). Wiedząc, że
(rys). Wiedząc, że 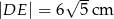 oblicz promień okręgu opisanego na trapezie
oblicz promień okręgu opisanego na trapezie 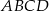 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W okrąg wpisano trapez równoramienny 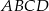 , którego podstawy mają długości:
, którego podstawy mają długości: 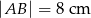 ,
, 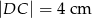 . Styczna do okręgu w punkcie
. Styczna do okręgu w punkcie 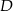 przecina prostą
przecina prostą 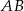 w punkcie
w punkcie 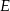 (rys). Wiedząc, że
(rys). Wiedząc, że 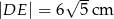 oblicz promień okręgu opisanego na trapezie
oblicz promień okręgu opisanego na trapezie 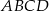 .
.

Na trapezie opisano okrąg o promieniu długości 25 cm. Dłuższa podstawa trapezu jest średnicą tego okręgu. Wiedząc że przekątna tego trapezu ma długość 40 cm, oblicz obwód tego trapezu.
Trapez 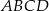 (
(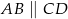 ,
, 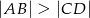 ) jest wpisany w okrąg o promieniu długości
) jest wpisany w okrąg o promieniu długości 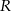 . Wiadomo że kąt ostry trapezu ma miarę
. Wiadomo że kąt ostry trapezu ma miarę  zaś
zaś 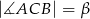 , gdzie
, gdzie 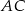 jest przekątną trapezu. Oblicz długość
jest przekątną trapezu. Oblicz długość  dłuższej podstawy tego trapezu oraz długość
dłuższej podstawy tego trapezu oraz długość 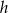 jego wysokości.
jego wysokości.
Oblicz promień okręgu opisanego na trapezie równoramiennym, w którym sinus kąta ostrego jest równy  , a przekątna ma długość 12.
, a przekątna ma długość 12.
Podstawy trapezu równoramiennego mają długości 3 i 5, a jego ramię ma długość 2. Oblicz promień okręgu opisanego na tym trapezie.
W okrąg wpisano trapez równoramienny 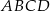 w ten sposób, że podstawa
w ten sposób, że podstawa 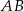 jest średnicą tego okręgu. Ramię trapezu ma długość 10, a jego przekątna jest o 11 dłuższa od promienia okręgu. Oblicz wysokość tego trapezu.
jest średnicą tego okręgu. Ramię trapezu ma długość 10, a jego przekątna jest o 11 dłuższa od promienia okręgu. Oblicz wysokość tego trapezu.
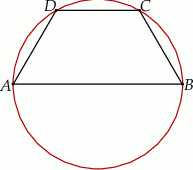
Na trapezie 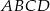 można opisać okrąg. Jedna z jego podstaw jest dwa razy dłuższa od drugiej, a przekątna dzieli kąt przy dłuższej podstawie na połowy. Oblicz długości boków trapezu wiedząc, że jego ple jest równe
można opisać okrąg. Jedna z jego podstaw jest dwa razy dłuższa od drugiej, a przekątna dzieli kąt przy dłuższej podstawie na połowy. Oblicz długości boków trapezu wiedząc, że jego ple jest równe 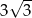 .
.
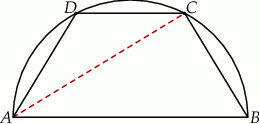
W półkole o promieniu  wpisano trapez równoramienny o krótszej podstawie długości
wpisano trapez równoramienny o krótszej podstawie długości  . Oblicz długość przekątnej trapezu.
. Oblicz długość przekątnej trapezu.
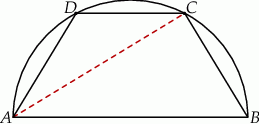
W półkole o promieniu  wpisano trapez równoramienny o przekątnej długości
wpisano trapez równoramienny o przekątnej długości 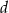 . Oblicz długość krótszej podstawy trapezu.
. Oblicz długość krótszej podstawy trapezu.