Napisz równanie stycznej do krzywej 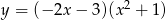 w punkcie
w punkcie 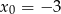 .
.
/Szkoła średnia/Funkcje - wykresy/Styczna do wykresu
Napisz równanie stycznej do krzywej 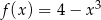 wiedząc, że jest ona równoległa do prostej
wiedząc, że jest ona równoległa do prostej 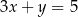 .
.
Funkcja 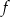 określona jest wzorem
określona jest wzorem 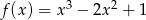 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 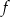 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 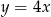 .
.
Funkcja 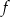 określona jest wzorem
określona jest wzorem 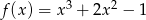 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 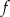 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 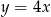 .
.
Funkcja 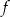 jest określona wzorem
jest określona wzorem 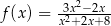 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Punkt
. Punkt 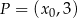 należy do wykresu funkcji
należy do wykresu funkcji 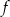 . Oblicz
. Oblicz 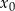 oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji 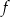 w punkcie
w punkcie 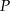 .
.
Funkcja 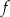 jest określona wzorem
jest określona wzorem 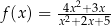 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Punkt
. Punkt 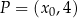 należy do wykresu funkcji
należy do wykresu funkcji 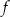 . Oblicz
. Oblicz 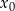 oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji 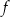 w punkcie
w punkcie 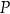 .
.
Wyznacz wszystkie wartości parametru  , dla których prosta o równaniu
, dla których prosta o równaniu 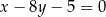 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 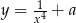 .
.
Wyznacz wszystkie styczne do wykresu funkcji 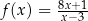 , które razem z osiami układu współrzędnych ograniczają trójkąt równoramienny.
, które razem z osiami układu współrzędnych ograniczają trójkąt równoramienny.
Z punktu 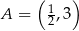 poprowadzono styczne do wykresu funkcji
poprowadzono styczne do wykresu funkcji 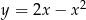 . Wyznacz równia tych stycznych.
. Wyznacz równia tych stycznych.
Oblicz współczynnik kierunkowy stycznej do wykresu funkcji 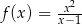 , określonej dla każdej liczby rzeczywistej
, określonej dla każdej liczby rzeczywistej 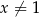 , poprowadzonej w punkcie
, poprowadzonej w punkcie 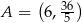 tego wykresu.
tego wykresu.
Oblicz współczynnik kierunkowy stycznej do wykresu funkcji 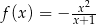 , określonej dla każdej liczby rzeczywistej
, określonej dla każdej liczby rzeczywistej 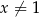 , poprowadzonej w punkcie
, poprowadzonej w punkcie 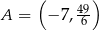 tego wykresu.
tego wykresu.
Dana jest funkcja 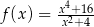 określona dla
określona dla 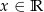 . Wyznacz równania stycznych do wykresu funkcji
. Wyznacz równania stycznych do wykresu funkcji 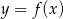 w punktach o rzędnej
w punktach o rzędnej 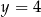 .
.
Dla jakich wartości parametru 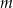 prosta
prosta 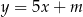 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 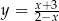 ?
?
Dla jakich wartości parametru 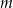 prosta
prosta 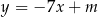 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 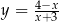 ?
?
Wyznacz pole trójkąta, którego dwa boki zawierają się w asymptotach wykresu funkcji 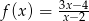 , a trzeci bok zawiera się w stycznej do wykresu tej funkcji w punkcie
, a trzeci bok zawiera się w stycznej do wykresu tej funkcji w punkcie 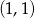 .
.
Funkcja 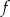 jest określona wzorem
jest określona wzorem 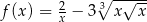 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 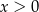 . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie 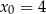 .
.
Prostą o równaniu 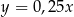 przesunięto o wektor postaci
przesunięto o wektor postaci ![[1,m ]](https://img.zadania.info/zad/2734711/HzadT1x.gif) w taki sposób, że przesunięta prosta jest styczna do wykresu funkcji
w taki sposób, że przesunięta prosta jest styczna do wykresu funkcji 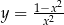 . Oblicz wartość
. Oblicz wartość 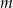 .
.
Wyznacz równania wszystkich stycznych do wykresu funkcji 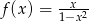 ,
, 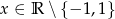 nachylonych do osi
nachylonych do osi 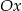 pod kątem
pod kątem 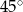 .
.
Funkcja 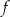 jest określona wzorem
jest określona wzorem 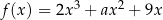 dla każdego
dla każdego 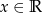 , i ustalonej liczby rzeczywistej
, i ustalonej liczby rzeczywistej  . Prosta
. Prosta 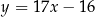 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 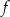 . Oblicz
. Oblicz  .
.
Oblicz pole trójkąta ograniczonego osią 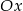 oraz stycznymi do wykresu funkcji
oraz stycznymi do wykresu funkcji 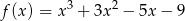 poprowadzonymi w punktach
poprowadzonymi w punktach 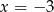 i
i 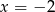 .
.
Napisz równanie stycznych do wykresu funkcji 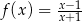 i równoległych do prostej o równaniu
i równoległych do prostej o równaniu 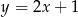 .
.
Napisz równanie stycznych do wykresu funkcji 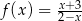 i równoległych do prostej o równaniu
i równoległych do prostej o równaniu 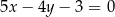 .
.
Oblicz pole trójkąta ograniczonego przez osie układu współrzędnych oraz styczną do wykresu funkcji 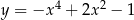 w punkcie
w punkcie 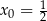 .
.
Funkcja 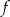 jest wielomianem stopnia 3, a jej wykres znajduje się powyżej osi
jest wielomianem stopnia 3, a jej wykres znajduje się powyżej osi 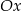 na zbiorze
na zbiorze 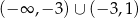 . Wyznacz równanie stycznej do wykresu funkcji
. Wyznacz równanie stycznej do wykresu funkcji 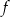 w punkcie
w punkcie 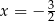 jeżeli wiadomo, że styczna ta jest równoległa do prostej
jeżeli wiadomo, że styczna ta jest równoległa do prostej 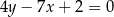 .
.
Funkcja 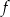 jest wielomianem stopnia 3, a jej wykres jest styczny do prostej
jest wielomianem stopnia 3, a jej wykres jest styczny do prostej 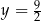 w punkcie o odciętej
w punkcie o odciętej 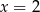 oraz jest styczny do prostej
oraz jest styczny do prostej 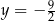 w punkcie o odciętej
w punkcie o odciętej 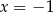 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 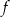 .
.
Punkt 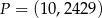 leży na paraboli o równaniu
leży na paraboli o równaniu 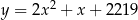 . Prosta o równaniu kierunkowym
. Prosta o równaniu kierunkowym 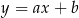 jest styczna do tej paraboli w punkcie
jest styczna do tej paraboli w punkcie 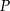 . Oblicz współczynnik
. Oblicz współczynnik 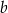 .
.
Punkt 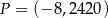 leży na paraboli o równaniu
leży na paraboli o równaniu 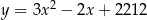 . Prosta o równaniu kierunkowym
. Prosta o równaniu kierunkowym 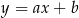 jest styczna do tej paraboli w punkcie
jest styczna do tej paraboli w punkcie 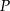 . Oblicz współczynnik
. Oblicz współczynnik 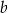 .
.

