Wykaż, że wszystkie trójkąty ograniczone osiami układu współrzędnych i dowolną styczną do wykresu funkcji 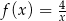 , określonej dla
, określonej dla 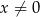 , mają równe pola.
, mają równe pola.
/Szkoła średnia/Funkcje - wykresy/Styczna do wykresu
Funkcja 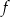 określona jest wzorem
określona jest wzorem 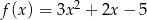 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 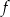 , które przechodzą przez punkt
, które przechodzą przez punkt 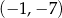 .
.
Funkcja 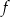 określona jest wzorem
określona jest wzorem 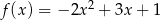 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 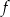 , które przechodzą przez punkt
, które przechodzą przez punkt 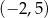 .
.
Napisz równanie stycznej do krzywej 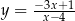 w punkcie
w punkcie 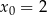 .
.
Funkcja 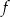 jest określona wzorem
jest określona wzorem 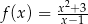 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 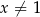 . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie 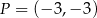 .
.
Napisz równanie stycznej do krzywej 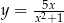 w punkcie
w punkcie 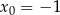 .
.
Funkcja 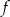 jest określona wzorem
jest określona wzorem 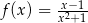 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie 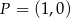 .
.
Funkcja 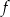 jest określona wzorem
jest określona wzorem 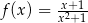 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie 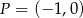 .
.
Funkcja 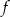 jest określona wzorem
jest określona wzorem 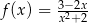 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie o odciętej
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie o odciętej 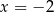 .
.
Funkcja 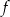 jest określona wzorem
jest określona wzorem 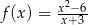 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 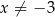 . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie 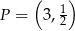 .
.
Funkcja 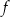 jest określona wzorem
jest określona wzorem
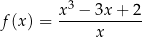
dla każdej liczby rzeczywistej  różnej od zera. W kartezjańskim układzie współrzędnych
różnej od zera. W kartezjańskim układzie współrzędnych 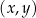 punkt
punkt 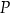 , o pierwszej współrzędnej równej 2, należy do wykresu funkcji
, o pierwszej współrzędnej równej 2, należy do wykresu funkcji 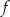 . Prosta o równaniu
. Prosta o równaniu 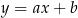 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 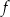 w punkcie
w punkcie 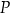 . Oblicz współczynniki
. Oblicz współczynniki  oraz
oraz 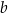 w równaniu tej stycznej.
w równaniu tej stycznej.
Funkcja 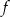 jest określona wzorem
jest określona wzorem 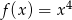 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie prostej stycznej do wykresu funkcji
. Wyznacz równanie prostej stycznej do wykresu funkcji 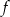 , która jest równoległa do prostej
, która jest równoległa do prostej 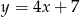 .
.
Funkcja 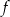 jest określona wzorem
jest określona wzorem 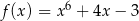 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie prostej stycznej do wykresu funkcji
. Wyznacz równanie prostej stycznej do wykresu funkcji 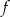 , która jest równoległa do prostej
, która jest równoległa do prostej 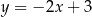 .
.
Funkcja 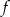 jest określona wzorem
jest określona wzorem 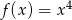 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie prostej stycznej do wykresu funkcji
. Wyznacz równanie prostej stycznej do wykresu funkcji 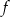 , która jest równoległa do prostej
, która jest równoległa do prostej 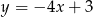 .
.
Funkcja 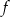 jest określona wzorem
jest określona wzorem 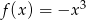 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania prostych stycznych do wykresu funkcji
. Wyznacz równania prostych stycznych do wykresu funkcji 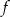 , które są równoległe do prostej
, które są równoległe do prostej 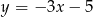 .
.
Funkcja 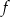 jest określona wzorem
jest określona wzorem 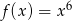 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie prostej stycznej do wykresu funkcji
. Wyznacz równanie prostej stycznej do wykresu funkcji 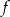 , która jest równoległa do prostej
, która jest równoległa do prostej 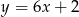 .
.
Funkcja 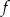 jest określona wzorem
jest określona wzorem 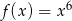 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie prostej stycznej do wykresu funkcji
. Wyznacz równanie prostej stycznej do wykresu funkcji 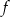 , która jest równoległa do prostej
, która jest równoległa do prostej 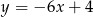 .
.
Napisz równanie stycznej do wykresu funkcji 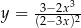 w punkcie
w punkcie 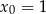 .
.
Napisz równanie stycznej do wykresu funkcji 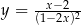 w punkcie
w punkcie 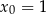 .
.
Funkcja 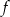 określona jest wzorem
określona jest wzorem 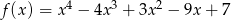 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 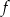 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 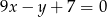 .
.
Funkcja 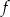 określona jest wzorem
określona jest wzorem 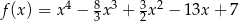 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 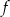 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 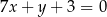 .
.
Rozważamy wszystkie proste na płaszczyźnie, które są jednocześnie styczne do wykresu funkcji homograficznej 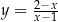 oraz do okręgu o równaniu
oraz do okręgu o równaniu 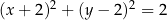 . Wyznacz równania tych spośród rozważanych prostych, których współczynniki kierunkowe są liczbami wymiernymi.
. Wyznacz równania tych spośród rozważanych prostych, których współczynniki kierunkowe są liczbami wymiernymi.
Oblicz pole trójkąta utworzonego przez prostą 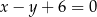 , oś
, oś 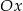 oraz styczną do wykresu funkcji
oraz styczną do wykresu funkcji 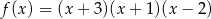 w punkcie o pierwszej współrzędnej
w punkcie o pierwszej współrzędnej 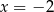 .
.
Wyznacz wszystkie proste, które są jednocześnie styczne do paraboli 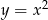 oraz okręgu o równaniu
oraz okręgu o równaniu 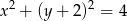 .
.
Wyznacz wzór funkcji kwadratowej 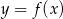 wiedząc, że jest on styczny do prostej
wiedząc, że jest on styczny do prostej 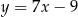 w punkcie
w punkcie 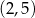 oraz przechodzi przez punkt
oraz przechodzi przez punkt 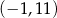 .
.
Wyznacz wzór funkcji kwadratowej 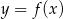 wiedząc, że jest on styczny do prostej
wiedząc, że jest on styczny do prostej 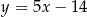 w punkcie
w punkcie 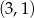 oraz przechodzi przez punkt
oraz przechodzi przez punkt 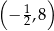 .
.
Wyznacz wszystkie wartości parametru  , dla których prosta
, dla których prosta 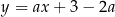 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 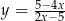 w punkcie o drugiej współrzędnej równej 3.
w punkcie o drugiej współrzędnej równej 3.
Prosta 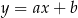 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 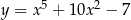 . Wykaż, że
. Wykaż, że 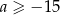 .
.
Funkcja 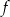 określona jest wzorem
określona jest wzorem 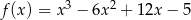 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 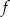 , które przechodzą przez punkt
, które przechodzą przez punkt 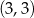 .
.
Prosta postaci 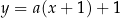 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 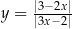 w punkcie
w punkcie 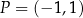 . Oblicz
. Oblicz  .
.
Dana jest funkcja 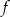 określona wzorem
określona wzorem 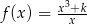 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 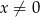 . Oblicz wartość
. Oblicz wartość 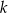 , dla której prosta o równaniu
, dla której prosta o równaniu 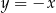 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 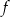 .
.
Dana jest funkcja 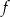 określona wzorem
określona wzorem 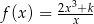 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 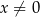 . Oblicz wartość
. Oblicz wartość 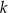 , dla której prosta o równaniu
, dla której prosta o równaniu 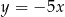 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 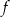 .
.
Styczna do paraboli o równaniu 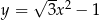 w punkcie
w punkcie 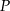 przecina prostą o równaniu
przecina prostą o równaniu 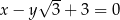 pod kątem
pod kątem 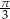 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 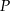 .
.
Dana jest funkcja kwadratowa 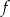 określona wzorem
określona wzorem 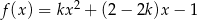 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  i
i 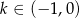 . Wyznacz równania dwóch prostopadłych stycznych do wykresu funkcji
. Wyznacz równania dwóch prostopadłych stycznych do wykresu funkcji 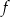 poprowadzonych w punktach, których pierwsze współrzędne różnią się o 2, jeżeli wiadomo, że funkcja
poprowadzonych w punktach, których pierwsze współrzędne różnią się o 2, jeżeli wiadomo, że funkcja 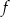 ma maksimum lokalne równe
ma maksimum lokalne równe  .
.
Punkt 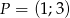 należy do wykresu funkcji
należy do wykresu funkcji 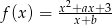 , gdzie
, gdzie 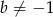 . Styczna do wykresu danej funkcji, poprowadzona w punkcie
. Styczna do wykresu danej funkcji, poprowadzona w punkcie 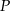 , jest prostopadła do prostej o równaniu
, jest prostopadła do prostej o równaniu 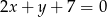 . Oblicz współczynniki
. Oblicz współczynniki  i
i 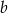 oraz napisz równanie tej stycznej.
oraz napisz równanie tej stycznej.
Punkt 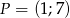 należy do wykresu funkcji
należy do wykresu funkcji 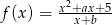 , gdzie
, gdzie 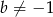 . Styczna do wykresu danej funkcji, poprowadzona w punkcie
. Styczna do wykresu danej funkcji, poprowadzona w punkcie 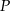 , jest prostopadła do prostej o równaniu
, jest prostopadła do prostej o równaniu 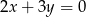 . Oblicz współczynniki
. Oblicz współczynniki  i
i 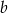 oraz napisz równanie tej stycznej.
oraz napisz równanie tej stycznej.
Wyznacz równanie stycznej do wykresu funkcji 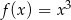 , która przecina oś
, która przecina oś 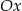 w jednym punkcie:
w jednym punkcie: 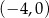 .
.
Wyznacz wszystkie wartości parametru 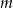 , dla których prosta
, dla których prosta 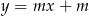 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 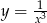 .
.

