Wielomian 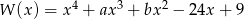 jest kwadratem wielomianu
jest kwadratem wielomianu 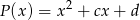 . Oblicz
. Oblicz  oraz
oraz 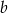 .
.
/Szkoła średnia/Funkcje/Wielomiany/Stopnia 4
Przedstaw wielomian 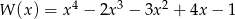 w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i takich, że współczynniki przy drugich potęgach są równe jeden.
w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i takich, że współczynniki przy drugich potęgach są równe jeden.
Wielomiany 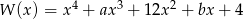 oraz
oraz 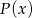 są wielomianami o współczynnikach całkowitych, przy czym
są wielomianami o współczynnikach całkowitych, przy czym ![W (x ) = [P (x)]2](https://img.zadania.info/zad/3139795/HzadT2x.gif) . Wyznacz wszystkie możliwe wartości
. Wyznacz wszystkie możliwe wartości  i
i 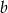 .
.
Wielomiany 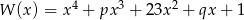 oraz
oraz 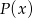 są wielomianami o współczynnikach całkowitych, przy czym
są wielomianami o współczynnikach całkowitych, przy czym ![W (x ) = [P (x)]2](https://img.zadania.info/zad/1984880/HzadT2x.gif) . Wyznacz wszystkie możliwe wartości
. Wyznacz wszystkie możliwe wartości 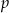 i
i 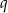 .
.
Funkcja 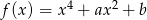 przyjmuje wartość 1 dla czterech argumentów:
przyjmuje wartość 1 dla czterech argumentów:
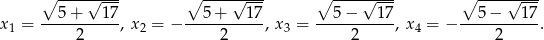
Oblicz najmniejszą wartość tej funkcji.
Zbadaj, czy istnieje taka wartość współczynnika  , dla której wielomiany
, dla której wielomiany 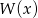 i
i ![[Q (x)]2](https://img.zadania.info/zad/4602131/HzadT2x.gif) są równe, jeśli
są równe, jeśli 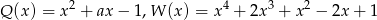 .
.
Rozłóż na czynniki drugiego stopnia wielomian 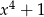 .
.
Rozłóż wielomian 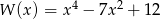 na czynniki liniowe. Podaj niewymierne pierwiastki tego wielomianu.
na czynniki liniowe. Podaj niewymierne pierwiastki tego wielomianu.
Przedstaw wielomian 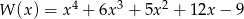 w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i tak, aby współczynniki przy drugich potęgach były równe jeden.
w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i tak, aby współczynniki przy drugich potęgach były równe jeden.

