Dany jest trapez prostokątny 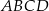 o podstawach
o podstawach 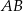 i
i 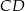 oraz wysokości
oraz wysokości 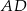 . Dwusieczna kąta
. Dwusieczna kąta 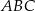 przecina ramię
przecina ramię 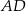 w punkcie
w punkcie 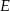 oraz dwusieczną kąta
oraz dwusieczną kąta 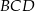 w punkcie
w punkcie 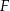 (zobacz rysunek).
(zobacz rysunek).
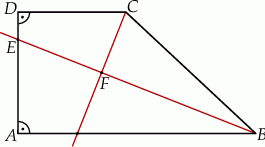
Wykaż, że w czworokącie 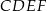 sumy miar przeciwległych kątów są sobie równe.
sumy miar przeciwległych kątów są sobie równe.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest trapez prostokątny 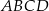 o podstawach
o podstawach 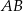 i
i 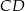 oraz wysokości
oraz wysokości 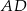 . Dwusieczna kąta
. Dwusieczna kąta 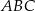 przecina ramię
przecina ramię 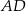 w punkcie
w punkcie 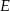 oraz dwusieczną kąta
oraz dwusieczną kąta 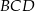 w punkcie
w punkcie 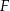 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że w czworokącie 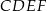 sumy miar przeciwległych kątów są sobie równe.
sumy miar przeciwległych kątów są sobie równe.
Znaleźć kąt ostry rombu, jeżeli wiadomo, że jego pole jest równe 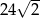 , a promień okręgu w niego wpisanego równy
, a promień okręgu w niego wpisanego równy 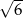 .
.
Wykaż, że stosunek długości promienia okręgu opisanego na kwadracie do długości promienia wpisanego w ten kwadrat jest równy 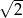 .
.
Wykaż, że stosunek długości promienia okręgu wpisanego w kwadrat do długości promienia okręgu opisanego na kwadracie jest równy 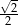 .
.
Oblicz miarę kąta:
Punkty 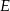 i
i 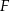 są środkami boków
są środkami boków 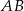 i
i 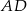 deltoidu
deltoidu 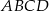 . Pole trójkąta
. Pole trójkąta 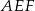 jest równe 3. Oblicz pole deltoidu
jest równe 3. Oblicz pole deltoidu 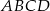 .
.
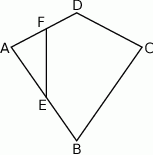
W trójkącie 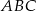 dwusieczna kąta
dwusieczna kąta 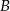 przecina bok
przecina bok 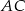 w punkcie
w punkcie 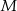 . Przez punkt
. Przez punkt 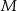 prowadzimy prostą równoległą do
prowadzimy prostą równoległą do 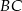 , przecinającą bok
, przecinającą bok 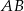 w punkcie
w punkcie 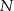 (rys.). Udowodnij, że
(rys.). Udowodnij, że 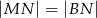 .
.
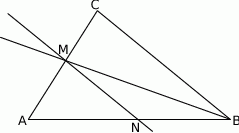
W trójkącie 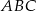 dwusieczna kąta
dwusieczna kąta 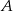 przecina bok
przecina bok 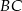 w punkcie
w punkcie 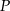 . Przez punkt
. Przez punkt 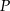 prowadzimy prostą równoległą do
prowadzimy prostą równoległą do 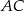 , przecinającą bok
, przecinającą bok 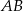 w punkcie
w punkcie 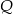 (rys.). Udowodnij, że
(rys.). Udowodnij, że 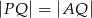 .
.
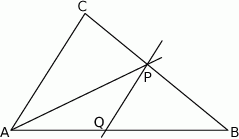
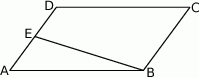
W trapezie prostokątnym krótsza przekątna dzieli go na trójkąt prostokątny i trójkąt równoboczny. Dłuższa podstawa trapezu jest równa 6. Oblicz obwód tego trapezu.
W trapezie prostokątnym krótsza przekątna ma długość ramienia trapezu i dzieli go na dwa trójkąty prostokątne. Dłuższa podstawa trapezu jest równa 6. Oblicz obwód tego trapezu.
Liczby 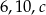 są długościami boków trójkąta prostokątnego. Oblicz
są długościami boków trójkąta prostokątnego. Oblicz  .
.
W prostokącie przekątna o długości 1,53 cm tworzy z dłuższym bokiem kąt o mierze 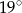 . Oblicz z dokładnością do
. Oblicz z dokładnością do 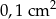 pole prostokąta.
pole prostokąta.
Punkty 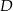 i
i 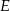 są takimi punktami przeciwprostokątnej
są takimi punktami przeciwprostokątnej 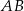 trójkąta prostokątnego
trójkąta prostokątnego 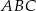 , że
, że 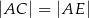 i
i 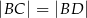 . Wykaż, że
. Wykaż, że 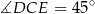 .
.
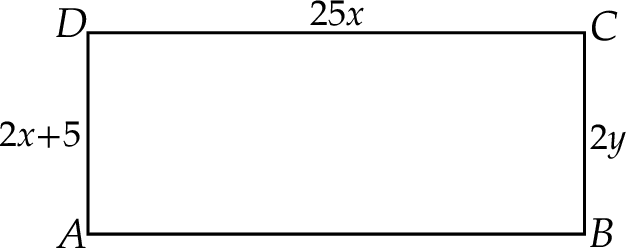
Wyznacz pole narysowanego prostokąta, jeżeli 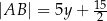 .
.
Przez punkty 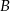 i
i 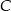 okręgu poprowadzono styczne, które przecięły się w punkcie
okręgu poprowadzono styczne, które przecięły się w punkcie 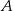 .
.
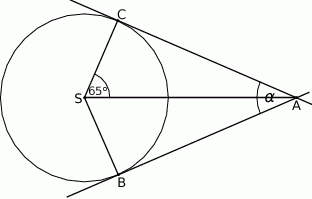
Oblicz miarę kąta 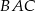 jeżeli
jeżeli 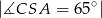 .
.
Wykaż, że stosunek pola kwadratu wpisanego w koło do pola tego koła jest mniejszy od  .
.
Wykaż, że stosunek pola kwadratu opisanego na kole do pola tego koła jest mniejszy od 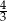 .
.
Dwa okręgi są styczne zewnętrznie, a odległość ich środków jest równa 19. Gdyby te okręgi były styczne wewnętrznie, to ta odległość wynosiłaby 5. Wyznacz długości promieni tych okręgów.
Pola dwóch kwadratów różnią się o 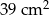 . Przekątna jednego z nich jest dłuższa o
. Przekątna jednego z nich jest dłuższa o 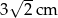 od przekątnej drugiego. Oblicz długość boku każdego kwadratu.
od przekątnej drugiego. Oblicz długość boku każdego kwadratu.
W kwadrat o boku 2 wpisano drugi kwadrat w ten sposób, że bok wpisanego kwadratu tworzy z bokiem danego kąt 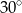 . Oblicz długość krótszego z odcinków łączących wierzchołki tych kwadratów.
. Oblicz długość krótszego z odcinków łączących wierzchołki tych kwadratów.
Punkt 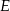 jest środkiem boku
jest środkiem boku 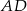 równoległoboku
równoległoboku 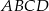 . Pole trójkąta
. Pole trójkąta 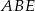 jest równe 2. Oblicz pole równoległoboku.
jest równe 2. Oblicz pole równoległoboku.
Sprawdź, czy trójkąt o bokach: 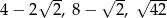 jest trójkątem prostokątnym.
jest trójkątem prostokątnym.
Sprawdź, czy trójkąt o bokach: 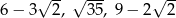 jest trójkątem prostokątnym.
jest trójkątem prostokątnym.
Ile jest trójkątów o obwodzie równym 19, w których długości boków wyrażone są liczbami całkowitymi. Wymień je.
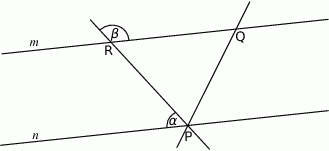
Proste 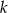 i
i 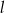 na poniższym rysunku są równoległe oraz
na poniższym rysunku są równoległe oraz 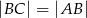 . Kąt
. Kąt 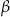 jest o
jest o 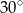 większy od podwojonego kąta
większy od podwojonego kąta  . Oblicz miarę
. Oblicz miarę 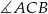 .
.
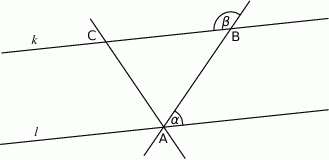
Proste 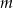 i
i  na poniższym rysunku są równoległe oraz
na poniższym rysunku są równoległe oraz 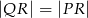 . Kąt
. Kąt 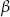 jest o
jest o 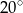 mniejszy od potrojonego kąta
mniejszy od potrojonego kąta  . Oblicz miarę
. Oblicz miarę 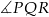 .
.