Odcinki 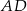 i
i 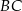 przecinają się w punkcie
przecinają się w punkcie 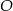 . W trójkątach
. W trójkątach 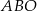 i
i 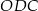 zachodzą związki:
zachodzą związki: 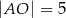 ,
, 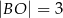 ,
, 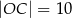 ,
, 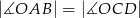 (zobacz rysunek).
(zobacz rysunek).
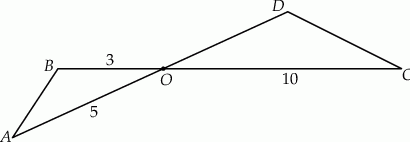
Oblicz długość boku 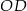 trójkąta
trójkąta 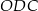 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Odcinki 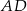 i
i 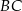 przecinają się w punkcie
przecinają się w punkcie 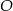 . W trójkątach
. W trójkątach 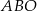 i
i 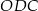 zachodzą związki:
zachodzą związki: 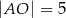 ,
, 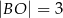 ,
, 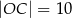 ,
, 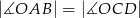 (zobacz rysunek).
(zobacz rysunek).

Oblicz długość boku 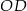 trójkąta
trójkąta 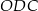 .
.
Odcinki 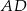 i
i 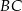 przecinają się w punkcie
przecinają się w punkcie 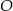 . W trójkątach
. W trójkątach 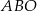 i
i 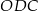 zachodzą związki:
zachodzą związki: 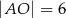 ,
, 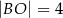 ,
, 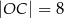 ,
, 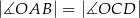 (zobacz rysunek).
(zobacz rysunek).
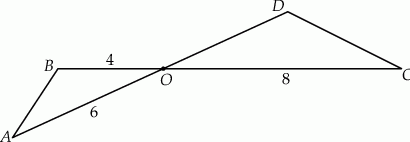
Oblicz długość boku 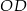 trójkąta
trójkąta 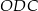 .
.
Proste 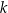 i
i 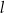 przecinają się w punkcie
przecinają się w punkcie 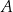 . Proste
. Proste 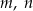 i
i  są wzajemnie równoległe i przecinają obie proste
są wzajemnie równoległe i przecinają obie proste 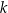 i
i 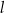 w punktach
w punktach 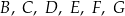 (zobacz rysunek poniżej), w taki sposób, że:
(zobacz rysunek poniżej), w taki sposób, że: 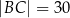 ,
, 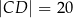 ,
, 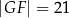 .
.
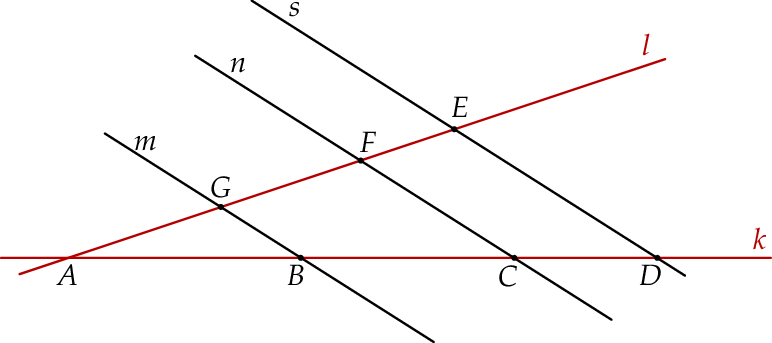
Oblicz długość odcinka 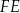 .
.
Wewnątrz kąta o mierze 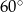 leży punkt
leży punkt 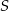 . Odległość tego punktu od ramion kąta wynosi odpowiednio
. Odległość tego punktu od ramion kąta wynosi odpowiednio 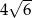 i
i 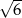 . Oblicz odległość tego punktu od wierzchołka kąta.
. Oblicz odległość tego punktu od wierzchołka kąta.
Punkty 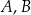 należą do jednego ramienia kąta o wierzchołku
należą do jednego ramienia kąta o wierzchołku 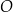 , a punkty
, a punkty 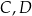 należą do jego drugiego ramienia i wiadomo, że
należą do jego drugiego ramienia i wiadomo, że 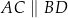 . Wyznacz
. Wyznacz 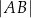 , jeśli wiadomo, że
, jeśli wiadomo, że 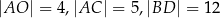 .
.
Proste 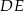 i
i 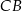 oraz
oraz 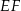 i
i 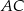 są równoległe. Oblicz długość odcinka
są równoległe. Oblicz długość odcinka 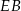 , jeżeli
, jeżeli 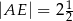 ,
, 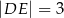 oraz
oraz 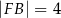 .
.
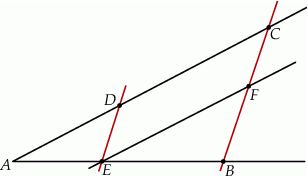
Proste 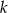 i
i 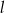 na poniższym rysunku są równoległe oraz
na poniższym rysunku są równoległe oraz 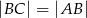 . Kąt
. Kąt 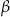 jest o
jest o 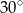 większy od podwojonego kąta
większy od podwojonego kąta  . Oblicz miarę
. Oblicz miarę 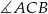 .
.
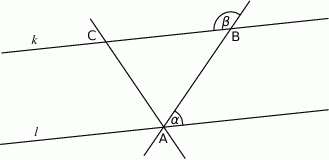
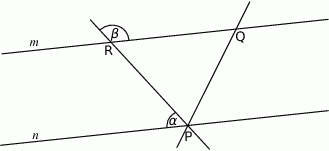
Proste 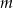 i
i  na poniższym rysunku są równoległe oraz
na poniższym rysunku są równoległe oraz 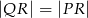 . Kąt
. Kąt 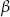 jest o
jest o 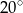 mniejszy od potrojonego kąta
mniejszy od potrojonego kąta  . Oblicz miarę
. Oblicz miarę 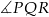 .
.
Do obszaru kąta ostrego o mierze  należy punkt
należy punkt 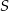 , którego odległości od ramion kąta są równe
, którego odległości od ramion kąta są równe  i
i 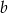 . Oblicz odległość punktu
. Oblicz odległość punktu 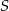 od wierzchołka kąta.
od wierzchołka kąta.
