Ze zbioru liczb 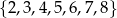 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 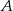 polegającego na wylosowaniu liczb, z których pierwsza jest o 2 mniejsza od drugiej.
polegającego na wylosowaniu liczb, z których pierwsza jest o 2 mniejsza od drugiej.
/Szkoła średnia/Prawdopodobieństwo/Z definicji
Ze zbioru liczb 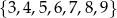 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 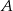 polegającego na wylosowaniu liczb, z których pierwsza jest o 3 większa od drugiej.
polegającego na wylosowaniu liczb, z których pierwsza jest o 3 większa od drugiej.
Ze zbioru sześciu liczb 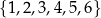 losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia
losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia 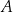 polegającego na tym, że pierwsza wylosowana liczba będzie większa od drugiej wylosowanej liczby.
polegającego na tym, że pierwsza wylosowana liczba będzie większa od drugiej wylosowanej liczby.
Na osi liczbowej każde dwie spośród 1000 kolejnych liczb naturalnych 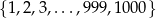 połączono odcinkiem. Następnie wybrano losowo jeden z tych odcinków. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że do wylosowanego odcinka należy liczba 307 (może też być jednym z jego końców). Wynik podaj w postaci ułamka nieskracalnego.
połączono odcinkiem. Następnie wybrano losowo jeden z tych odcinków. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że do wylosowanego odcinka należy liczba 307 (może też być jednym z jego końców). Wynik podaj w postaci ułamka nieskracalnego.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 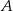 polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym cyfrę dziesiątek, która należy do zbioru
polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym cyfrę dziesiątek, która należy do zbioru 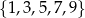 , i jednocześnie cyfrę jedności, która należy do zbioru
, i jednocześnie cyfrę jedności, która należy do zbioru 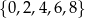 .
.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 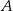 polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym nieparzystą cyfrę jedności, oraz parzystą cyfrę dziesiątek.
polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym nieparzystą cyfrę jedności, oraz parzystą cyfrę dziesiątek.
Ze zbioru 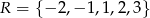 losujemy najpierw jedną liczbę i oznaczamy ją jako
losujemy najpierw jedną liczbę i oznaczamy ją jako  . Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako
. Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako 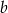 . Liczby
. Liczby  i
i 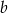 są współczynnikami funkcji kwadratowej
są współczynnikami funkcji kwadratowej 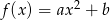 . Oblicz prawdopodobieństwo zdarzenia:
. Oblicz prawdopodobieństwo zdarzenia:
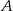 – funkcja
– funkcja 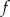 jest malejąca w zbiorze
jest malejąca w zbiorze 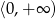 ,
, 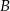 – funkcja
– funkcja 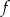 ma dwa różne miejsca zerowe.
ma dwa różne miejsca zerowe.
Ze zbioru 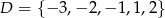 losujemy najpierw jedną liczbę i oznaczamy ją jako
losujemy najpierw jedną liczbę i oznaczamy ją jako  . Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako
. Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako 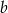 . Liczby
. Liczby  i
i 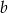 są współczynnikami funkcji kwadratowej
są współczynnikami funkcji kwadratowej 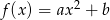 . Oblicz prawdopodobieństwo zdarzenia:
. Oblicz prawdopodobieństwo zdarzenia:
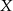 – funkcja
– funkcja 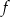 jest malejąca w zbiorze
jest malejąca w zbiorze 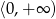 ,
, 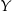 – funkcja
– funkcja 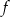 ma dwa różne miejsca zerowe.
ma dwa różne miejsca zerowe.
Ze zbioru liczb: 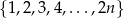 , gdzie
, gdzie 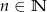 i
i 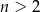 losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech
losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech 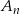 oznacza zdarzenie: iloczyn wylosowanych liczb jest liczbą nieparzystą, a
oznacza zdarzenie: iloczyn wylosowanych liczb jest liczbą nieparzystą, a 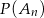 prawdopodobieństwo zajścia zdarzenia
prawdopodobieństwo zajścia zdarzenia 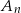 . Oblicz:
. Oblicz: 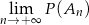 .
.
W fabryce zainstalowano 3 urządzenia 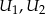 i
i 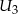 niezależnie wykrywające awarie. Prawdopodobieństwo wykrycia awarii przez kolejne urządzenia wynoszą
niezależnie wykrywające awarie. Prawdopodobieństwo wykrycia awarii przez kolejne urządzenia wynoszą 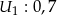 ,
, 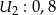 ,
, 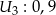 . Oblicz prawdopodobieństwo wykrycia awarii przez:
. Oblicz prawdopodobieństwo wykrycia awarii przez:
- dokładnie 2 urządzenia,
- co najmniej 1 urządzenie.
Rzucamy jednocześnie kostką i sześcioma symetrycznymi monetami. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, liczba otrzymanych oczek na kostce jest równa łącznej liczbie otrzymanych orłów na monetach.
Losujemy jedną kartę spośród wszystkich króli z talii oraz jedną kartę spośród wszystkich dam. Jakie jest prawdopodobieństwo otrzymania w ten sposób dwóch kart tego samego koloru np. dwóch treflii lub dwóch kar?
W pojemniku znajduje się 28 kul, przy czym  z nich to kule białe, a pozostałe to kule czarne. Z pojemnika losujemy dwa razy po jednej kuli ze zwracaniem. Dla jakiej liczby
z nich to kule białe, a pozostałe to kule czarne. Z pojemnika losujemy dwa razy po jednej kuli ze zwracaniem. Dla jakiej liczby  prawdopodobieństwo wylosowania jednej kuli białej i jednej czarnej jest największe?
prawdopodobieństwo wylosowania jednej kuli białej i jednej czarnej jest największe?
W jednej szufladzie znajduje się 6 czapek: 3 zielone, 2 czerwone i 1 niebieska, a w drugiej szufladzie jest 7 szalików: 2 zielone, 1 czerwony i 4 niebieskie. Wyjęto losowo jedną czapkę i jeden szalik. Oblicz prawdopodobieństwo zdarzenia A – wylosowana czapka i wylosowany szalik są tego samego koloru.
W kuchni stoją dwa koszyki. W pierwszym jest 9 papryk: 1 zielona, 4 czerwone i 4 żółte. W drugim 12 papryk: 4 zielone, 3 czerwone i 5 żółtych. Kucharz wyjmuje losowo po jednej papryce z każdego koszyka. Oblicz prawdopodobieństwo, że obie papryki będą tego samego koloru.
Ze zbioru 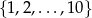 losujemy kolejno 3 liczby (mogą się powtarzać). Wyznacz prawdopodobieństwo wyboru takiej trójki
losujemy kolejno 3 liczby (mogą się powtarzać). Wyznacz prawdopodobieństwo wyboru takiej trójki 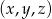 liczb, dla której
liczb, dla której 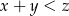 .
.
Ze zbioru cyfr 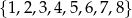 losujemy kolejno dwie cyfry (losowanie bez zwracania) i tworzymy liczby dwucyfrowe tak, że pierwsza wylosowana cyfra jest cyfrą dziesiątek, a druga – cyfrą jedności. Oblicz prawdopodobieństwo utworzenia liczby podzielnej przez 4.
losujemy kolejno dwie cyfry (losowanie bez zwracania) i tworzymy liczby dwucyfrowe tak, że pierwsza wylosowana cyfra jest cyfrą dziesiątek, a druga – cyfrą jedności. Oblicz prawdopodobieństwo utworzenia liczby podzielnej przez 4.
Ze zbioru ośmiu kolejnych liczb naturalnych – od 1 do 8 – losujemy kolejno bez zwracania dwa razy po jednej liczbie. Niech 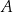 oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 8. Oblicz prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 8. Oblicz prawdopodobieństwo zdarzenia 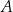 .
.
W dwóch pojemnikach znajdują się ponumerowane kule. W pierwszym pojemniku są kule z numerami: 1, 2, 3, 4, 5, w drugim z numerami: 4, 5, 6, 7, 8, 9. Losujemy po jednej kuli z każdego pojemnika i tworzymy liczbę dwucyfrową. Numer kuli wylosowanej z pierwszego pojemnika jest cyfrą dziesiątek, numer kuli wylosowanej z drugiego pojemnika jest cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że utworzona liczba jest podzielna przez 4.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych, których cyfra dziesiątek należy do zbioru 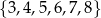 , a cyfra jedności należy do zbioru
, a cyfra jedności należy do zbioru 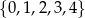 , losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 4.
, losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 4.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych, których cyfra dziesiątek należy do zbioru 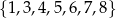 , a cyfra jedności należy do zbioru
, a cyfra jedności należy do zbioru 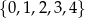 , losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 8.
, losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 8.
Mamy dwa pudełka: w pierwszym znajduje się 6 kul ponumerowanych kolejnymi liczbami od 1 do 6, a w drugim – 8 kul ponumerowanych kolejnymi liczbami od 1 do 8. Losujemy po jednej kuli z każdego pudełka i tworzymy liczbę dwucyfrową w ten sposób, że numer kuli wylosowanej z pierwszego pudełka jest cyfrą dziesiątek, a numer kuli wylosowanej z drugiego – cyfrą jedności tej liczby. Oblicz prawdopodobieństwo, że utworzona liczba jest podzielna przez 11.
Mamy dwa pudełka: w pierwszym znajduje się 6 kul ponumerowanych kolejnymi liczbami od 1 do 6, a w drugim – 7 kul ponumerowanych kolejnymi liczbami od 2 do 8. Losujemy po jednej kuli z każdego pudełka i tworzymy liczbę dwucyfrową w ten sposób, że numer kuli wylosowanej z pierwszego pudełka jest cyfrą dziesiątek, a numer kuli wylosowanej z drugiego – cyfrą jedności tej liczby. Oblicz prawdopodobieństwo, że utworzona liczba jest podzielna przez 9.
Ze zbioru ośmiu kolejnych liczb naturalnych – od 1 do 8 – losujemy kolejno bez zwracania dwa razy po jednej liczbie. Niech 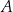 oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 12. Oblicz prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 12. Oblicz prawdopodobieństwo zdarzenia 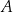 .
.
Spośród liczb naturalnych sześciocyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby, której iloczyn cyfr jest podzielny przez 9, jeżeli wiadomo, że każda cyfra wylosowanej liczby jest większa od 1?
Ze zbioru 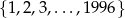 losujemy jedną liczbę. Oblicz prawdopodobieństwo, że wylosowana liczba jest podzielna przez:
losujemy jedną liczbę. Oblicz prawdopodobieństwo, że wylosowana liczba jest podzielna przez:
- 6
- 4 lub 6
- 4 lub 6 lub 10
Oblicz prawdopodobieństwo tego, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb uzyskanych oczek będzie podzielna przez 3.
Oblicz prawdopodobieństwo tego, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb uzyskanych oczek będzie podzielna przez 5.
Oblicz prawdopodobieństwo tego, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb uzyskanych oczek będzie podzielna przez 4.
W pewnym wagonie kolejowym pasażerowie siadają w sposób losowy na 54 siedzeniach, które są ustawione po trzy siedzenia w jednym rzędzie. Do wagonu wsiadło o 3 pasażerów mniej niż dostępna liczba siedzeń i dokładnie troje z tych pasażerów to mężczyźni. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że mężczyźni usiedli w jednym rzędzie i jednocześnie jeden cały rząd pozostał pusty.
Grupę 12 uczniów, wśród których jest 6 dziewczynek i 6 chłopców podzielono na 3 równoliczne grupy. Oblicz prawdopodobieństwo tego, że w każdej z utworzonych grup będzie tyle samo dziewcząt.
Ze zbioru wszystkich liczb trzycyfrowych, które są podzielne przez 7 wybieramy losowo 5 różnych liczb. Oblicz prawdopodobieństwo tego, że jedną z tych liczb jest 546, a wśród pozostałych 4 liczb jest dokładnie jedna liczba mniejsza od 546. Wynik podaj w postaci ułamka nieskracalnego.
Sześcian pomalowano, a następnie rozcięto na 1000 jednakowych sześcianików, które wrzucono do pudełka i wymieszano. Oblicz prawdopodobieństwo wylosowania z tego pudełka jednego, który:
- będzie miał dwie ściany pomalowane;
- będzie miał trzy ściany pomalowane;
- będzie miał jedną lub dwie ściany pomalowane.
W urnie znajdują się kule czarne, białe i niebieskie, przy czym są co najmniej dwie kule każdego koloru i w sumie jest 15 kul. Losujemy z urny trzy kule. Rozważmy następujące zdarzenia 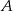 – wylosowano trzy kule tego samego koloru;
– wylosowano trzy kule tego samego koloru;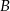 – żadne dwie z wylosowanych kul nie są tego samego koloru.
– żadne dwie z wylosowanych kul nie są tego samego koloru.
Oblicz prawdopodobieństwo zdarzenia 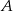 jeżeli prawdopodobieństwo zdarzenia
jeżeli prawdopodobieństwo zdarzenia 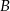 jest równe
jest równe 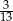 .
.

