Dany jest wzór na pole powierzchni całkowitej graniastosłupa:
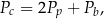
gdzie: 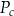 – pole powierzchni całkowitej,
– pole powierzchni całkowitej, 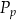 – pole podstawy,
– pole podstawy, 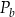 – pole powierzchni bocznej. Pole podstawy
– pole powierzchni bocznej. Pole podstawy 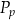 wyznaczone poprawnie z powyższego wzoru opisano równaniem
wyznaczone poprawnie z powyższego wzoru opisano równaniem
A) 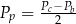 B)
B) 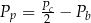 C)
C) 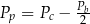 D)
D) 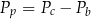

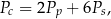
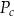 – pole powierzchni całkowitej,
– pole powierzchni całkowitej, 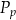 – pole podstawy,
– pole podstawy, 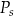 – pole powierzchni jednej ściany bocznej. Pole ściany bocznej
– pole powierzchni jednej ściany bocznej. Pole ściany bocznej 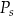 wyznaczone poprawnie z powyższego wzoru opisano równaniem
wyznaczone poprawnie z powyższego wzoru opisano równaniem 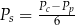
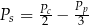
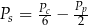
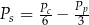
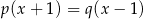 to
to 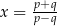 , gdy
, gdy 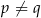
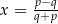 , gdy
, gdy 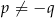
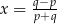 , gdy
, gdy 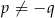
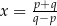 , gdy
, gdy 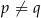
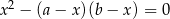 to
to 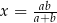 , gdy
, gdy 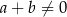
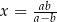 , gdy
, gdy 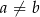
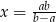 , gdy
, gdy 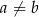
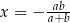 , gdy
, gdy 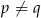
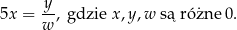
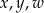 . Paweł otrzymał trzy równania:
. Paweł otrzymał trzy równania: 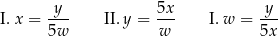
 jest równa
jest równa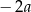
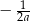
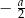
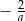
 jest równa
jest równa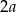
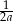
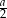
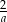
 jest równa
jest równa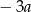
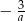
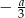
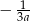
 chłopców i
chłopców i 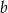 dziewczynek z klasy 5A oraz
dziewczynek z klasy 5A oraz  chłopców i
chłopców i 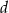 dziewczynek z klasy 6A. Ostatecznie jednak z wycieczki zrezygnowało 10% chłopców z klasy 5A oraz 6 dziewczynek z klasy 6A. Dodatkowo do wycieczki dołączyło 4 chłopców z klasy 6A i 1 dziewczynka z klasy 5A. Liczba uczniów klas 5A i 6A, którzy pojechali na wycieczkę jest równa
dziewczynek z klasy 6A. Ostatecznie jednak z wycieczki zrezygnowało 10% chłopców z klasy 5A oraz 6 dziewczynek z klasy 6A. Dodatkowo do wycieczki dołączyło 4 chłopców z klasy 6A i 1 dziewczynka z klasy 5A. Liczba uczniów klas 5A i 6A, którzy pojechali na wycieczkę jest równa 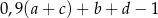
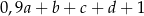
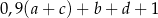
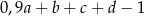
 zmniejszono o 3, a następnie do otrzymanego wyniku dodano dwukrotność liczby
zmniejszono o 3, a następnie do otrzymanego wyniku dodano dwukrotność liczby 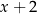 . W wyniku tych działań otrzymano wyrażenie
. W wyniku tych działań otrzymano wyrażenie 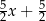
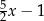
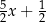
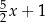
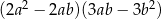 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe. 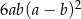 .
.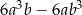 .
.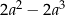 dla
dla 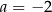 jest równa A/B.
jest równa A/B.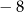
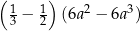 można przekształcić do postaci C/D.
można przekształcić do postaci C/D.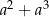
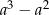
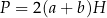 opisujący pole powierzchni bocznej graniastosłupa prostego czworokątnego o wysokości
opisujący pole powierzchni bocznej graniastosłupa prostego czworokątnego o wysokości 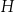 i krawędziach podstawy równych:
i krawędziach podstawy równych: 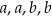 . Którym równaniem opisano
. Którym równaniem opisano 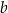 wyznaczone poprawnie z tego wzoru?
wyznaczone poprawnie z tego wzoru? 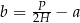
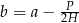
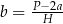
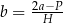
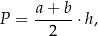
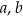 – długości podstaw trapezu,
– długości podstaw trapezu, 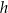 – wysokość trapezu. Długość podstawy
– wysokość trapezu. Długość podstawy  wyznaczona poprawnie z powyższego wzoru opisano równaniem
wyznaczona poprawnie z powyższego wzoru opisano równaniem 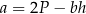
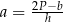
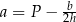
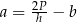
 mężczyzn i
mężczyzn i 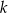 kobiet. Na przystanku wysiedli 2 mężczyźni i 3 kobiety, a wsiadło 5 mężczyzn i 2 kobiety. Gdy autobus odjechał z tego przystanku, podróżowało nim
kobiet. Na przystanku wysiedli 2 mężczyźni i 3 kobiety, a wsiadło 5 mężczyzn i 2 kobiety. Gdy autobus odjechał z tego przystanku, podróżowało nim 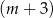 mężczyzn i
mężczyzn i 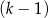 kobiet.
kobiet. 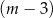 mężczyzn i
mężczyzn i 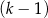 kobiet.
kobiet. 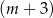 mężczyzn i
mężczyzn i 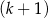 kobiet.
kobiet. 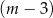 mężczyzn i
mężczyzn i 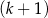 kobiet.
kobiet. 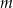 mężczyzn i
mężczyzn i 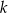 kobiet. Na drugim piętrze wysiadło 3 mężczyzn i 4 kobiety, a wsiadło 2 mężczyzn i 3 kobiety. Gdy winda odjechała z drugiego piętra, znajdowało się w niej
kobiet. Na drugim piętrze wysiadło 3 mężczyzn i 4 kobiety, a wsiadło 2 mężczyzn i 3 kobiety. Gdy winda odjechała z drugiego piętra, znajdowało się w niej 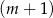 mężczyzn i
mężczyzn i 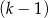 kobiet.
kobiet. 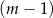 mężczyzn i
mężczyzn i 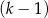 kobiet.
kobiet. 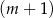 mężczyzn i
mężczyzn i 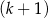 kobiet.
kobiet. 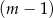 mężczyzn i
mężczyzn i 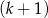 kobiet.
kobiet.  złotych, a 5 kilogramów ziemniaków kosztuje
złotych, a 5 kilogramów ziemniaków kosztuje 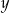 złotych, to
złotych, to 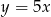
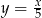
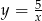
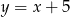
 złotych, a za 5 zł kupiono
złotych, a za 5 zł kupiono 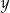 kg ziemniaków, to
kg ziemniaków, to 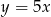
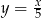
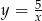
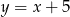
 jest o 8 większa od potrojonego kwadratu liczby
jest o 8 większa od potrojonego kwadratu liczby  ” zapisane w postaci równania to
” zapisane w postaci równania to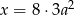
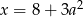
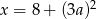
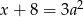
 jest 3 razy większa od połowy sześcianu liczby
jest 3 razy większa od połowy sześcianu liczby 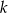 ” zapisane w postaci równania to
” zapisane w postaci równania to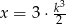
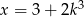
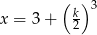
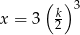
 jest o 5 mniejsza od podwojonego kwadratu liczby
jest o 5 mniejsza od podwojonego kwadratu liczby 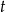 ” zapisane w postaci równania to
” zapisane w postaci równania to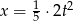
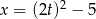
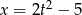
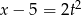
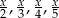 jest równa
jest równa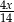
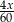
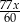
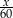

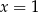 oraz dla
oraz dla 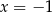 . Które to wyrażenie?
. Które to wyrażenie? 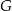
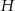
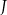
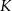

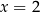 oraz dla
oraz dla 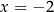 . Które to wyrażenie?
. Które to wyrażenie? 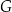
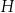
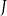
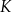

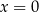 oraz dla
oraz dla 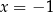 . Które to wyrażenie?
. Które to wyrażenie? 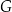
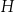
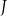
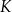
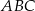 :
: 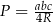 , gdzie
, gdzie 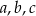 są długościami boków tego trójkąta, a
są długościami boków tego trójkąta, a 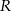 jest promieniem okręgu przechodzącego przez punkty
jest promieniem okręgu przechodzącego przez punkty 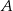 ,
, 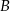 i
i 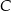 . Promień
. Promień 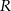 można wyrazić wzorem A/B.
można wyrazić wzorem A/B.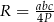
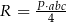
 trójkąta
trójkąta 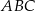 można wyrazić wzorem C/D.
można wyrazić wzorem C/D.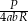
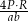
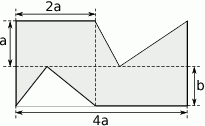
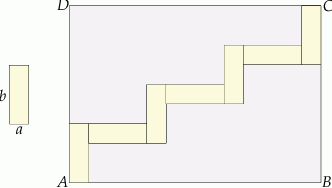
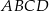 . Wzór ten składa się z 7 prostokątów o bokach
. Wzór ten składa się z 7 prostokątów o bokach  i
i 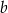 .
. 
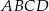 jest równe
jest równe 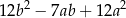
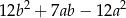
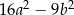
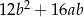
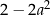 dla
dla 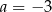 jest równa A/B.
jest równa A/B.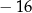
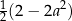 można przekształcić do postaci C/D.
można przekształcić do postaci C/D.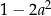
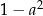
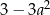 dla
dla 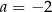 jest równa A/B.
jest równa A/B.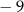
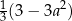 można przekształcić do postaci C/D.
można przekształcić do postaci C/D.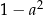
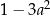
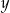 z równania
z równania 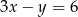 otrzymujemy:
otrzymujemy: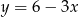
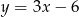
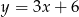
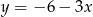
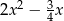 dla
dla 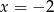 jest liczba:
jest liczba: