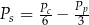Wyrażenie 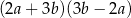 jest równe
jest równe
A) 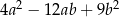 B)
B) 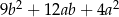 C)
C) 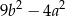 D)
D) 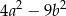
/Szkoła podstawowa/Zadania testowe/Wyrażenia algebraiczne
Wyrażenie 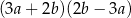 jest równe
jest równe
A) 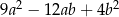 B)
B) 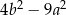 C)
C) 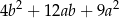 D)
D) 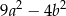
Suma liczby odwrotnej do 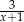 i przeciwnej do
i przeciwnej do 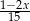 jest równa
jest równa
A) 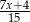 B)
B) 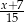 C)
C) 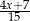 D)
D) 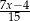
W naczyniu znajdowało się 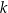 litrów wody. Marcin odlał z tego naczynia
litrów wody. Marcin odlał z tego naczynia 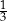 tej objętości wody, a następnie Magda odlała 3 litry wody. Objętość wody wyrażoną w litrach, która pozostała w naczyniu, opisuje wyrażenie
tej objętości wody, a następnie Magda odlała 3 litry wody. Objętość wody wyrażoną w litrach, która pozostała w naczyniu, opisuje wyrażenie
A) 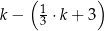 B)
B) 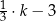 C)
C) 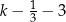 D)
D) 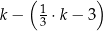
Sprzedawca kupił do swojego sklepu 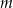 kilogramów marchwi i
kilogramów marchwi i 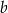 kilogramów buraków: zapłacił po 1,50 zł za kilogram marchwi i po 0,90 zł za kilogram buraków. Warzywa te sprzedał za łączną kwotę 180 złotych. Które wyrażenie przedstawia różnicę kwoty uzyskanej za sprzedane warzywa i kosztu ich zakupu?
kilogramów buraków: zapłacił po 1,50 zł za kilogram marchwi i po 0,90 zł za kilogram buraków. Warzywa te sprzedał za łączną kwotę 180 złotych. Które wyrażenie przedstawia różnicę kwoty uzyskanej za sprzedane warzywa i kosztu ich zakupu?
A) 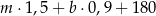 B)
B) 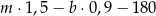
C) 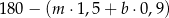 D)
D) 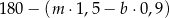
Sprzedawca sprzedał w swoim sklepie 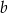 kilogramów bananów i
kilogramów bananów i 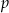 kilogramów pomarańczy: banany sprzedawał po 3,50 zł za kilogram, a pomarańcze po 2,80 zł za kilogram. Na zakup tych warzyw sprzedawca wydał 240 zł. Które wyrażenie przedstawia różnicę kwoty uzyskanej za sprzedane warzywa i kosztu ich zakupu?
kilogramów pomarańczy: banany sprzedawał po 3,50 zł za kilogram, a pomarańcze po 2,80 zł za kilogram. Na zakup tych warzyw sprzedawca wydał 240 zł. Które wyrażenie przedstawia różnicę kwoty uzyskanej za sprzedane warzywa i kosztu ich zakupu?
A) 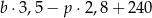 B)
B) 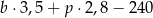
C) 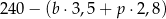 D)
D) 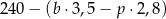
Właściciel sklepu przemysłowego kupił  opakowań 5-kilogramowego proszku do prania w cenie
opakowań 5-kilogramowego proszku do prania w cenie  złotych za kilogram. Zakupiony proszek sprzedał za łączną kwotę 3200 zł. Od uzyskanego przychodu, czyli od różnicy między kwotą uzyskaną ze sprzedaży i kosztami zakupu musi zapłacić podatek dochodowy w wysokości 19%. Które wyrażenie przedstawia wysokość podatku jaki musi zapłacić właściciel tego sklepu?
złotych za kilogram. Zakupiony proszek sprzedał za łączną kwotę 3200 zł. Od uzyskanego przychodu, czyli od różnicy między kwotą uzyskaną ze sprzedaży i kosztami zakupu musi zapłacić podatek dochodowy w wysokości 19%. Które wyrażenie przedstawia wysokość podatku jaki musi zapłacić właściciel tego sklepu?
A) 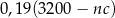 B)
B) 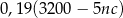
C) 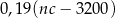 D)
D) 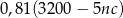
Sprzedawca kupił od ogrodnika róże i tulipany za łączną kwotę 580 zł. Jeden tulipan kosztował 1,20 zł, a cena jednej róży była równa 4 zł. Sprzedawca kupił o 50 tulipanów więcej niż róż. Jeśli liczbę zakupionych tulipanów oznaczymy przez 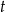 , to podane zależności opisuje równanie
, to podane zależności opisuje równanie
A) 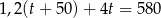 B)
B) 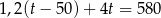
C) 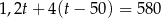 D)
D) 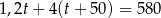
Po wykonaniu działań w wyrażeniu 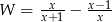 otrzymujemy
otrzymujemy
A) 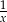 B)
B) 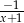 C)
C) 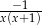 D)
D) 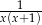
Wyrażenie 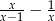 , określone dla
, określone dla 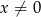 i
i 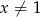 , jest równe
, jest równe
A) 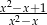 B)
B) 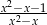 C)
C) 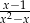 D)
D) 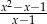
Po wykonaniu działań w wyrażeniu 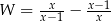 otrzymujemy
otrzymujemy
A) 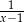 B)
B) 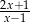 C)
C) 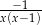 D)
D) 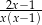
Wyrażenie 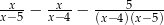 można zapisać w postaci
można zapisać w postaci
A) 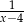 B)
B) 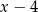 C)
C) 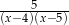 D)
D) 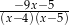
Wyrażenie 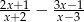 jest równe
jest równe
A) 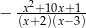 B)
B) 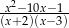 C)
C) 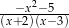 D)
D) 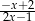
Wyrażenie 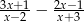 jest równe
jest równe
A) 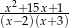 B)
B) 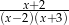 C)
C) 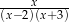 D)
D) 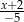
Po wykonaniu działania 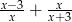 otrzymujemy
otrzymujemy
A) 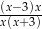 B)
B) 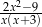 C)
C) 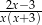 D)
D) 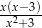
Jacek ma o 4 lata młodszego brata Kamila, który ma  lat. Kamil ma koleżankę Basię, która jest od niego dwa razy starsza. Różnica wieku Basi i Jacka jest równa
lat. Kamil ma koleżankę Basię, która jest od niego dwa razy starsza. Różnica wieku Basi i Jacka jest równa
A) 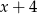 B)
B) 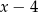 C)
C)  D)
D) 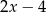
Po skróceniu wyrażenia 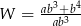 otrzymamy
otrzymamy
A) 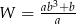 B)
B) 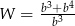 C)
C) 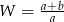 D)
D) 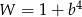
Po skróceniu wyrażenia 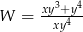 otrzymamy
otrzymamy
A) 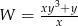 B)
B) 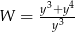 C)
C) 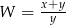 D)
D) 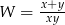
Po skróceniu wyrażenia 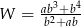 otrzymamy
otrzymamy
A) 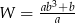 B)
B) 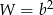 C)
C) 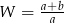 D)
D) 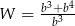
Tomek otrzymał torebkę, w której było  cukierków. Sam zjadł z tej torebki 8 cukierków, a pozostałe cukierki rozdzielił pomiędzy swoich 5 kolegów. Czworo z tych chłopców otrzymało tyle samo cukierków, a piąty z nich, Szymon, otrzymał o jeden cukierek więcej od pozostałych. Liczba cukierków, które otrzymał Szymon jest równa
cukierków. Sam zjadł z tej torebki 8 cukierków, a pozostałe cukierki rozdzielił pomiędzy swoich 5 kolegów. Czworo z tych chłopców otrzymało tyle samo cukierków, a piąty z nich, Szymon, otrzymał o jeden cukierek więcej od pozostałych. Liczba cukierków, które otrzymał Szymon jest równa
A) 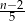 B)
B) 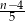 C)
C) 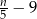 D)
D) 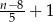
Iloczyn 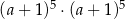 jest równy
jest równy
A) 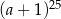 B)
B) 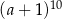 C)
C) 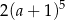 D)
D) 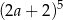
Liczbę  powiększono o 7, a następnie otrzymany wynik zwiększono 4–krotnie. Liczbę
powiększono o 7, a następnie otrzymany wynik zwiększono 4–krotnie. Liczbę 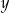 zwiększono 5–krotnie, a otrzymany wynik powiększono o 3. Która para wyrażeń algebraicznych poprawnie opisuje wykonane działania?
zwiększono 5–krotnie, a otrzymany wynik powiększono o 3. Która para wyrażeń algebraicznych poprawnie opisuje wykonane działania?
A) 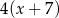 oraz
oraz 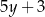 B)
B) 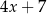 oraz
oraz 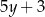
C) 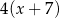 oraz
oraz 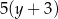 D)
D) 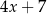 oraz
oraz 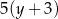
Liczbę  powiększono o 3, a następnie otrzymany wynik zwiększono 7–krotnie. Liczbę
powiększono o 3, a następnie otrzymany wynik zwiększono 7–krotnie. Liczbę 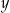 zwiększono 3–krotnie, a otrzymany wynik powiększono o 4. Która para wyrażeń algebraicznych poprawnie opisuje wykonane działania?
zwiększono 3–krotnie, a otrzymany wynik powiększono o 4. Która para wyrażeń algebraicznych poprawnie opisuje wykonane działania?
A) 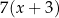 oraz
oraz 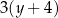 B)
B) 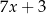 oraz
oraz 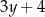
C) 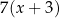 oraz
oraz 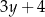 D)
D) 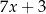 oraz
oraz 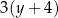
Liczba  jest ujemna, a liczba
jest ujemna, a liczba 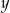 jest dodatnia. Wartość ujemną przyjmuje wyrażenie
jest dodatnia. Wartość ujemną przyjmuje wyrażenie
A) 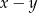 B)
B) 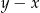 C)
C) 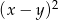 D)
D) 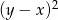
Liczba  jest ujemna, a liczba
jest ujemna, a liczba 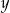 jest dodatnia. Wartość ujemną przyjmuje wyrażenie
jest dodatnia. Wartość ujemną przyjmuje wyrażenie
A) 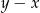 B)
B) 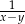 C)
C) 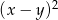 D)
D) 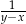
Liczba  jest dodatnia, a liczba
jest dodatnia, a liczba 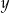 jest ujemna. Wartość ujemną przyjmuje wyrażenie
jest ujemna. Wartość ujemną przyjmuje wyrażenie
A) 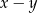 B)
B) 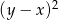 C)
C) 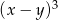 D)
D) 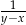
Liczba  jest ujemna, a liczba
jest ujemna, a liczba 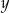 jest dodatnia. Wartość dodatnią przyjmuje wyrażenie
jest dodatnia. Wartość dodatnią przyjmuje wyrażenie
A) 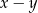 B)
B) 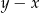 C)
C) 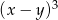 D)
D) 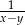
Sześcian wyrażenia 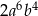 jest równy
jest równy
A) 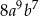 B)
B) 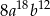 C)
C) 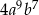 D)
D) 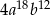
Kwadrat wyrażenia 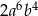 jest równy
jest równy
A) 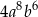 B)
B) 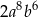 C)
C) 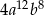 D)
D) 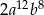
Sześcian wyrażenia 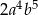 jest równy
jest równy
A) 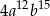 B)
B) 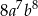 C)
C) 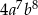 D)
D) 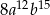
Wyrażenie 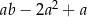 można przekształcić do postaci
można przekształcić do postaci
A) 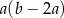 B)
B) 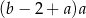 C)
C) 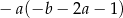 D)
D) 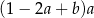
W pudełku są kulki czerwone, zielone i niebieskie. Kulek czerwonych jest trzy razy więcej niż zielonych i o dwie mniej niż niebieskich. W pudełku najmniej jest kulek A/B.
A) niebieskich B) zielonych
Jeśli liczbę kulek zielonych oznaczymy przez  , to liczbę wszystkich kulek w pudełku opisuje wyrażenie C/D.
, to liczbę wszystkich kulek w pudełku opisuje wyrażenie C/D.
C) 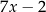 D)
D) 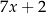
Dany jest wzór opisujący pole trapezu: 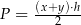 , gdzie
, gdzie  i
i 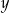 oznaczają długości podstaw trapezu, a
oznaczają długości podstaw trapezu, a 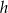 oznacza wysokość trapezu. Którym równaniem opisano
oznacza wysokość trapezu. Którym równaniem opisano  wyznaczone poprawnie z tego wzoru?
wyznaczone poprawnie z tego wzoru?
A) 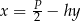 B)
B) 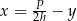 C)
C) 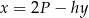 D)
D) 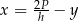
Zdanie „różnica kwadratów dwóch kolejnych liczb naturalnych nieparzystych jest niemniejsza niż 5” przedstawiono w postaci nierówności:
A) 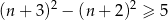 B)
B) 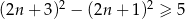
C) 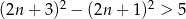 D)
D) ![2 [(2n + 3) − (2n + 1 )] ≥ 5](https://img.zadania.info/zad/3694791/HzadT3x.gif)
Zdanie „kwadrat różnicy dwóch kolejnych liczb naturalnych nieparzystych jest niemniejszy niż 5” można zapisać w postaci nierówności:
A) ![[(n + 3) − (n + 2)]2 ≥ 5](https://img.zadania.info/zad/5555770/HzadT0x.gif) B)
B) 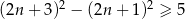
C) 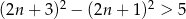 D)
D) ![2 [(2n + 3) − (2n + 1 )] ≥ 5](https://img.zadania.info/zad/5555770/HzadT3x.gif)
Jeśli 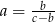 , to
, to
A) 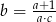 B)
B) 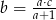 C)
C) 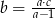 D)
D) 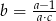
Jeśli 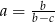 , to
, to
A) 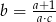 B)
B) 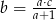 C)
C) 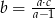 D)
D) 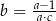
Dane są trzy wyrażenia:
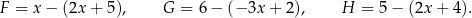
Dla każdej wartości  prawdziwa jest równość
prawdziwa jest równość
A) 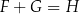 B)
B) 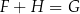 C)
C) 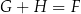 D)
D) 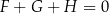
Jeżeli 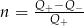 i
i 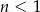 to
to
A) 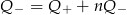 B)
B) 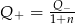 C)
C) 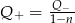 D)
D) 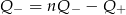
Jeżeli 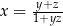 i
i 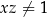 , to
, to
A) 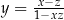 B)
B) 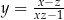 C)
C) 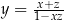 D)
D) 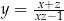
Dany jest wzór na pole powierzchni całkowitej graniastosłupa:
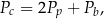
gdzie: 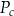 – pole powierzchni całkowitej,
– pole powierzchni całkowitej, 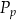 – pole podstawy,
– pole podstawy, 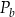 – pole powierzchni bocznej. Pole podstawy
– pole powierzchni bocznej. Pole podstawy 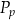 wyznaczone poprawnie z powyższego wzoru opisano równaniem
wyznaczone poprawnie z powyższego wzoru opisano równaniem
A) 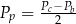 B)
B) 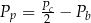 C)
C) 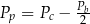 D)
D) 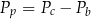
Dany jest wzór na pole powierzchni całkowitej graniastosłupa prawidłowego sześciokątnego:
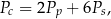
gdzie: 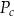 – pole powierzchni całkowitej,
– pole powierzchni całkowitej, 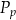 – pole podstawy,
– pole podstawy, 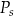 – pole powierzchni jednej ściany bocznej. Pole ściany bocznej
– pole powierzchni jednej ściany bocznej. Pole ściany bocznej 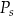 wyznaczone poprawnie z powyższego wzoru opisano równaniem
wyznaczone poprawnie z powyższego wzoru opisano równaniem
A) 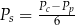 B)
B) 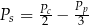 C)
C) 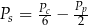 D)
D)