Sześcian/Stereometria/Geometria - zadania z matematyki

/Szkoła średnia/Geometria/Stereometria/Sześcian

Po wydłużeniu każdej krawędzi sześcianu o 2, długość jego przekątnej podwoiła się. Oblicz pole powierzchni całkowitej powiększonego sześcianu.

Odległość wierzchołka sześcianu od przekątnej sześcianu (do której dany wierzchołek nie należy) jest równa 4 cm. Oblicz objętość sześcianu.

Mrówka przeszła po powierzchni sześcianu z wierzchołka 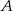do wierzchołka będącego drugim końcem przekątnej sześcianu wychodzącej z wierzchołka 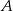, przy czym była to droga najkrótsza. Narysuj siatkę sześcianu i oblicz odległość, jaką pokonała mrówka, jeżeli krawędź sześcianu ma długość √ -- 5 .

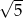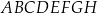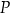Dany jest sześcian ABCDEF GH o krawędzi długości . Punkt jest środkiem krawędzi 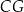tego sześcianu.

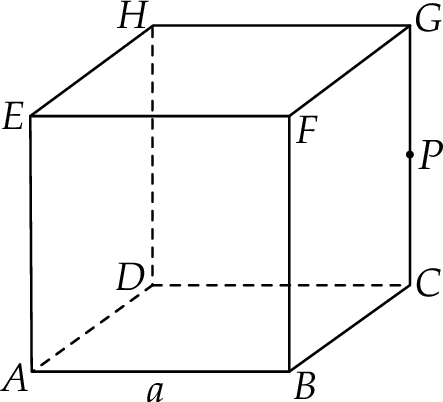
ZINFO-FIGURE

Oblicz odległość wierzchołka 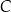od płaszczyzny zawierającej punkty 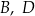B , D oraz .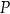

Przekątna sześcianu ma długość 9. Oblicz pole powierzchni całkowitej tego sześcianu.

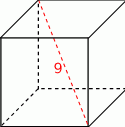
Wykaż, że w sześcianie, odległość krawędzi od nieprzecinającej się z nią przekątnej sześcianu jest równa połowie długości przekątnej ściany.

Przez środek jednej krawędzi podstawy sześcianu, koniec przeciwległej krawędzi tej podstawy oraz środek krawędzi bocznej, poprowadzono płaszczyznę. Opisz ﬁgurę, którą otrzymamy w wyniku tego przekroju. Rozważ 2 przypadki.

Do sześciennego pudła o boku długości 60 cm, włożono walec, który jest styczny do przylegających ścian. Jak dużą kulkę można jeszcze zmieścić w wolnym rogu pudła?

Przekątna sześcianu jest o 3 dłuższa od krawędzi sześcianu. Oblicz objętość tego sześcianu.

Ukryj Podobne zadania

Długość krawędzi sześcianu jest o 2 krótsza od długości jego przekątnej. Oblicz długość przekątnej tego sześcianu.

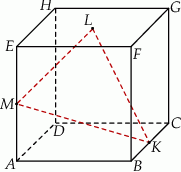
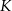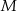Punkty i są środkami krawędz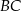i i 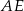sześcianu 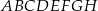ABCDEF GH o krawędzi długości 1. Punkt 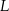jest środkiem ściany 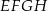EF GH (zobacz rysunek). Oblicz obwód trójkąta KLM .

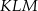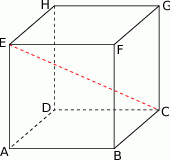
Dany jest sześcian 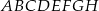ABCDEF GH , w którym 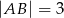|AB | = 3 (patrz rysunek). Oblicz odległość wierzchołka 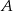od przekątnej .

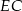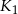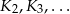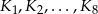Niech będzie sześcianem o krawędzi długości . Konstruujemy kolejno sześciany K2,K 3,... takie, że pole powierzchni całkowitej kolejnego sześcianu jest dwa razy większe od pola powierzchni poprzedniego sześcianu. Oblicz sumę objętości sześcianów K ,K ,...,K 1 2 8 .

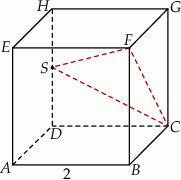
Dany jest sześcian 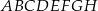ABCDEF GH o krawędzi długości 2. Punkt 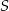jest środkiem krawędzi 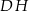(zobacz rysunek). Oblicz miarę najmniejszego kąta wewnętrznego trójkąta CF S .

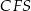Punkty 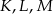K ,L,M i 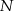są środkami krawędzi 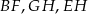BF ,GH ,EH i 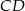prostopadłościanu 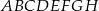ABCDEF GH , w którym 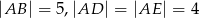|AB | = 5,|AD | = |AE | = 4 . Uzasadnij, że |KL | = |MN | .

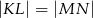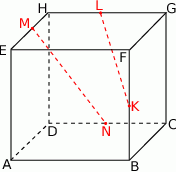
Dany jest sześcian 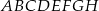ABCDEF GH . Przez wierzchołk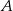i i 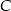oraz środek 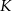krawędzi 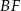poprowadzono płaszczyznę, która przecina przekątną 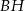w punkcie 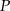(zobacz rysunek).

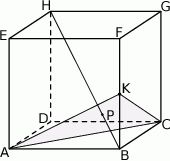
Wykaż, że 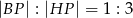|BP | : |HP | = 1 : 3 .

Ukryj Podobne zadania

Dany jest sześcian 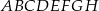ABCDEF GH . Przez wierzchołki 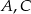A,C oraz 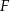poprowadzono płaszczyznę, która przecina przekątną 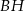w punkcie 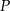(zobacz rysunek).

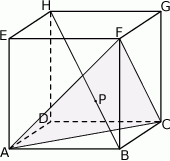
Wykaż, że 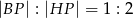|BP | : |HP | = 1 : 2 .

Punkty 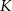i 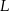są środkami krawędz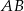i i 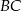sześcianu 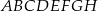ABCDEF GH o krawędzi długości 1. Punkt 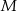jest środkiem ściany 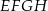EFGH (zobacz rysunek). Oblicz pole trójkąta KLM .

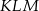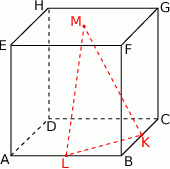
W sześcianie o krawędzi długości 2 połączono ze sobą środki trzech ścian mających wspólny wierzchołek. Sporządź odpowiedni rysunek i oblicz pole otrzymanego trójkąta.

Oblicz pole powierzchni i objętość sześcianu, którego przekątna ma długość 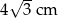√ -- 4 3 cm .

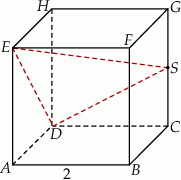
Dany jest sześcian 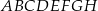ABCDEF GH o krawędzi długości 2. Punkt 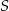jest środkiem krawędzi 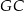(zobacz rysunek). Oblicz promień okręgu opisanego na trójkącie EDS .

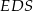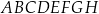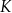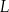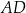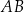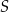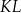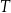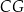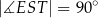Dany jest sześcian ABCDEF GH o krawędzi długości 1. Punkty i są środkami odpowiednio krawędzi i , a punkt jest środkiem odcinka . Punkt jest takim punktem krawędzi , że |∡EST | = 90∘ (zobacz rysunek).

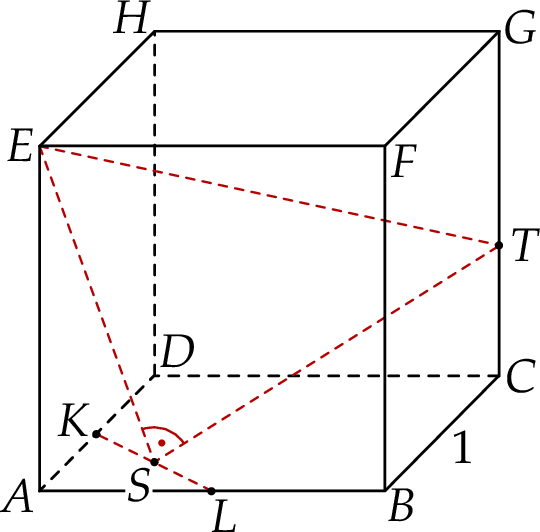
ZINFO-FIGURE

Oblicz odległość punktu 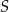od środka odcinka .

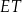Strona 1 z 2