Krawędź sześcianu ma długość  . Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez przekątną podstawy i środki dwóch kolejnych krawędzi górnej podstawy.
. Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez przekątną podstawy i środki dwóch kolejnych krawędzi górnej podstawy.
/Szkoła średnia/Geometria/Stereometria/Sześcian
W sześcian o krawędzi 4 wpisano kulę styczną do trzech ścian sześcianu oraz przechodzącą przez środek sześcianu. Oblicz promień tej kuli.
Krawędź sześcianu jest o 4 krótsza od jego przekątnej. Oblicz pole powierzchni całkowitej tego sześcianu.
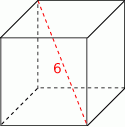
Przekątna sześcianu ma długość 6. Oblicz objętość tego sześcianu.
Sześcian przecięto płaszczyzną przechodzącą przez przekątną podstawy. Płaszczyzna ta tworzy z podstawą kąt  . Dla jakich wartości
. Dla jakich wartości 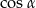 otrzymany przekrój jest trójkątem?
otrzymany przekrój jest trójkątem?
Punkty 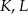 i
i 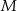 są środkami krawędzi
są środkami krawędzi 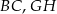 i
i 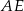 sześcianu
sześcianu 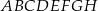 o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta
o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta 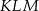 .
.
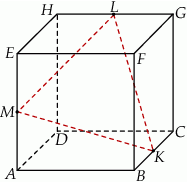
Na krawędziach sześcianu 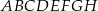 zaznaczono punkty
zaznaczono punkty 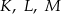 tak, że każdy z nich jest środkiem odpowiedniej krawędzi (patrz rysunek). Oblicz pole trójkąta
tak, że każdy z nich jest środkiem odpowiedniej krawędzi (patrz rysunek). Oblicz pole trójkąta 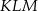 , jeśli krawędź sześcianu ma długość równą 4.
, jeśli krawędź sześcianu ma długość równą 4.
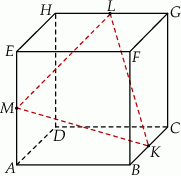
Na krawędziach sześcianu 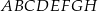 zaznaczono punkty
zaznaczono punkty 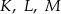 tak, że każdy z nich jest środkiem odpowiedniej krawędzi (patrz rysunek). Oblicz pole trójkąta
tak, że każdy z nich jest środkiem odpowiedniej krawędzi (patrz rysunek). Oblicz pole trójkąta 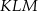 , jeśli krawędź sześcianu ma długość równą 2.
, jeśli krawędź sześcianu ma długość równą 2.
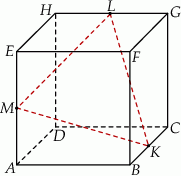
Punkty 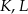 i
i 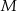 są środkami krawędzi
są środkami krawędzi 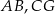 i
i 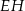 sześcianu
sześcianu 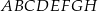 o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta
o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta 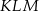 .
.
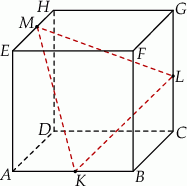
Oblicz sinus kąta między przekątną sześcianu a jego płaszczyzną podstawy.
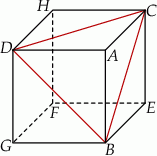
W narysowanym obok sześcianie krawędź ma długość  . Oblicz odległość wierzchołka
. Oblicz odległość wierzchołka 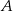 od płaszczyzny przechodzącej przez wierzchołki
od płaszczyzny przechodzącej przez wierzchołki 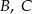 i
i 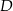 .
.
Punkty 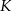 i
i 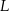 są środkami odpowiednio podstawy
są środkami odpowiednio podstawy 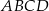 i krawędzi
i krawędzi 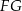 sześcianu
sześcianu 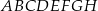 . Suma kwadratów długości odcinków
. Suma kwadratów długości odcinków 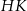 i
i 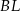 jest równa 33. Oblicz pole powierzchni całkowitej sześcianu.
jest równa 33. Oblicz pole powierzchni całkowitej sześcianu.
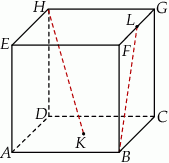
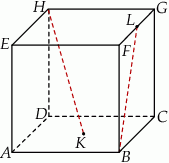
Punkty 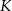 i
i 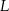 są środkami odpowiednio podstawy
są środkami odpowiednio podstawy 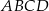 i krawędzi
i krawędzi 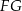 sześcianu
sześcianu 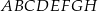 . Suma kwadratów długości odcinków
. Suma kwadratów długości odcinków 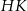 i
i 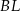 jest równa 44. Oblicz objętość tego sześcianu.
jest równa 44. Oblicz objętość tego sześcianu.
Sześcian o krawędzi  przecięto płaszczyzną przechodzącą przez przekątną podstawy, która jest nachylona do płaszczyzny podstawy pod kątem
przecięto płaszczyzną przechodzącą przez przekątną podstawy, która jest nachylona do płaszczyzny podstawy pod kątem 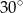 . Oblicz pole powstałego przekroju.
. Oblicz pole powstałego przekroju.
Z jednakowych sześciennych kostek, których krawędź ma długość 1, sklejono bryłę przedstawioną na rysunku.
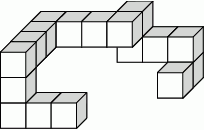
Ile kostek należy dokleić do tej bryły, aby otrzymać wypełniony kostkami sześcian?
Przez środki trzech różnych krawędzi sześcianu 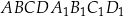 wychodzących z wierzchołka
wychodzących z wierzchołka 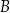 poprowadzono płaszczyznę, która wyznaczyła przekrój bryły – trójkąt
poprowadzono płaszczyznę, która wyznaczyła przekrój bryły – trójkąt 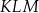 . Oblicz odległość wierzchołka
. Oblicz odległość wierzchołka 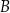 od tego przekroju, jeżeli wiadomo, że długość krawędzi sześcianu wynosi 8.
od tego przekroju, jeżeli wiadomo, że długość krawędzi sześcianu wynosi 8.
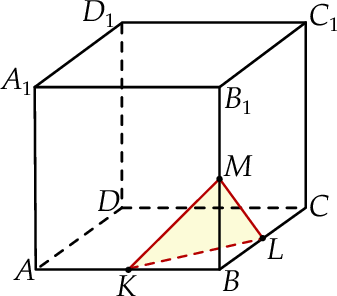
Narysuj przekrój równoległościanu płaszczyzną 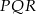 .
.
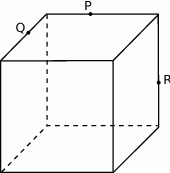
Na narysowanej poniżej siatce sześcianu zaznaczono trzy środki ścian sześcianu.
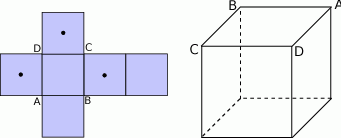
- Zaznacz na powierzchni sześcianu trzy punkty
 odpowiadające środkom ścian wskazanym na jego siatce.
odpowiadające środkom ścian wskazanym na jego siatce. - Wiedząc, że krawędź sześcianu ma długość 1, oblicz pole trójkąta
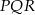 .
.
Płaszczyzna 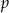 jest styczna do kuli wpisanej w sześcian
jest styczna do kuli wpisanej w sześcian 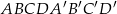 o krawędzi długości
o krawędzi długości 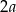 oraz przecina krawędzie
oraz przecina krawędzie 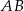 ,
, 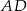 i
i 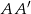 w takich punktach
w takich punktach 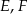 i
i 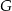 odpowiednio, że
odpowiednio, że 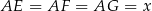 . Wykonaj odpowiedni rysunek i wyznacz
. Wykonaj odpowiedni rysunek i wyznacz  .
.
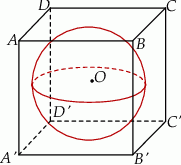
Oblicz odległość środka ściany sześcianu o krawędzi długości  od przekątnej tego sześcianu.
od przekątnej tego sześcianu.
Dany jest sześcian 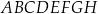 o krawędzi długości 6. Punkt
o krawędzi długości 6. Punkt 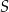 jest punktem przecięcia przekątnych
jest punktem przecięcia przekątnych 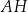 i
i 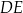 ściany bocznej
ściany bocznej 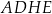 (zobacz rysunek).
(zobacz rysunek).
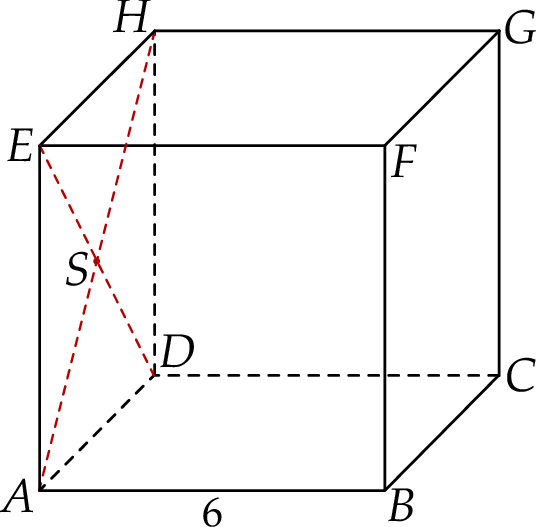
Oblicz wysokość trójkąta 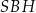 poprowadzoną z punktu
poprowadzoną z punktu 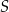 na bok
na bok 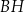 tego trójkąta.
tego trójkąta.
Dany jest sześcian 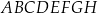 o krawędzi długości 3. Punkt
o krawędzi długości 3. Punkt 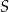 jest punktem przecięcia przekątnych
jest punktem przecięcia przekątnych 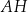 i
i 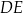 ściany bocznej
ściany bocznej 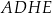 (zobacz rysunek).
(zobacz rysunek).
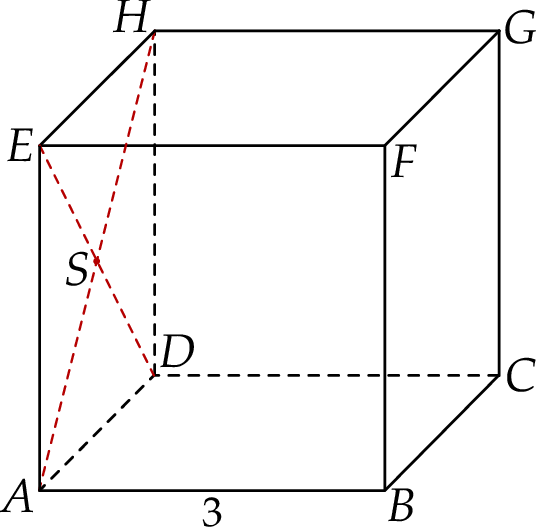
Oblicz wysokość trójkąta 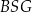 poprowadzoną z punktu
poprowadzoną z punktu 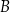 na bok
na bok 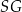 tego trójkąta.
tego trójkąta.
Wykaż, że objętość sześcianu jest sześć razy większa od objętości ośmiościanu foremnego, wyznaczonego przez środki ścian tego sześcianu.
Sześcian 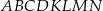 przecięto płaszczyzną przechodzącą przez przekątną
przecięto płaszczyzną przechodzącą przez przekątną 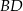 podstawy, która jest nachylona do płaszczyzny podstawy pod kątem
podstawy, która jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 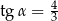 (zobacz rysunek).
(zobacz rysunek).
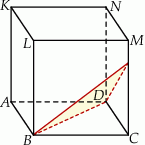
Odległość wierzchołka 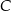 od płaszczyzny tego przekroju jest równa 6. Oblicz objętość sześcianu
od płaszczyzny tego przekroju jest równa 6. Oblicz objętość sześcianu 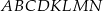 .
.
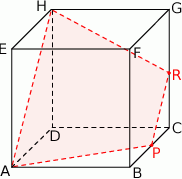
Dany jest sześcian 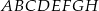 o krawędzi długości 2. Punkt
o krawędzi długości 2. Punkt 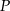 jest środkiem krawędzi
jest środkiem krawędzi 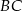 . Płaszczyzna
. Płaszczyzna 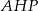 przecina krawędź
przecina krawędź 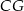 w punkcie
w punkcie 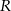 (zobacz rysunek). Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez punkty
(zobacz rysunek). Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez punkty 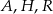 i
i 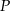 .
.
Jacek bawi się sześciennymi klockami o krawędzi 2 cm. Zbudował z nich jeden duży sześcian o krawędzi 8 cm i wykorzystał do tego wszystkie swoje klocki. Następnie zburzył budowlę i ułożył z tych klocków drugą bryłę – graniastosłup prawidłowy czworokątny. Wtedy okazało się, że został mu dokładnie jeden klocek, którego nie było gdzie dołożyć. Oblicz stosunek pola powierzchni całkowitej pierwszej ułożonej bryły do pola powierzchni całkowitej drugiej bryły i wynik podaj w postaci ułamka nieskracalnego.
Ania bawi się sześciennymi klockami o krawędzi 2 cm i buduje z nich bryły w kształcie prostokątów (prostopadłościanów o wysokości 1 klocka) w sposób przedstawiony na poniższym rysunku.
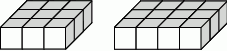
Najpierw Ania zbudowała z klocków pełen kwadrat o krawędzi 36 cm i wykorzystała do tego wszystkie swoje klocki. Następnie zburzyła tę budowlę i ułożyła z tych klocków prostokąt. Wtedy okazało się, że został jej dokładnie jeden klocek, którego nie było gdzie dołożyć. Oblicz stosunek pola powierzchni całkowitej pierwszej z ułożonych figur do pola powierzchni całkowitej drugiej figury.

